北京化工大学2010—2011学年第二学期 《微积分(II)》期末考试试卷 课程代码MAT14700T 班级 姓名: 学号: 分数: 题号 2 6 10总分 得分 小计算,业,们由:=F+,,2所围成的闭区域。 e 1
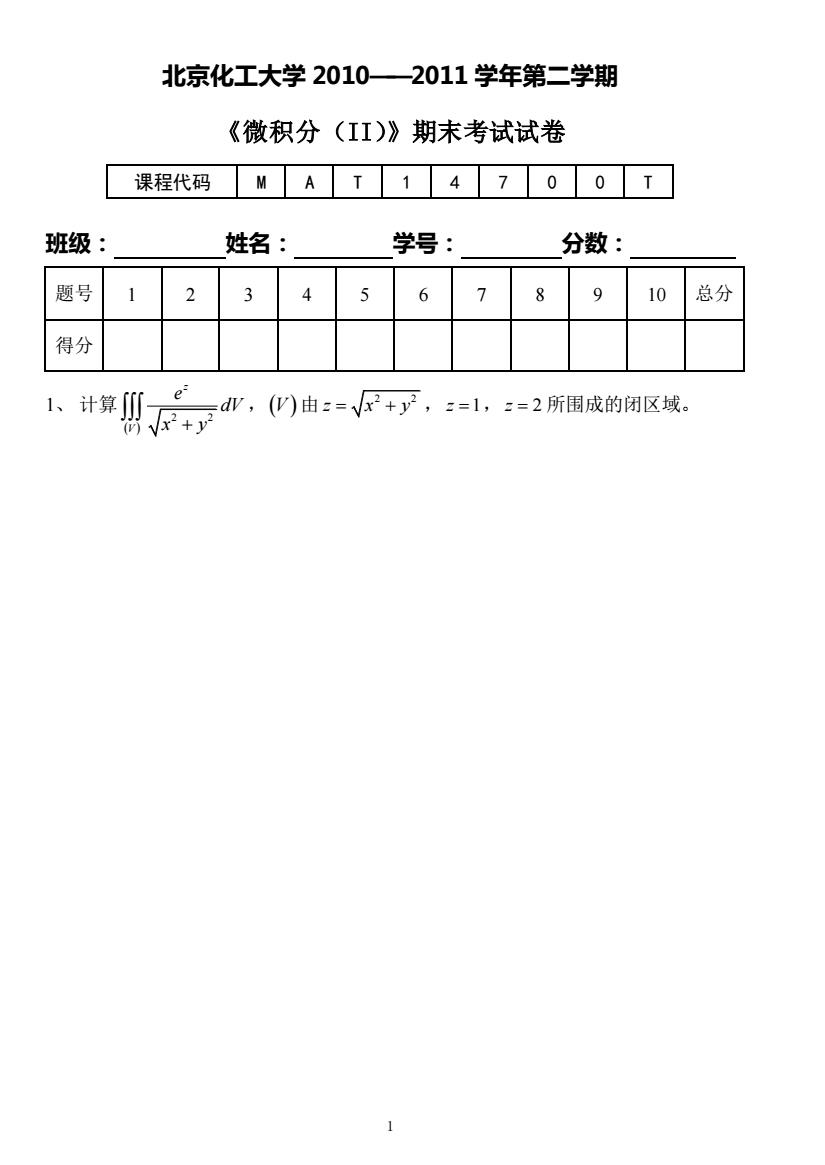
1 北京化工大学 2010——2011 学年第二学期 《微积分(II)》期末考试试卷 课程代码 M A T 1 4 7 0 0 T 班级: 姓名: 学号: 分数: 题号 1 2 3 4 5 6 7 8 9 10 总分 得分 1、 计算 ( ) 2 2 z V e dV x y + ,(V ) 由 2 2 z x y = + , z =1, z = 2 所围成的闭区域

2、计算d,(C)为球面x2+y2+z2=2与平面x=y的交线。 ( 2
2 2、 计算 (C) y ds ,(C) 为球面 2 2 2 x y z + + = 2 与平面 x y = 的交线

3、计算肌2x++小西,()为平面+皆+1,(≥0,20:≥0. 3
3 3、 计算 ( ) 4 2 3 S x y z dS + + ,(S ) 为平面 1 2 3 4 x y z + + = ,( x y z 0, 0, 0)

4、设F=0,-x,2),S是锥面:=√R2+少上满足0≤x≤1且0≤y≤1部分的下侧。 RUES
4 4、 设 2 F y x z = − ( , , ) , S 是锥面 2 2 z x y = + 上满足 0 1 x 且 0 1 y 部分的下侧。 求 (S) F dS

5、计算r-,其中(心是由点4-1,0)经点B1,0)到点C(-1,2)的路径,AB 4x2+y2 为下半圆周,BC是直线。 5
5 5、 计算 ( ) 2 2 4 L xdy ydx x y − + ,其中 (L) 是由点 A( 1,0) − 经点 B(1,0) 到点 C( 1,2) − 的路径, AB 为下半圆周, BC 是直线

6、将f)=x-lx∈0,2]展开为Fourier余弦级数,并求常数项级数之号的和。 6
6 6、 将 f x x x ( ) 1, [0,2] = − 展开为 Fourier 余弦级数,并求常数项级数 2 1 1 n n + = 的和

7、利用二元Taylor展开式证明当充分小时,cosx≈1-(x-y) cosy 7
7 7、 利用二元 Taylor 展开式证明当 x y , 充分小时, cos 1 2 2 1 ( ) cos 2 x x y y − −

8、求方程(1-x)y”+y=0在0点附近的两个线性无关的幂级数解(写出相应的递 推公式以及每个解的前五项),并给出级数收敛范围。 8
8 8、 求方程 (1 ) 0 − + = x y y 在 0 点附近的两个线性无关的幂级数解(写出相应的递 推公式以及每个解的前五项),并给出级数收敛范围

g、考虑物理中一类重要的数学模型Sine=-Gordo方,程产-产+s血u=0,计算 ax2 812 其形如u=()的解,其中5=x-c1+,c,均为常数。 9
9 9、 考虑物理中一类重要的数学模型 Sine-Gordon 方程: 2 2 2 2 sin 0 u u u x t − + = ,计算 其形如 u = ( ) 的解,其中 0 = − + x ct , 0 c, 均为常数

10、设在不均匀的各向同性的介质中,光的传播速率为(x,y,)= 5习其 中c为真空中的光速,μ为折光率,记集合H为联接点Axo,0)和点B(x,y,)之 间的所有光滑曲线r:=)的集合,利用变分法证明光从4,,)到点 =(x) B(x,片,)的传播路线所满足的微分方程为 V+P+业-44y y+y2+五 =0 √+y+业de 应+y+ =0 yx0)=0,(x)=0 y(x)=,z(x)= 10
10 10、 设在不均匀的各向同性的介质中,光的传播速率为 ( , , ) ( , , ) c v x y z x y z = ,其 中 c 为真空中的光速, 为折光率,记集合 H 为联接点 0 0 0 A x y z ( , , ) 和点 1 1 1 B x y z ( , , ) 之 间的所有光滑曲线 ( ) ( ) y y x z z x = = : 的集合,利用变分法证明光从 0 0 0 A x y z ( , , ) 到点 1 1 1 B x y z ( , , ) 的传播路线所满足的微分方程为 2 2 2 2 2 2 2 2 0 0 0 0 1 1 1 1 1 0 1 1 0 1 ( ) , ( ) ( ) , ( ) d y y z y dx y z d z y z z dx y z y x y z x z y x y z x z + + − = + + + + − = + + = = = =