
第十章 统计回归模型 10.1牙膏的销售量 10.2软件开发人员的薪金 10.3 酶促反应 10.4投资额与国民生产总值和 物价指数 数学建摸
第十章 统计回归模型 10.1 牙膏的销售量 10.2 软件开发人员的薪金 10.3 酶促反应 10.4 投资额与国民生产总值和 物价指数

数学建摸的基本方法 机理分析 测试分析 由于客观事物内部规律的复杂及人们认识程度的限制, 无法分析实际对象内在的因果关系,建立合乎机理规 律的数学模型。 通过对数据的统计分析,找出与数据拟合最好的模型 回归模型是用统计分析方法建立的最常用的一类模型 ·不涉及回归分析的数学原理和方法 通过实例讨论如何选择不同类型的模型 对软件得到的结果进行分析,对模型进行改进 数学建模
回归模型是用统计分析方法建立的最常用的一类模型 数学建模的基本方法 机理分析 测试分析 通过对数据的统计分析,找出与数据拟合最好的模型 • 不涉及回归分析的数学原理和方法 • 通过实例讨论如何选择不同类型的模型 • 对软件得到的结果进行分析,对模型进行改进 由于客观事物内部规律的复杂及人们认识程度的限制, 无法分析实际对象内在的因果关系,建立合乎机理规 律的数学模型
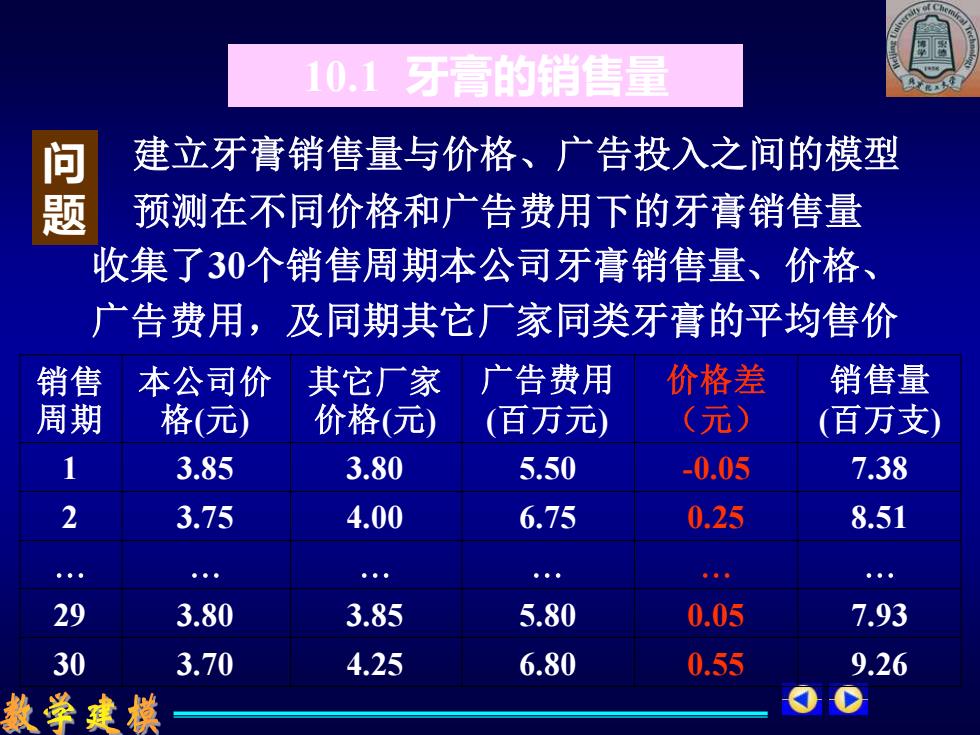
10.1牙膏的销售量 问 建立牙膏销售量与价格、广告投入之间的模型 预测在不同价格和广告费用下的牙膏销售量 收集了30个销售周期本公司牙膏销售量、价格、 广告费用,及同期其它厂家同类牙膏的平均售价 销售 本公司价 其它厂家 广告费用 价格差 销售量 周期 格(元) 价格(元) (百万元) (元) (百万支) 1 3.85 3.80 5.50 -0.05 7.38 2 3.75 4.00 6.75 0.25 8.51 0·。 。。 ”。· ……… 29 3.80 3.85 5.80 0.05 7.93 30 3.70 4.25 6.80 0.55 9.26 数学建摸
10.1 牙膏的销售量 问 题 建立牙膏销售量与价格、广告投入之间的模型 预测在不同价格和广告费用下的牙膏销售量 收集了30个销售周期本公司牙膏销售量、价格、 广告费用,及同期其它厂家同类牙膏的平均售价 30 3.70 4.25 6.80 0.55 9.26 29 3.80 3.85 5.80 0.05 7.93 2 3.75 4.00 6.75 0.25 8.51 1 3.85 3.80 5.50 -0.05 7.38 销售量 (百万支) 价格差 (元) 广告费用 (百万元) 其它厂家 价格(元) 本公司价 格(元) 销售 周期
基本模型 10 9.5 y~公司牙膏销售量 9 0 00 00 0 x一其它厂家与本公司价格差 8.5 08 x2公司广告费用 7.5 0.2 0 0.2 0.4 0.6 y=B。+阝x1+阝2x2+B3x2+8 三所tBx+ y被解释变量(因变量) 10 9.5 6 x1,x2~解释变量(回归变量,自变量) 9 8.5 0 0 B,B1,B,B回归系数 00 0 0 7.5 0 8随机误差(均值为零的 5 5.5 6 6.5 7.5 正态分布随机变量) =+所
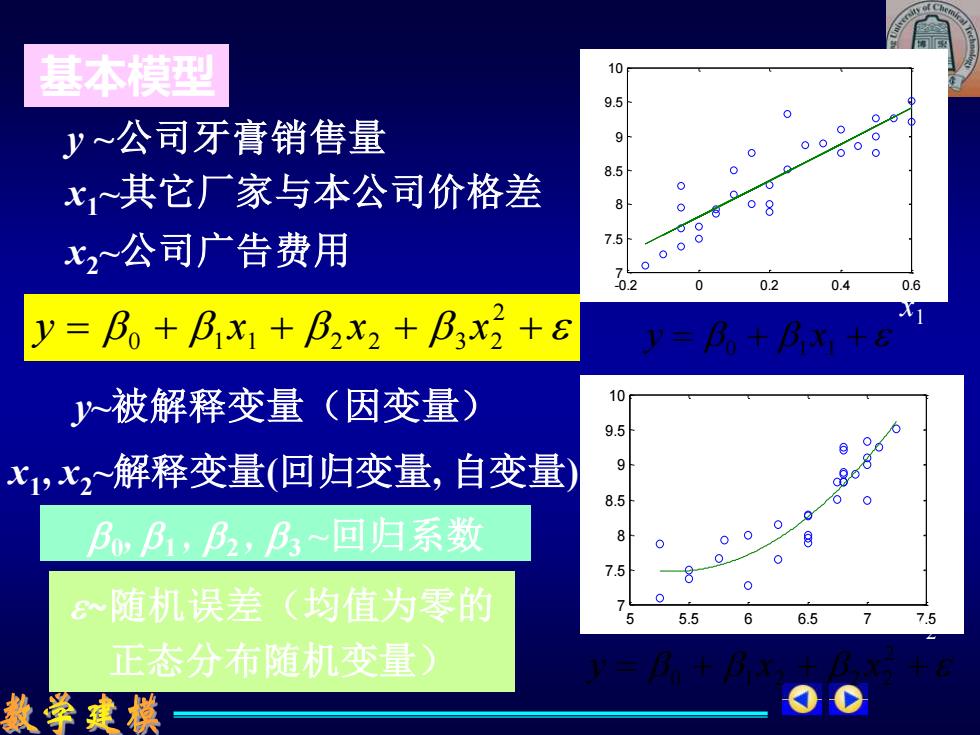
基本模型 y ~公司牙膏销售量 x1 ~其它厂家与本公司价格差 x2 ~公司广告费用 = + + 0 1 1 y x = + + + 2 0 1 2 2 2 y x x 5 5.5 6 6.5 7 7.5 7 7.5 8 8.5 9 9.5 10 x2 y -0.2 0 0.2 0.4 0.6 7 7.5 8 8.5 9 9.5 10 x1 y = + + + + 2 0 1 1 2 2 3 2 y x x x x1 , x2 ~解释变量(回归变量, 自变量) y~被解释变量(因变量) 0 , 1 , 2 , 3 ~回归系数 ~随机误差(均值为零的 正态分布随机变量)
模型求解 MATLAB统计工具箱 B+,+2++6由数据,x1x2估计B [b,bint,r,rint,stats]=regress(y,x,alpha) 输入 y~n维数据向量 输出 b~的估计值 X= [1x,] ~×4数 bint~b的置信区间 据矩阵,第1列为全1向量 x残差向量y-x西 a1pha(置信水平,0.05) rint~r的置信区闻 参数 参数估计值 置信区间 B 17.3244 5.728228.9206 Stats~ 1.3070 I0.6829 1.93111 检验统计量 B2 -3.6956 L-7.49890.10771 R2,F,P F 0.3486 0.03790.65941 数学建 3=0.9054 F=82.9409 p=0.0000
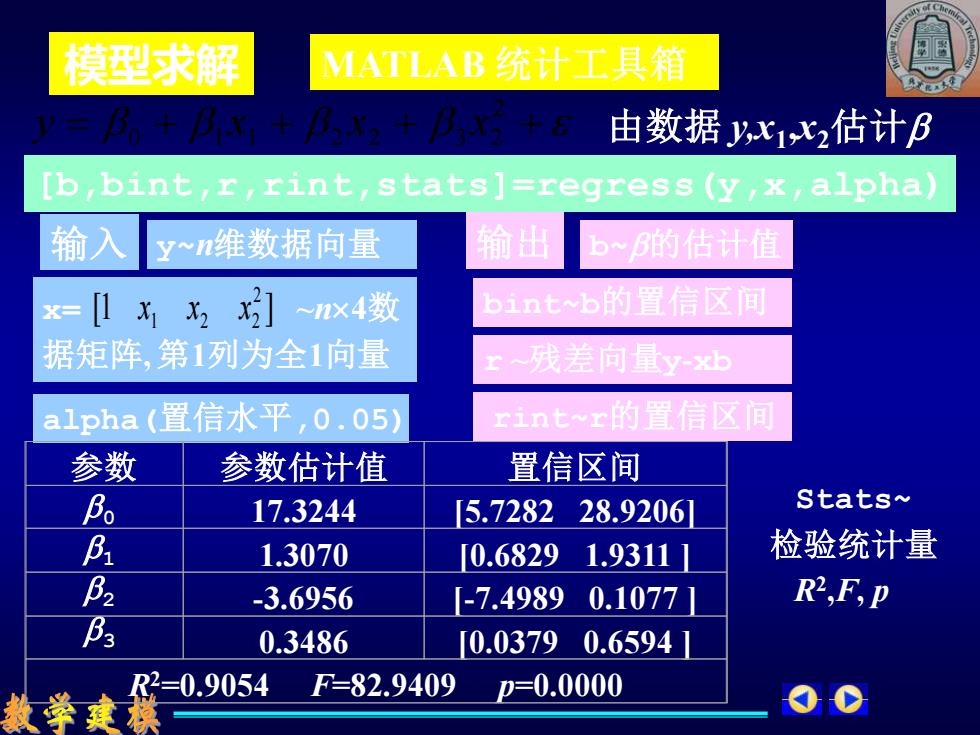
模型求解 MATLAB 统计工具箱 [b,bint,r,rint,stats]=regress(y,x,alpha) 输入 x= ~n4数 据矩阵, 第1列为全1向量 [1 ] 2 1 2 2 x x x alpha(置信水平,0.05) = + + + + 2 0 1 1 2 2 3 2 y x x x b~的估计值 bint~b的置信区间 r ~残差向量y-xb rint~r的置信区间 Stats~ 检验统计量 R2 ,F, p y~n维数据向量 输出 由数据 y,x1 ,x2估计 参数 参数估计值 置信区间 17.3244 [5.7282 28.9206] 1.3070 [0.6829 1.9311 ] -3.6956 [-7.4989 0.1077 ] 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 0 1 2 3

结果分析 参数 参数估计值 置信区间 B。 17.3244 |5.728228.9206 B 1.3070 [0.68291.93111 B2 -3.6956 -7.4989 0.1077] F 0.3486 0.0379 0.65941 R2=0.9054 F=82.9409 p=0.0000 的90.549%可由模型确定 F远超过检验的临界值 匹小于o=0.05 模型从整体上看成立 B,的置信区间包含零点 x,对因变量的 右端点距零点很近 影响不太显著 x,2项显著 可将x,保留在模型中 教学建摸 00
结果分析 y的90.54%可由模型确定 参数 参数估计值 置信区间 17.3244 [5.7282 28.9206] 1.3070 [0.6829 1.9311 ] -3.6956 [-7.4989 0.1077 ] 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 0 1 2 3 = + + + + 2 0 1 1 2 2 3 2 y x x x F远超过F检验的临界值 p远小于=0.05 2的置信区间包含零点 (右端点距零点很近) x2对因变量y 的 影响不太显著 x2 2项显著 可将x2保留在模型中 模型从整体上看成立

1 销售量预测 且,中中名+0 价格差x,=其它厂家价格x本公司价格x 调整x 空制 围过,锁训 控制价格差x,=0.2元,投入广告费x,=650万元 )=B,+Bx+Bx+月x污=8.2933 百万支) 销售量预测区间为7.8230,8.7636](置信度95%) 上限用作库存管理的目标值下限用来把握公司的现金流 若估计x3=3.9,设定x4=3.7,,则可以95%的把握 知道销售额在7.8320x3.7≈29(百万元)以上 数学建摸
2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ 销售量预测 y ˆ = + x + x + x 价格差x1 =其它厂家价格x3 -本公司价格x4 估计x3 调整x4 控制价格差x1 =0.2元,投入广告费x2 =650万元 销售量预测区间为 [7.8230,8.7636](置信度95%) 上限用作库存管理的目标值 下限用来把握公司的现金流 若估计x3 =3.9,设定x4 =3.7,则可以95%的把握 知道销售额在 7.83203.7 29(百万元)以上 控制x1 通过x1 , x2预测y 8.2933 ˆ ˆ ˆ ˆ ˆ 2 y = 0 + 1 x1 + 2 x2 + 3 x2 = (百万支)
模型改进 y= P。+Bx1+B2x2+Bx3 +8 和x,对 参数 参数估计值 置信区间 的影响独立 17.3244 [5.728228.92061 B 1.3070 0.6829 1.9311 B2 -3.6956 -7.4989 0.10771 x,和x对 0.3486 0.03790.65941 的影响有 R2=0.9054 F=82.9409 p=0.0000 交互作用 y=B+Bx+B2x2+B:x2+Bax x2+ 参数 参数估计值 置信区间 29.1133 [13.701344.5252 B 11.1342 1.977820.29061 -7.6080 L-12.6932-2.52281 0.6712 I0.25381.08871 B -1,4777 -2.8518-0.10371 R2=0.9209 F=72.7771 教学建模 p0.06
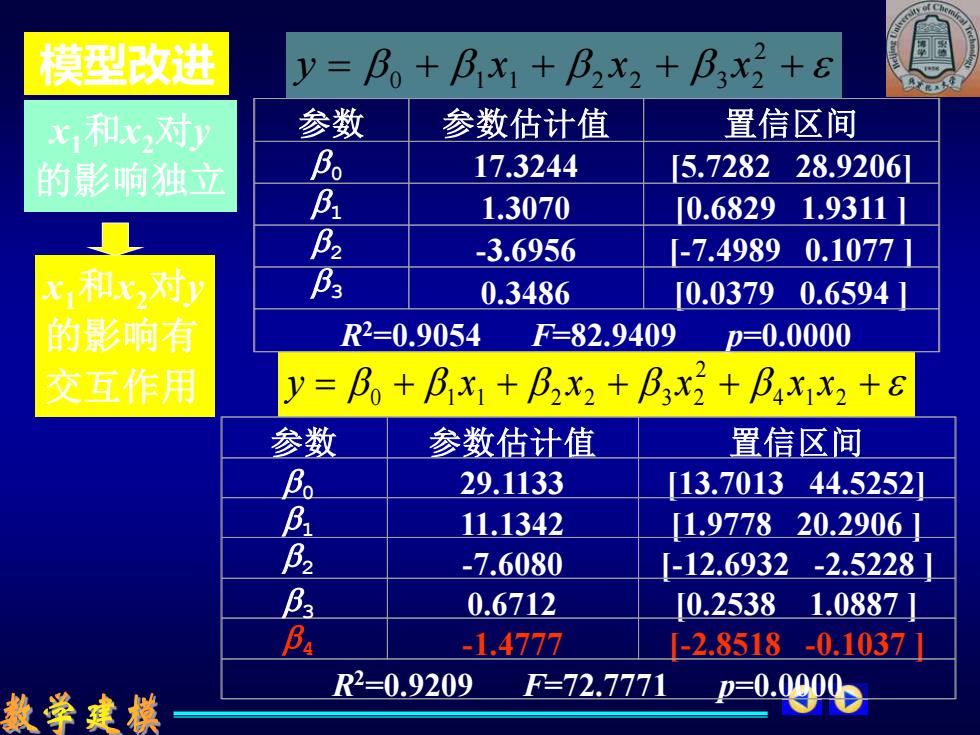
模型改进 x1和x2对y 的影响独立 = + + + + 2 0 1 1 2 2 3 2 y x x x = + + + + + 4 1 2 2 0 1 1 2 2 3 2 y x x x x x 参数 参数估计值 置信区间 17.3244 [5.7282 28.9206] 1.3070 [0.6829 1.9311 ] -3.6956 [-7.4989 0.1077 ] 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 0 1 2 3 参数 参数估计值 置信区间 29.1133 [13.7013 44.5252] 11.1342 [1.9778 20.2906 ] -7.6080 [-12.6932 -2.5228 ] 0.6712 [0.2538 1.0887 ] -1.4777 [-2.8518 -0.1037 ] R2=0.9209 F=72.7771 p=0.0000 3 0 1 2 4 x1和x2对y 的影响有 交互作用

两模型销售量预测比较 控制价格差x,=0.2元,投入广告费x2=6.5百万元 )= 8.2933 百万支 )=月。+Bx+Bx2+Bx号 ☒间7.8230,8.7636 )=8.3272(百万支 =B+Bx+B2x2+阝x3+Bxx2 间17.8953,8.7592 略有增加 预测区间长度更短 数学建摸
两模型销售量预测比较 4 1 2 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x + x x 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x y ˆ = 8.2933 (百万支) 区间 [7.8230,8.7636] 区间 [7.8953,8.7592] y ˆ = 8.3272 (百万支) 控制价格差x1 =0.2元,投入广告费x2 =6.5百万元 y ˆ 略有增加 预测区间长度更短

两模型少与心,关系的比较 了=中有t+xs+民中+B 9 9 8.5 8.5 x=6.5 8 8 7.5 0.2 7.5 0.2 0.4 0.6 .2 0 0.2 0.40.6 o 10.5 9.5 10 x1=0.2 9.5 8.5 9 8 8.5 7.5 8 6 个 2 5 6 8
x2 =6.5 x1 =0.2 -0.2 0 0.2 0.4 0.6 7.5 8 8.5 9 x1 y ˆ -0.2 0 0.2 0.4 0.6 7.5 8 8.5 9 x1 y ˆ 5 6 7 8 7.5 8 8.5 9 9.5 10 x2 y ˆ 5 6 7 8 8 8.5 9 9.5 10 10.5 x2 y ˆ 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x 4 1 2 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x + x x 两模型 与x1 y ˆ ,x2关系的比较