
优化模型 存储模型 森林救火 奶制品的生产与销售 接力队的选拔与选课策略 实例:投资的效益和风险 MATLAB优化工具箱 BUCT
BUCT

3.1 存贮模型 问题 配件厂为装配线生产若干种产品,轮换产品时因更换设 备要付生产准备费,产量大于需求时要付贮存费。该厂 生产能力非常大,即所需数量可在很短时间内产出。 已知某产品日需求量100件,生产准备费5000元,贮存费 每日每件1元。试安排该产品的生产计划,即多少天生产 一次(生产周期),每次产量多少,使总费用最小。 要不只是回答问题,而且要建立生产周期、产量与 求需求量、准备费、贮存费之间的关系。 BUCT
BUCT 3.1 存贮模型 问 题 配件厂为装配线生产若干种产品,轮换产品时因更换设 备要付生产准备费,产量大于需求时要付贮存费。该厂 生产能力非常大,即所需数量可在很短时间内产出。 已知某产品日需求量100件,生产准备费5000元,贮存费 每日每件1元。试安排该产品的生产计划,即多少天生产 一次(生产周期),每次产量多少,使总费用最小。 要 求 不只是回答问题,而且要建立生产周期、产量与 需求量、准备费、贮存费之间的关系

问题分析与思考 日需求100件,准备费5000元,贮存费每日每件1元。 每天生产一次,每次100件,无贮存费,准备费5000元。 每天费用5000元 10天生产一次,每次1000件,贮存费900+800+..+100=4500 元,准备费5000元,总计9500元。 平均每天费用950元 50天生产一次,每次5000件,贮存费4900+4800+…+100 =122500元,准备费5000元,总计127500元。 平均每天费用2550元 10天生产一次平均每天费用最小吗? BUCT
BUCT 问题分析与思考 • 每天生产一次,每次100件,无贮存费,准备费5000元。 日需求100件,准备费5000元,贮存费每日每件1元。 • 10天生产一次,每次1000件,贮存费900+800+…+100 =4500 元,准备费5000元,总计9500元。 • 50天生产一次,每次5000件,贮存费4900+4800+…+100 =122500元,准备费5000元,总计127500元。 平均每天费用950元 平均每天费用2550元 10天生产一次平均每天费用最小吗? 每天费用5000元

问题分析与思考 ·周期短,产量小 贮存费少,准备费多 ·周期长,产量大 准备费少,贮存费多 存在最佳的周期和产量,使总费用(二者之和)最小 这是一个优化问题,关键在建立目标函数 显然不能用一个周期的总费用作为目标函数 目标函数 每天总费用的平均值 BUCT
BUCT 这是一个优化问题,关键在建立目标函数 显然不能用一个周期的总费用作为目标函数 目标函数——每天总费用的平均值 • 周期短,产量小 • 周期长,产量大 问题分析与思考 贮存费少,准备费多 准备费少,贮存费多 存在最佳的周期和产量,使总费用(二者之和)最小

模型假设 1.产品每天的需求量为常数r; 2.每次生产准备费为c1,每天每件产品贮存费为c2 3.T天生产一次(周期),每次生产Q件,当贮存量 为零时,Q件产品立即到来(生产时间不计); 4.为方便起见,时间和产量都作为连续量处理。 建棋目的 设5c,c2已知,求T,Q使每天总费用的平均值最小。 BUCT
BUCT 模 型 假 设 1. 产品每天的需求量为常数 r; 2. 每次生产准备费为 c1 , 每天每件产品贮存费为 c2; 3. T天生产一次(周期), 每次生产Q件,当贮存量 为零时,Q件产品立即到来(生产时间不计); 建 模 目 的 设 r, c1 , c2已知,求T, Q 使每天总费用的平均值最小。 4. 为方便起见,时间和产量都作为连续量处理
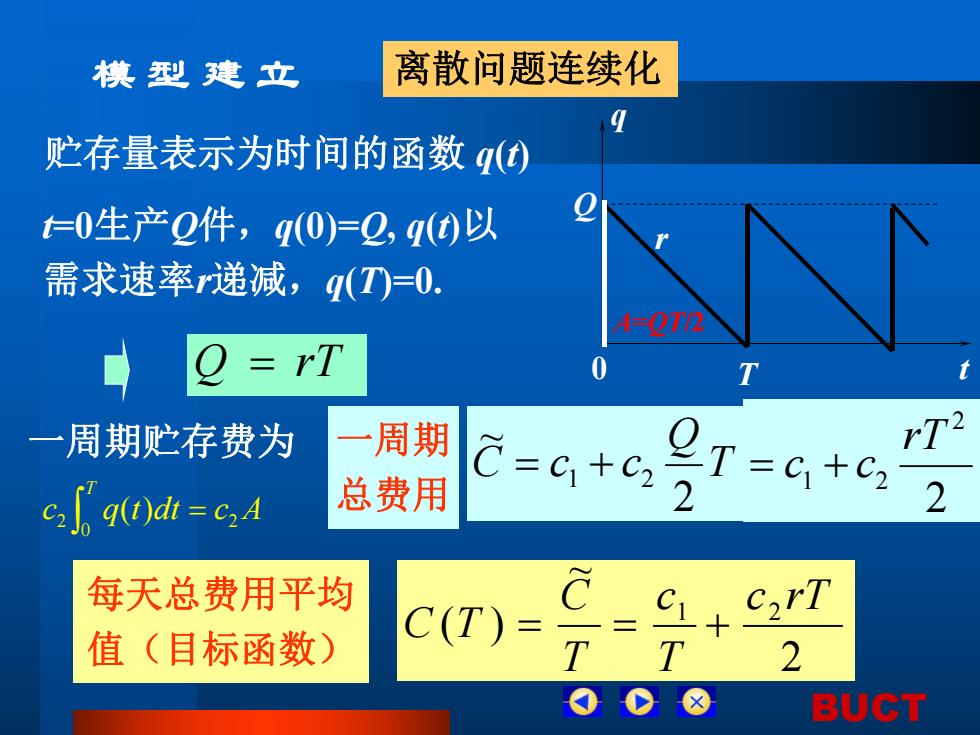
模型建立 离散问题连续化 贮存量表示为时间的函数q) 0生产0件,q(0)=2,q0以 需求速率递减,q(T=0. rT 一周期贮存费为 周期 C=c+c2 rT2 99)d=c5A 总费用 2 2 每天总费用平均 a 值(目标函数) C(T)= T T 2 8 BUCT
BUCT 模 型 建 立 0 t q 贮存量表示为时间的函数 q(t) T Q r t=0生产Q件,q(0)=Q, q(t)以 需求速率r递减,q(T)=0. 一周期 总费用 T Q C c c 2 ~ 1 2 每天总费用平均 值(目标函数) 2 ~ ( ) 1 2 c rT T c T C C T 离散问题连续化 c q t dt c A T 2 0 2 ( ) 一周期贮存费为 A=QT/2 2 2 1 2 rT c c Q rT

型求解 求T使C(T)= T= 2C1 dT Q=rT= 2cr rC 2 C2 棋型分析 g↑→I,Q个 9↑→T,Q↓ r个-T,Q个 携型应用 c1=5000,c2=1,=100 ·回答问题 T=10(天),2=1000(件),C=1000(元) BUCT
BUCT 模型求解 Min 2 ( ) 1 2 c rT T c 求 T 使C T 0 dT dC 2 2 1 c c r Q rT 2 2 1 rc c T 模型分析 c1T,Q c2 T,Q r T ,Q 模型应用 c1=5000, c2=1,r=100 • 回答问题 T=10(天), Q=1000(件), C=1000(元)

经济批量订货公式(EOQ公式) 用于订货、供应、存贮情形 每天需求量r,每次订货费c,每天每件贮存费c2, T天订货一次(周期),每次订货Q件,当贮存量降到 零时,Q件立即到货。 T Q=rT= 2cr rC 2 C2 不允许缺货的存贮模型 ·问:为什么不考虑生产费用?在什么条件下才不考虑? BUCT
BUCT • 经济批量订货公式(EOQ公式) 2 2 1 rc c T 2 2 1 c c r Q rT 每天需求量 r,每次订货费 c1 ,每天每件贮存费 c2, 用于订货、供应、存贮情形 不允许缺货的存贮模型 • 问:为什么不考虑生产费用?在什么条件下才不考虑? T天订货一次(周期), 每次订货Q件,当贮存量降到 零时,Q件立即到货

允许缺货的存贮模型 当贮存量降到零时仍有需求, 出现缺货,造成损失 原模型假设:贮存量降到零时Q件 立即生产出来(或立即到货) 现假设:允许缺货,每天每件缺货损失费3,缺货需补足 周期T,T贮存量降到零 一周期 一周期总费用 贮存费 c.q(t)di=c,A 一周期 缺货费 cq(t)di=c,B 2 BUCT
BUCT 允许缺货的存贮模型 A 0 B q Q r T1 t 当贮存量降到零时仍有需求r, 出现缺货,造成损失 原模型假设:贮存量降到零时Q件 立即生产出来(或立即到货) 现假设:允许缺货, 每天每件缺货损失费 c3 , 缺货需补足 T 1 Q rT c q t dt c A T 2 0 2 1 ( ) 一周期 贮存费 c q t dt c B T 3 T 3 1 一周期 ( ) 缺货费 周期T, t=T1贮存量降到零 2 ( ) 2 2 1 3 1 1 2 r T T c QT C c c 一周期总费用

周期总费用 =c+,c+,cT-T) 每天总费用 平均值 TT 2rT 2rT (目标函数) 求T,2使 C(T,Q)→Min ac ac 为与不允许缺货的存贮模型 相比,T记作T',Q记作2 T 2c1C2+C3 2cr C3 rC2 C3 C2 C2+C3 BUCT
BUCT rT c rT Q rT c Q T c T C C T Q 2 ( ) 2 ( , ) 2 3 2 1 2 0 , 0 Q C T C 每天总费用 平均值 (目标函数) 2 1 2 1 3 1 ( ) 2 1 2 1 一周期总费用 C c c QT c r T T 求 T ,Q 使 C (T , Q ) Min 3 2 3 2 2 1 c c c rc c T 2 3 3 2 2 1 c c c c c r Q 为与不允许缺货的存贮模型 相比,T记作T ’ , Q记作Q’