
第四节】 ezier曲面 教学建模 00
第四节 Bézier曲面

一.Bezier曲面的定义 定义6.4.1设P,=01,n,j=0,1m为n+)×(m+1) 个空间点列,则m×n次张量积形式的Bezier 曲面定义为: P,)=22P月,a)B) uvE i=0j=0 其中Bnu=Cm-wB.=Cy0-v) 是Bernstein基函数。依次用线段连接点 P,射0,1,…,mj=01,…,m)中相邻两点所形成的 空间网格,称之为特征网格。Bezier曲面的 矩阵表示式是: 数学建模
一. Bézier曲面的定义 定义6.4.1 设 P (i n j m) ij = 0,1, , = 0,1, 为 (n +1)(m +1) 个空间点列,则 mn 次张量积形式的Bézier 曲面定义为: ( , ) ( ) ( ) , 0,1 0 0 = , , = = P u v P B u B v u v m i n j i j i m j n 其中 ( ) ( ) i i m i i m m B u C u u − , = 1− ( ) ( ) j j n j j n m B v C v v − , = 1− 是Bernstein基函数。依次用线段连接点 P ( 列 i m j n) ij = 0,1, , ; = 0,1, , 中相邻两点所形成的 空间网格,称之为特征网格。Bézier曲面的 矩阵表示式是:

Bo.m B Pu,y)=[Bn(a,B(a),…,Bn(u】 Po .m P nm n.m 二.Bezier曲面的性质 Bezier曲面特征网格的四个角点正好是Bezier 曲面的四个角点,即 P0,0)=P。P1,0=P。 P0,1=P. P0,1)=Pm 2.Bezier曲面特征网格最外一圈顶点定义Bezier 曲面的四条边界;Bezierl曲面边界的跨界切矢只 与定义该边界的顶点及相邻一排顶点有关,且 数学建模
( ) ( ) ( ) ( ) = m m m m n n n m m m n n n n B B B P P P P P P P P P P u v B u B u B u , 1, 0, 0 1 1 0 1 1 1 0 0 0 1 0 0, 1, , , , , , 二. Bézier , 曲面的性质 Bézier曲面特征网格的四个角点正好是Bézier 曲面的四个角点,即 ( ) 0 00 P 0, = P ( ) 0 0 1, P = P m ( ) P 1 P0n 0, = ( ) P = P mn 1, 1 2. Bézier曲面特征网格最外一圈顶点定义Bézier 曲面的四条边界;Bézier曲面边界的跨界切矢只 与定义该边界的顶点及相邻一排顶点有关,且
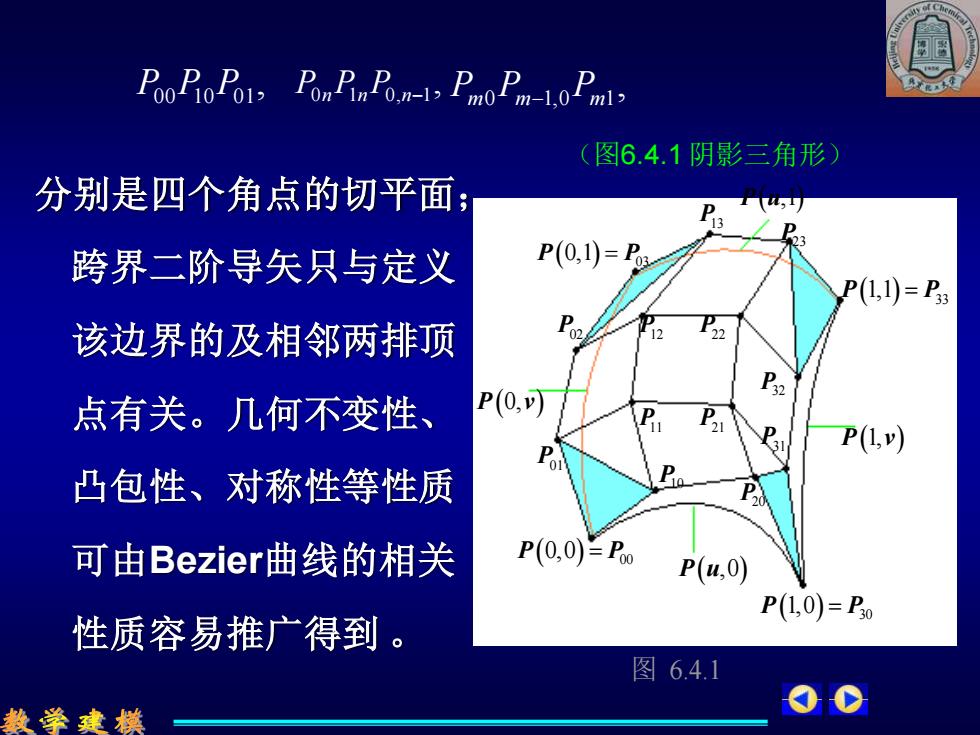
Poo Pon n Fom-1 Pmo P D m-1,02ml (图6.4.1阴影三角形) 分别是四个角点的切平面; 跨界二阶导矢只与定义 P(0,1)=P P(1,=P 该边界的及相邻两排顶 点有关。几何不变性、 P(0, P(1,) 凸包性、对称性等性质 D 可由Bezierl曲线的相关 P(0,0)=Po P(u,0) P(1,0)=P0 性质容易推广得到。 图6.4.1 数学建模
, P00P10P01 , P0n P1n P0,n−1 , Pm0 Pm−1,0 Pm1 (图6.4.1 阴影三角形) 分别是四个角点的切平面; 跨界二阶导矢只与定义 该边界的及相邻两排顶 点有关。几何不变性、 凸包性、对称性等性质 可由Bezier曲线的相关 性质容易推广得到 。 ( ) 00 P P 0,0 = ( ) 30 P P 1,0 = ( ) 03 P P 0,1 = ( ) 33 P P 1,1 = P01P02 P11 P12P10 P13 P20 P21 P22 P23 P31 P32 P v (0, ) P v (1, ) P u( ,0) P u( ,1) 图 6.4.1

三.BezierE曲面片的拼接 如图6.4.2所示,设两张m×n次Bezierl曲面片 21,1) Pa,-∑ΣPBaB. P(1,1)=2(0, 0a,)=Σ∑2,B.u)B.(付 2(u,) P(O.1YP(u.v) 21,0) u,ve0,1] 1,0)=2(0,0) P(C0) 分别由控制顶点,Q,定义。 图6.4.2 如果要求两曲面片达到G连续, 则它们有公共的边界,即: 教学建模
三. Bézier曲面片的拼接 如图6.4.2所示,设两张m×n次Bézier曲面片 ( ) ( ) ( ) ( ) ( ) ( ) , 0, 1 , , 0 0 , , 0 0 , , = = = = = = u v Q u v Q B u B v P u v P B u B v m i n j ij i m j n m i n j ij i m j n P(0,1) P(0,0) Q(1,0) Q(1,1) P Q (1,1 0,1 ) = ( ) P Q (1,0 0,0 ) = ( ) P u v ( , ) Q u v ( , ) v u 图6.4.2 分别由控制顶点 , Pij Qij 定义。 如果要求两曲面片达到 0 G 连续, 则它们有公共的边界,即:

P(1,v)=Q0,) (6.4.1) 于是有 Pa =C0r (i=0,1,…,m) 如果又要求沿该公共边界达到G连续,则两曲 面片在该边界上有公共的切平面,因此曲面的 法向应当是跨界连续的,即: 2.0,v)x2,(0,v)=c)P.L)×P1,v) (6.4.2)》 下面来研究满足这个方程的两种方法。 a.鉴于(6.4.1),(6.4.2)式最简单的解是: 20,v=a()PL,v) (6.4.3) 数学建模
P (1, v) = Q (0, v) (6.4.1) 于是有 P Q (i m ) ni i , 0, 1, , = 0 = 如果又要求沿该公共边界达到 1 G 连续,则两曲 面片在该边界上有公共的切平面,因此曲面的 法向应当是跨界连续的,即: Q ( v) Q ( v) (v)P ( v) P ( v) u v u v 0, 0, = 1, 1, (6.4.2) 下面来研究满足这个方程的两种方法。 a. 鉴于(6.4.1),(6.4.2)式最简单的解是: Q ( v) (v)P ( v) u u 0, = 1, (6.4.3)

这相当于要求合成曲面上y为常数的所有曲线,在 跨界时有切向的连续性。为了保证等式两边关于y 的多项式次数相同,必须取a)=α(一个正常数) 于是有:QQ=PP- (a>0,i=0,l,…,m 即2-Qo=aPnm-Pn)(a>0,i=01,…m) b.(6.4.3)式使得两张曲面片在边界达到G连续 时,只涉及曲面Pu,y)和Q4,)的两列控制顶点 用这种方法匹配合成的曲面的边界,向和向是 光滑连续的。以: Q.(0,v)=av)P1,)+B)P,) (6.4.4) 来满足(6.4.2)式,这仅仅要求Q,0,v)位于 教学建模
这相当于要求合成曲面上 为常数的所有曲线,在 跨界时有切向的连续性。为了保证等式两边关于 的多项式次数相同,必须取 (v) = (一个正常数) 于是有: Q Q P P ( i m) i i ni n i 0, 0,1, , 1 0 = −1, = 即 Q Q (P P ) ( i m) 1i − 0i = n i − n−1,i 0, = 0,1, b.(6.4.3)式使得两张曲面片在边界达到 1 G 连续 时,只涉及曲面 P(u,v) 和 Q(u,v) 的两列控制顶点 用这种方法匹配合成的曲面的边界, 向和 向是 光滑连续的。以: Q ( v) (v)P ( v) (v)P ( v) u u v 0, = 1, + 1, (6.4.4) 来满足(6.4.2)式,这仅仅要求 Q ( v) u 0, 位于 v v u v

P,),P,)所在的同一个平面内,也就是 曲面片Pu,)边界上相应点处的切平面,这 样就有了大得多的余地,但跨界切矢在跨越 曲面片的边界时就不再连续了。为了保证 等式两边关于V的多项式次数相同,心) 是的任意线性函数。&须为任意正常数, 数学建模
P (1,v), u P ( v) v 1, 所在的同一个平面内,也就是 曲面片 P(u,v) 边界上相应点处的切平面,这 样就有了大得多的余地,但跨界切矢在跨越 曲面片的边界时就不再连续了。为了保证 项式次数相同, 须为任意正常数, (v) 是 的任意线性函数。 v v 等式两边关于 的多