
20 概率论与数理统计问题 的计算机求解 教学建模
1 概率论与数理统计问题 的计算机求解

主要内容 慨率分布与伪随机数生成 统计量分析 数理统计分析方法及计算机实现 统计假设检验 方差分析及计算机求解 教学建模
2 • 概率分布与伪随机数生成 • 统计量分析 • 数理统计分析方法及计算机实现 • 统计假设检验 • 方差分析及计算机求解 主要内容

9.1 概率分布与伪随机数生成 。1 概率密度函数与分布函数概述 常见分布的概率密度函数与分布函 数 概率问题的求解 随机数与伪随机数 数学建模
3 9.1 概率分布与伪随机数生成 • 概率密度函数与分布函数概述 • 常见分布的概率密度函数与分布函 数 • 概率问题的求解 • 随机数与伪随机数

9,1,1概率密度数与分布函数概述 连续随机变量概率密度记为p(x) 概率密度函数满足: p(x)≥0,且 p(xdx=1 概率分布函数: r-Cpu 教学建摸
4 9.1.1 概率密度函数与分布函数概述

20 概率分布函数F(x)的物理意义: 随机变量ξ满足ξ≤x发生的概率 函数为单调递增函数,并且满足: 0≤F(x)≤1,且F(-o)=0,F(o)=1 数学建摸
5

9.1.2常见分布的概率密度 函数与分布函数 9.1.2.1 Poisson:布 Poisson分布的概率密度为: Pp(x) ex=0.1,23 其中λ为正整数 教学建模 6
6 9.1.2 常见分布的概率密度 函数与分布函数 9.1.2.1 Poisson分布
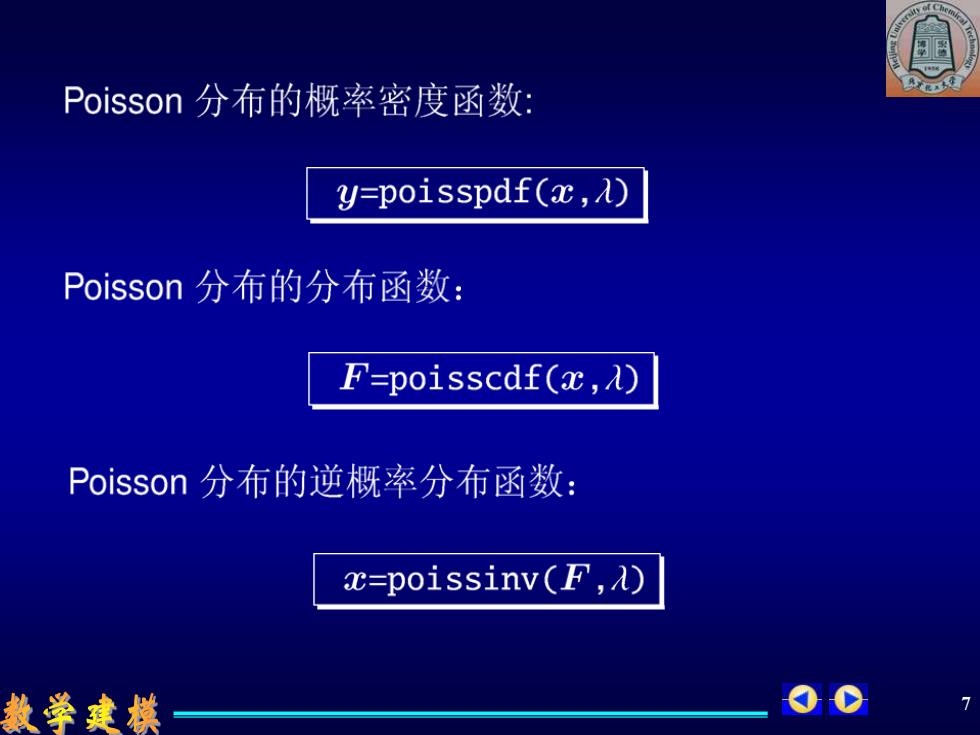
20 Poisson分布的概率密度函数: y=poisspdf(c,λ) Poisson分布的分布函数: F=poisscdf(x,λ) Poisson分布的逆概率分布函数: c=poissinv(F,λ) 数学建模 00
7
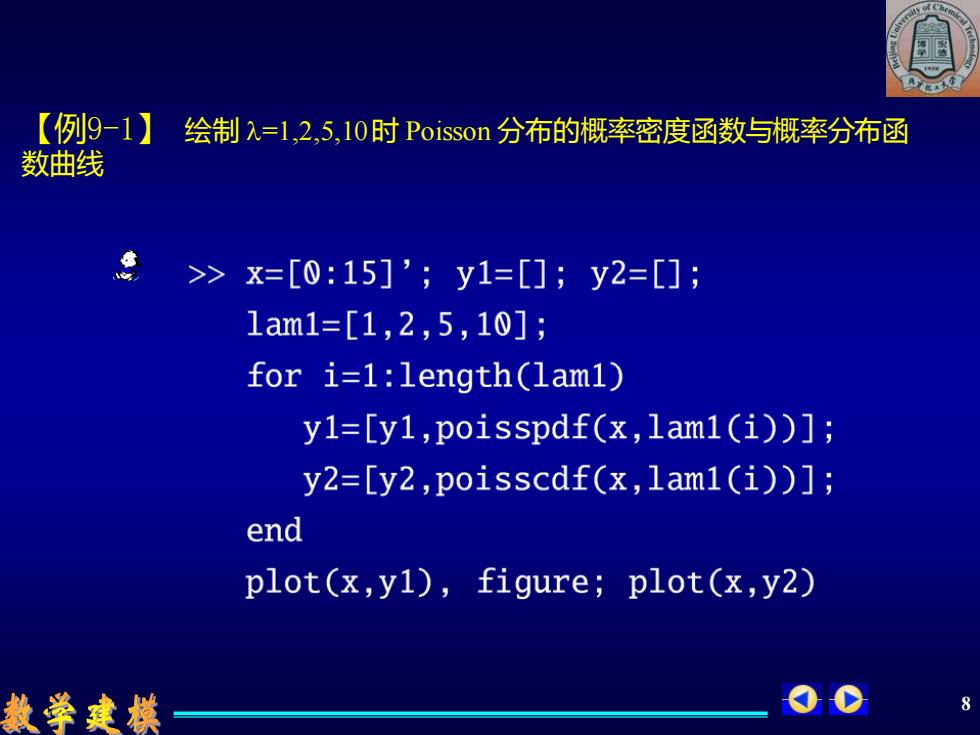
【例9-1】 绘制入=1,2,5,10时Poisson分布的概率密度函数与概率分布函 数曲线 >x=[0:15]';y1=[];y2=[]; 1am1=[1,2,5,10]; for i=1:length(lam1) y1=[y1,poisspdf(x,lam1(i))]; y2=[y2,poisscdf(x,lam1(i))]; end plot(x,y1),figure;plot(x,y2) 教学建模 8
8 【例9-1】 绘制 l=1,2,5,10 时 Poisson 分布的概率密度函数与概率分布函 数曲线

9.1.2.2正态分布 正态分布的概率密度函数为: -x-)2 Pn(x) e 2o2 其中1和σ2分别为正态分布的均值和方差 数学建摸
9 9.1.2.2 正态分布 正态分布的概率密度函数为:

y=normpdf(x,u,o) F=normcdf(x,u,o) c=norminv(F,u,c) 教学建摸 10
10