
第十一章 马氏链模型 11.1健康与疾病 11.2钢琴销售的存贮策略 11.3基因遗传 11.4等级结构 数学建摸
第十一章 马氏链模型 11.1 健康与疾病 11.2 钢琴销售的存贮策略 11.3 基因遗传 11.4 等级结构

马氏链模型 描述一类重要的随机动态系统(过程)的模型 ·系统在每个时期所处的状态是随机的 ·从一时期到下时期的状态按一定概率转移 ·下时期状态只取决于本时期状态和转移概率 已知现在,将来与过去无关(无后效性) 马氏链(Markov Chain) 时间、状态均为离散的随机转移过程 教学建模
马氏链模型 • 系统在每个时期所处的状态是随机的 • 从一时期到下时期的状态按一定概率转移 • 下时期状态只取决于本时期状态和转移概率 已知现在,将来与过去无关(无后效性) 描述一类重要的随机动态系统(过程)的模型 马氏链 (Markov Chain) ——时间、状态均为离散的随机转移过程

11.1健康与疾病 通过有实际背景的例子介绍马氏链的基本概念和性质 人的健康状态随着时间的推移会随机地发生转变 保险公司要对投保人未来的健康状态作出估计,以制 订保险金和理赔金的数额 例1.人的健康状祝分为健康和疾病两种状态,设对特 定年龄段的人,今年健康、明年保特健康状态的概率 为0.8,而今年患病、明年转为健康状态的概率为0.7, 若某人投保时健康,问10年后他仍处于健康状态的概率 数学建模
通过有实际背景的例子介绍马氏链的基本概念和性质 例1. 人的健康状况分为健康和疾病两种状态,设对特 定年龄段的人,今年健康、明年保持健康状态的概率 为0.8, 而今年患病、明年转为健康状态的概率为0.7, 11.1 健康与疾病 人的健康状态随着时间的推移会随机地发生转变 保险公司要对投保人未来的健康状态作出估计, 以制 订保险金和理赔金的数额 若某人投保时健康, 问10年后他仍处于健康状态的概率
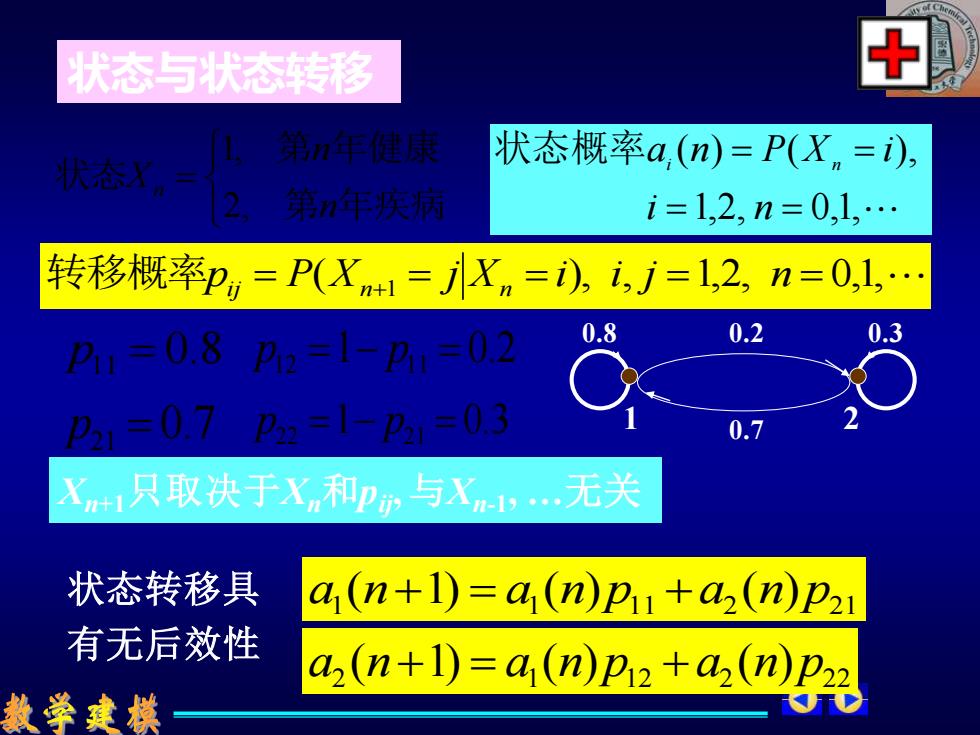
状态与状态转移 第年健成 状态概率a,(n)=P(Xn=i), 第年疾肩 i=1,2,n=0,1,… 转移概率p=P(X1=Xn=),i,j=1,2,n=0,1… 月,=08P2=1-A,=02 0.8 0.2 0.3 2,=072=1-,=03 0.7 X+1只取决于Xw和P,与Xn,无关 状态转移具 a,(n+1)=a,(n)p1+a2(n)p2 有无后效性 a2(n+1)=a(n)p2+a2(n)p22 教学建摸
转移概率pi j = P(Xn+1 = j Xn = i), i, j =1,2, n = 0,1, Xn+1只取决于Xn和pij, 与Xn-1 , …无关 p11 = 0.8 1 0.2 p12 = − p11 = 0.7 p21 = 1 0.3 p22 = − p21 = = 第 年疾病 第 年健康 状态 n n Xn 2, 1, 1,2, 0,1, ( ) ( ), = = = = i n a n P X i 状态概率 i n 状态与状态转移 状态转移具 有无后效性 1 1 11 2 21 a (n+1) = a (n)p +a (n)p 1 2 0.8 0.2 0.3 0.7 2 1 12 2 22 a (n+1) = a (n)p + a (n)p

状态与状态转移 0.8 0.2 0.3 a,(n+1)=a,(n)p1+a2(n)p2i 给定(O),预测 a2(n+1)=a,(n)p2+a2(n)p22 a(n),n=1,2.. n 0 2 00 设投保 a1(n) 1 0.8 0.78 0.778 7/9 时健康 a2(n) 0 0.2 0.22 0.222 2/9 设投保 a (n 0 0.7 0.77 0.777 7/9 时疾病 4(n) 0.3 0.33 0.333.. 2/9 →时状态概率趋于稳定值,稳定值与初始状态无关 款学建模
n 0 a2 (n) 0 a1 设投保 (n) 1 时健康 给定a(0), 预测 a(n), n=1,2… 设投保 时疾病 a2 (n) 1 a1 (n) 0 n→时状态概率趋于稳定值,稳定值与初始状态无关 + = + + = + 2 1 1 2 2 2 2 1 1 1 1 2 2 1 ( 1) ( ) ( ) ( 1) ( ) ( ) a n a n p a n p a n a n p a n p 3 … 0.778 … 0.222 … ∞ 7/9 2/9 0.7 0.77 0.777 … 0.3 0.33 0.333 … 7/9 2/9 状态与状态转移 1 2 0.8 0.2 0.3 0.7 1 0.8 0.2 2 0.78 0.22
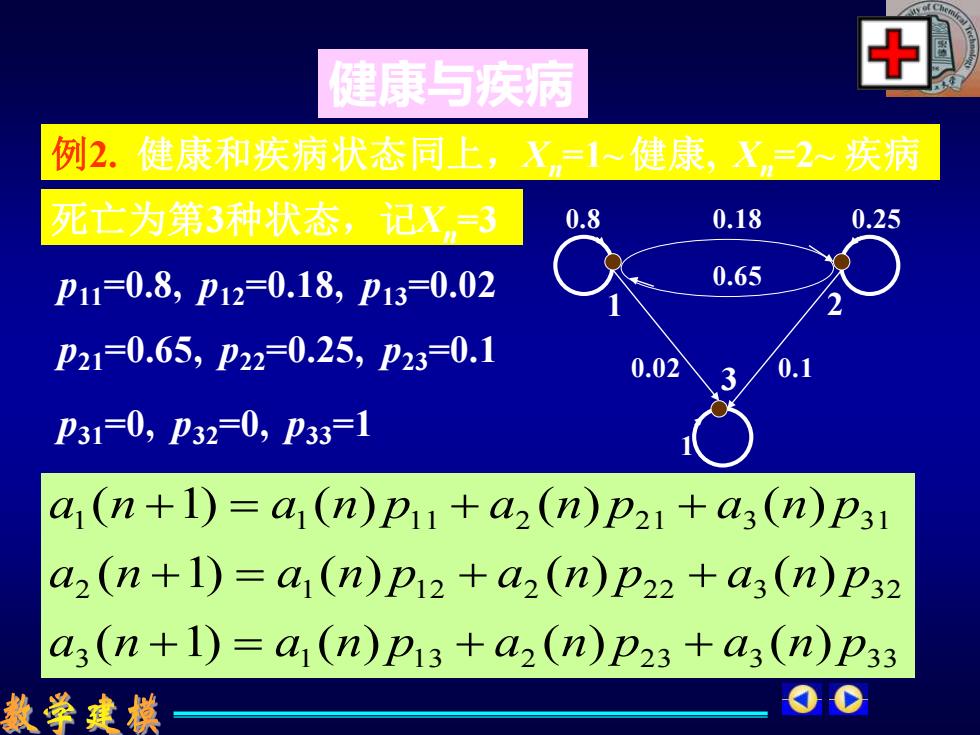
健康与疾病 例2.健康和疾病状态同上,X=1~健康,X=2疾病 死亡为第3种状态,记X=3 0.8 0.18 0.25 p11=0.8,p12=0.18,p13=0.02 0.65 P21=0.65,p22=0.25,p23=0.1 0.02 P31=0,p32=0,P33=1 a1(n+1)=a(n)p11+a2(n)p21+a3(n)p31 a2(n+1)=a,(n)p12+a2(n)p22+a3(n)p32 a3(n+1)=a1(n)p13+a2(n)p23+a3(n)p33 教学建摸
1 2 3 0.02 0.1 1 0.8 0.18 0.25 0.65 例2. 健康和疾病状态同上,Xn=1~ 健康, Xn=2~ 疾病 3 1 1 3 2 2 3 3 3 3 2 1 1 2 2 2 2 3 3 2 1 1 1 1 2 2 1 3 3 1 ( 1) ( ) ( ) ( ) ( 1) ( ) ( ) ( ) ( 1) ( ) ( ) ( ) a n a n p a n p a n p a n a n p a n p a n p a n a n p a n p a n p + = + + + = + + + = + + p11=0.8, p12=0.18, p13=0.02 死亡为第3种状态,记Xn=3 健康与疾病 p21=0.65, p22=0.25, p23=0.1 p31=0, p32=0, p33=1

状态与状态转移 中 设投保时处于健康状态,预测a(n),n=1,2. n 0 2 3 50 0 a(n) 1 0.8 0.7570.7285 0.1293 。。 0 42(n 0 0.180.189 0.1835.. 0.0326. 0 a;(n 0 0.020.0540.0880.. 0.8381. 不论初始状态如何,最终都要转到状态3; ·一旦a1k)=2)=0,3(k)=1,则对于>k,a1n=0, a2()=0,3(n=1,即从状态3不会转移到其它状态。 数学建模
n 0 1 2 3 a2 (n) 0 0.18 0.189 0.1835 a3 (n) 0 0.02 0.054 0.0880 a1 (n) 1 0.8 0.757 0.7285 设投保时处于健康状态,预测 a(n), n=1,2… • 不论初始状态如何,最终都要转到状态3 ; • 一旦a1 (k)= a2 (k)=0, a3 (k)=1, 则对于n>k, a1 (n)=0, a2 (n)=0, a3 (n)=1, 即从状态3不会转移到其它状态。 状态与状态转移 0 0 1 50 0.1293 0.0326 0.8381

马氏链的基本方程 伏存1=12,川=国 状态概字和=P(.Y,三) 7=12,k,1=0 转移概率p,=P(X1=jX,=) p,20,∑P,=li=12,…k 基本方程 a,(n+1)=∑a,(0p,i=1,2,…,k 1)=(a107).,a( a(n+1)=a(n)P 状态概率向冒 P=P,转移率矩陶 a(n)=a(0)P" 非负.行为 教学建模
1,2,, , 0,1, ( ) ( ), = = = = i k n a n P X i 状态概率 i n ( ) 1 p P X j X i 转移概率 ij = n+ = n = X =1,2, k (n = 0,1, ) 马氏链的基本方程 状态 n ( ) 1 1 = = a n k i i p p i k k j i j i j 0, 1, 1,2, , 1 = = = (非负,行和为 ) 转移概率矩阵 1 P ={pi j}kk ~ a(n +1) = a(n)P a n a n p i k k j i j j i ( 1) ( ) , 1,2, , 1 + = = = 基本方程 ~ 状态概率向量 ( ) ( ( ), ( ), , ( )) 1 2 a n a n a n a n = k n a(n) = a(0)P

马氏链的两个重要类型 a7+三m 1.正则链~从任一状态出发经有限次转移 能以正概率到达另外任一状态(如例1) E则链今3V,P'>0 正则链→3N,a(n)一→代n-→oo)w~稳态概率 w满足wP=W 08w,+0711 0.802 0024=0.7w 0.703 021,十031三1 w满足 w,=1 1m=7/92/9 i=l 数学纸保】
w满足 wP = w 马氏链的两个重要类型 1. 正则链 ~ 从任一状态出发经有限次转移 能以正概率到达另外任一状态(如例1)。 , 0 N 正则链 N P a(n +1) = a(n)P 正则链w, a(n) →w(n →) = 0.7 0.3 0.8 0.2 例1. P w = (7 / 9,2 / 9) 1 2 2 1 2 1 0.2 0.3 0.8 0.7 w w w w w w + = + = 1 1 = = k i w满足 wi 1 w1 +w2 = 1 2 0.2w = 0.7w w ~ 稳态概率

马氏链的两个重要类型 2 吸收链~存在吸收状态 (一旦到达就不会离 开的状态,P一),且从任一非吸收状态出发经有 限次转移能以正概率到达吸收状态(如例2) 有个吸收状态的吸收链 R有非 的转移概率阵标准形式 零元素 M=(1-)'=∑Q y=()=6 y~从第i个非吸收状态出发,被某个 吸收状态吸收前的平均转移次数。 教学建摸
= R Q I P r r 0 马氏链的两个重要类型 2. 吸收链 ~ 存在吸收状态(一旦到达就不会离 开的状态i, pii=1),且从任一非吸收状态出发经有 限次转移能以正概率到达吸收状态(如例2)。 有r个吸收状态的吸收链 的转移概率阵标准形式 R有非 零元素 = − = − = 0 1 ( ) s s M I Q Q T e = (1,1, ,1) y y y y Me = ( 1 , 2 , k−r ) = yi ~ 从第 i 个非吸收状态出发,被某个 吸收状态吸收前的平均转移次数