参4社会经济统的中量过程 例能源利用朱统的预测 一能源利用量; V2 V4 2—能源价格; 3一能源生产率; V4一—环境质量; V5一工业产值; V6一就业机会; V5+ V6 V7一人口总数。 带待号的有向图
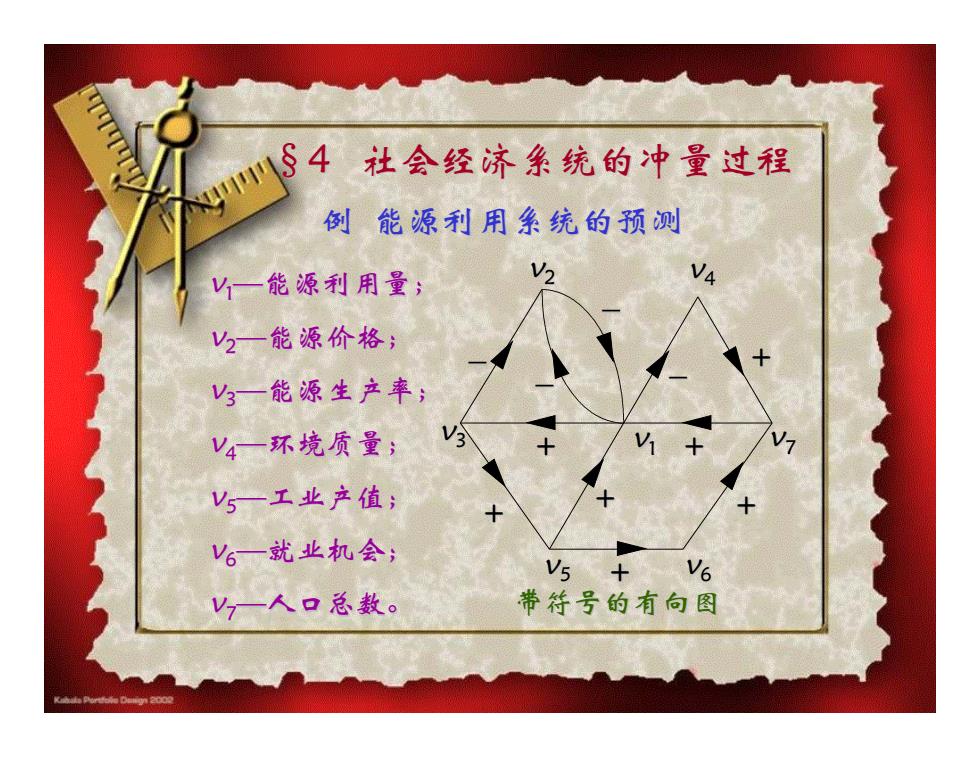
v1 — 能源利用量; v2 — 能源价格; v3 — 能源生产率; v4 — 环境质量; v5 — 工业产值; v6 — 就业机会; v7 — 人口总数。 带符号的有向图 例 能源利用系统的预测 v7 v2 v4 v3 v1 v5 v6 – – – – + + + + + + + §4 社会经济系统的冲量过程

系统的元素 图的顶点 元素间的影响■ 带方向的孤 影响的正反面 孤旁的十、一号 影响—直接影响 待号一容观规律;方针政策
系统的元素— — 图的顶点 元素间的影响— — 带方向的弧 影响的正反面— — 弧旁的+、– 号 影响— — 直接影响 符号— — 客观规律;方针政策

带符号有向图C1=(V,的邻接矩阵A V人项点集E~孤集 定性模型 若yy,为 + a 若vy,为 0, 若yy,EE 0 -11 -1000 00 0000 0 -10 0100 带特号的有向图G1 A 0 00 0001 1 0 0 0010 ++y 0 00 000 某时段V增加导致下 0 0 000 0 时段V增加减少
ï î ï í ì Ï - - + = v v E v v v v a i j i j i j ij , 若 若 为 , 若 为 0 1, 1 ú ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ê ë é - - - - = 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 A 带符号有向图G1=(V,E)的邻接矩阵A V~顶点集 E~弧集 定性模型 v - i vj + 某时段vi 增加导致下 时段vj 增加减少 带符号的有向图G1 v7 v2 v4 v3 v1 v5 v6 – – – – + + + + + + +

加权有向图G2及其邻接矩阵W 0.3 某时段y增加1单位导致下时 0.8 段V增加W单位 -0.508 -1.200 0 加权有向图G2 01 0 0 000 0 00 -2 0 01 0 定量模型 0 0 0000.3 205 0 0 001.5 0 0 0 000 1 0 0 0 0 0 0 A视为W的特例
ú ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ê ë é - - - - = 1.5 0 0 0 0 0 0 0 0 0 0 0 0 1 1.2 0 0 0 0 1.5 0 0 0 0 0 0 0 0.3 0 2 0 0 1 0 0 0.7 0 0 0 0 0 0 0 0.5 0.8 1.2 0 0 0 W 加权有向图G2及其邻接矩阵W 定量模型 某时段vi 增加1单位导致下时 段vj 增加wij单位 j w i v v ¾¾®ij A视为 W的特例 加权有向图G2 v3 v2 v4 v7 v1 v5 v6 -2 -0.5 -0.7 -1.2 0.3 1 1.5 0.8 1.5 1 1.2

冲量过程(Pulse Process) y→y 研究由某元素V:变化引起的系统的演变过程 V()一V在时段t的值; P(因~V在时段t的改变量(冲量) y(t+l)=y,(t)+p.(t+1),i=1,2,…,nt=0,1,2, p,(t+1)=∑w,P,(t),或p,t+1)=∑aP,() i=l
vi (t +1) = vi (t) + pi (t +1), i =1,2,L,n, t = 0,1,2,L å å = = + = + = n i n i j ij i j ij i p t w p t p t a p t 1 1 ( 1) ( ), 或 ( 1) ( ) 冲量过程(Pulse Process) 研究由某元素vi变化引起的系统的演变过程 vi (t) ~ vi在时段t 的值; pi (t) ~ vi在时段t 的改变量(冲量) j w i v v ¾¾®ij

vt)=(4(0y(t)2,y(t) pO=(p(t),P(),…pn() 冲量过程模型 v(t+1)=v(t)+p(t+1) p(t+1)=p(t)W 或 p(1+1)=p(1)A
v(t +1) = v(t) + p(t +1) ( ) ( ( ), ( ), , ( )) ( ) ( ( ), ( ), , ( )) 1 2 1 2 p t p t p t p t v t v t v t v t n n L L = = 冲量过程模型 p(t + 1) = p(t)W p (t + 1) = p (t) A 或

能源利用系统的预测 v(t+1)=v(t)+p(t+1) p(t+1)=p(1)A 设v(0)=p(0) 简单冲量过程—— 初始冲量p(O)中 某个分量为1,其余为0的冲量过程 若开始时能源利用量有突然增加, 预测条统的演变 能源利用系统的p()和V(t)
能源利用系统的预测 简单冲量过程— — 初始冲量p(0)中 某个分量为1,其余为0的冲量过程 若开始时能源利用量有突然增加, 预测系统的演变 v(0) = p(0) v(t + 1) = v(t) + p(t + 1) p(t + 1) = p(t) A 设 能源利用系统的 p(t)和v(t)

t P.P.Ps P。p y,3 VV 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 -1 0 0 1 0 .1 2 .2 -1 3 -11-1010 332 -2
2 3 1 -1 0 0 1 0 -1 2 -2 1 -1 1 0 -1 1 -1 1 -1 0 1 0 3 -3 2 -2 1 1 -1 LL LL 1 0 -1 1 -1 0 0 0 1 -1 1 -1 0 0 0 t 2 p3 p4 p5 p6 p7 p 4 v 3 v 2 v 1 v 5 v 6 v 7 v 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 p1

简单冲量过程S的稳定性 ·任意时段S的各元素的值和冲量是否为有限(稳定) ·S不稳定时如何改变可以控制的关华使之变为稳定 p(t+1)=p(t)Wv(t+1)=v(t)+p(t+1) S冲量稳定~对任意i,t,P()|有界 值稳定 S值稳定~对任意i,t,|y()」有界 冲量稳定 P(U)=P(0)WS的稳定性取决于W的特征根 记W的非零特征根为入
简单冲量过程S的稳定性 •任意时段S的各元素的值和冲量是否为有限(稳定) •S不稳定时如何改变可以控制的关系使之变为稳定 S冲量稳定~对任意 i,t, | pi (t) |有界 S值稳定~对任意 i,t, | vi (t) |有界 值稳定 冲量稳定 W v(t + 1) = v(t) + p(t + 1) p (t + 1) = p (t ) t p(t) = p(0)W S的稳定性取决于W的特征根 记W的非零特征根为l

心简草冲量过程S的稳定性 S冲量稳定→|2|≤1 ·|2|≤1且均为单根→S冲量稳定 ·S值稳定台S冲量稳定且不等于1 对于能源利用集统的邻接矩阵A 「0-11-1000 -1000000 特征多项式 0-100100 f(0)=22(0-入-2-1) A= 04000001 1000010 0 000001 000000 f①=-2,f2)=76032(1,2) 能源利用系统存在冲量不稳定的简单冲量过程
•S冲量稳定 Þ |l | £ 1 •|l | £ 1且均为单根 Þ S冲量稳定 •S值稳定 Û S冲量稳定且l不等于1 ú ú ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ê ê ë é - - - - = 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 A 对于能源利用系统的邻接矩阵A ( ) ( 1) 2 5 3 2 f l = l l - l - l - 特征多项式 f (1) = -2, f (2) = 76 $lÎ(1,2) 能源利用系统存在冲量不稳定的简单冲量过程 简单冲量过程S的稳定性