
第一章 绪论与初等数学模型
第一章 绪论与初等 数学模型

第一节现实与模型 内容: §1.1 原型和模型 §1.2 数学模型 §1.3 数学模型的意义 §1.4现实对象与数学模型的关华
第一节 现实与模型 内容: §1.1 原型和模型 §1.2 数学模型 §1.3 数学模型的意义 §1.4 现实对象与数学模型的关系

§1.1原型和模型 回原型是指人们在现实世界里关心、研 究或者从事生产、管理的实际对象 口模型则指为了某个特定目的将原型的某 部分信息简缩、提炼而构造的原型的模拟物 模型不是原型的简单复制,原型有各个方面 和各种层次。一个原型,为了不同目的可以 有许多不同的模型作为它的模拟物,这些模 型分别从不同侧面模拟该原型
q 原型是指人们在现实世界里关心、研 究或者从事生产、管理的实际对象 q 模型则指为了某个特定目的将原型的某一 部分信息简缩、提炼而构造的原型的模拟物 模型不是原型的简单复制,原型有各个方面 和各种层次。一个原型,为了不同目的可以 有许多不同的模型作为它的模拟物,这些模 型分别从不同侧面模拟该原型。 §1.1 原型和模型

§1.2数学模型 航行问题 甲乙两地相距750公里,船从甲地到乙 地顺水航行需30小时,从乙地到甲地逆水 需50小时,问船速、水速各若干? 这是一个经过简化且非常理想化的实际问题 解这个代数应用题的过程体 现了数学模型的基本内容
航行问题 这是一个经过简化且非常理想化的实际问题 解这个代数应用题的过程体 现了数学模型的基本内容 甲乙两地相距750公里,船从甲地到乙 地顺水航行需30小时,从乙地到甲地逆水 需50小时,问船速、水速各若干? §1.2 数学模型

解: ①设船速为X公里/小时, 水速为y公里/小时 根据建立数学模型的目地和问题的背景 作必要的简化假设,并确定变量与参数 (x+y)30=750 ②依题意: (x-y)50=750 利用相应的物理或其他规律列出数学式子, 列出的二元一次方程组就是一种数学结构, 即为数学模型
根据建立数学模型的目地和问题的背景 作必要的简化假设,并确定变量与参数 解: ①设船速为x公里/小时, 水速为y公里/小时 ②依题意: î í ì - × = + × = ( ) 50 750 ( ) 30 750 x y x y 利用相应的物理或其他规律列出数学式子 , 列出的二元一次方程组就是一种数学结构, 即为数学模型

③求解得 x=20,y=5 模型求解,得出数学上的解答 ④答: 船速为20公里小、时,水速为5公里/小时。 用数学上的解答解释原问题 作为数学模型的全过程, 最后还要用实际现象来验证上述结果
模型求解,得出数学上的解答 ③求解得 x = 20, y = 5 ④答: 船速为20公里/小时,水速为5公里/小时。 用数学上的解答解释原问题 作为数学模型的全过程, 最后还要用实际现象来验证上述结果

我们可以这样定义数学模型: 数学模型是关于部分现实世界和为 种特殊目的而作的一个抽象的、简化 的数学结构 将实际问题抽象成数学问题,这是建立数学 模型的关键一步,取决与建模者对数学知识 的掌握和对问题的透彻分析 将实际问题进行合理的简化是必要的,简化 的过程是找出问题本质的过程,但这往往是 困难的
我们可以这样定义数学模型: q 数学模型是关于部分现实世界和为 一种特殊目的而作的一个抽象的、简化 的数学结构 将实际问题抽象成数学问题,这是建立数学 模型的关键一步,取决与建模者对数学知识 的掌握和对问题的透彻分析 将实际问题进行合理的简化是必要的,简化 的过程是找出问题本质的过程,但这往往是 困难的

§13数学模型的意义 (为什么需要数学模型) 数学的特点不仅在于它的抽象性、严密性和确 定 性 (即定量的描述),而且在于它应用的广泛性。 在上个世纪,数学的应用不仅在传统领域继续取 得许多重要进展,而且迅速进入了非物理领域,如 经济、交通、人口、生态、医学、社会学等领域, 产生了许多边缘学科。特别是电子计算机的迅速发 展,数学己渗透到自然科学、工农业生产、经济活 动与社会生话的各个领域
数学的特点不仅在于它的抽象性、严密性和确 定性(即定量的描述),而且在于它应用的广泛性。 在上个世纪,数学的应用不仅在传统领域继续取 得许多重要进展,而且迅速进入了非物理领域,如 经济、交通、人口、生态、医学、社会学等领域, 产生了许多边缘学科。特别是电子计算机的迅速发 展,数学已渗透到自然科学、工农业生产、经济活 动与社会生活的各个领域。 §1.3 数学模型的意义 (为什么需要数学模型)

般地说,当实际问题需要我们对所研 究的现实对象提供分析、预报、决策、 控制等方向的定量结果时,往往都离不 开数学的应用,而建立数学模型则是这 个过程的关键环节
一般地说,当实际问题需要我们对所研 究的现实对象提供分析、预报、决策、 控制等方向的定量结果时,往往都离不 开数学的应用,而建立数学模型则是这 个过程的关键环节
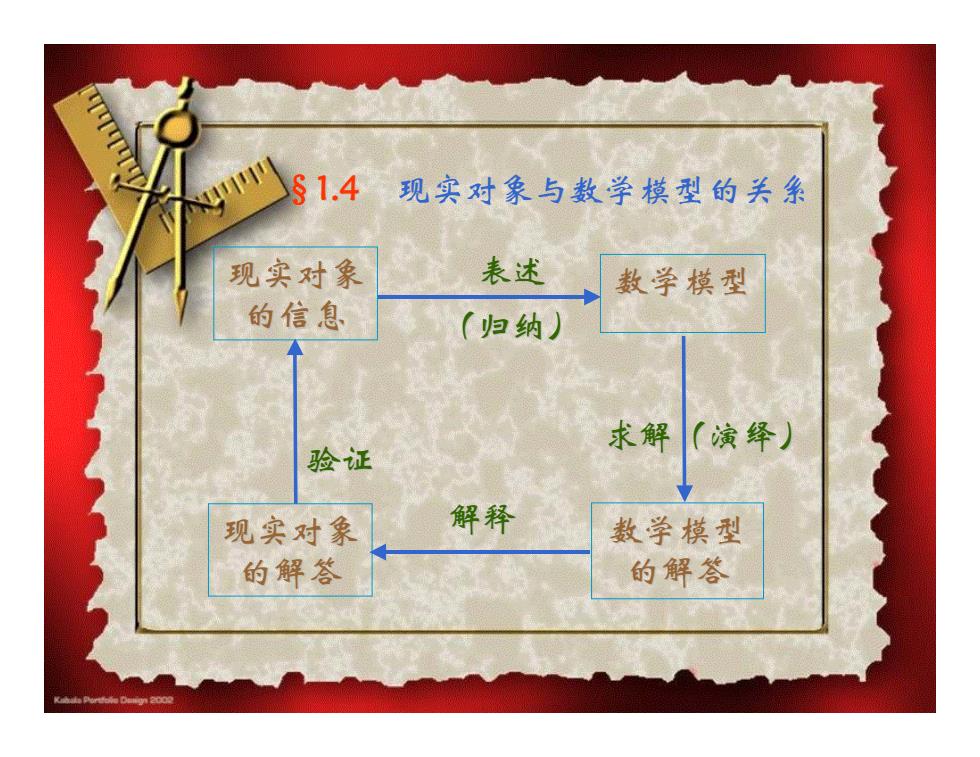
§1.4 现实对象与数学模型的关华 现实对象 表述 数学模型 的信息 (归纳) 求解 (演绎) 验证 现实对象 解释 数学模型 的解答 的解答
§1.4 现实对象与数学模型的关系 现实对象 的信息 数学模型 数学模型 的解答 现实对象 的解答 解释 验证 求解(演绎) (归纳) 表述