
第二节 建立数学模型的方法和步骤 内容 §2.1建立数学模型的方法 §2.2建摸的步骤
第二节 建立数学模型的方法和步骤 内容: §2.1 建立数学模型的方法 §2.2 建模的步骤

§2.1 建立数学模型的方法 机理分析:根据对现实对象特性的 认识,分析因果关系,找出反映内部机理的规 律。建立的模型常有明确的物理或现实意义。 2、测试分析:将研究对象视为一个“黑箱”系 统,内部机理无法直接寻求,可以测量系统的 输入输出数据,运用统计分析方法,按照事先 确定的准则,在某一类模型中选出一个数据拟 合得最好的模型,这种方法称为系统辨识
1. 机理分析:根据对现实对象特性的 认识,分析因果关系,找出反映内部机理的规 律。建立的模型常有明确的物理或现实意义。 2. 测试分析:将研究对象视为一个“黑箱”系 统,内部机理无法直接寻求,可以测量系统的 输入输出数据,运用统计分析方法,按照事先 确定的准则,在某一类模型中选出一个数据拟 合得最好的模型,这种方法称为系统辨识。 §2.1 建立数学模型的方法

3、 将以上两种方法结合起来也是 常用的建模方法,即用机理分析建立 模型的结构,用系统辨识确定模型的参数
3. 将以上两种方法结合起来也是 常用的建模方法,即用机理分析建立 模型的结构,用系统辨识确定模型的参数
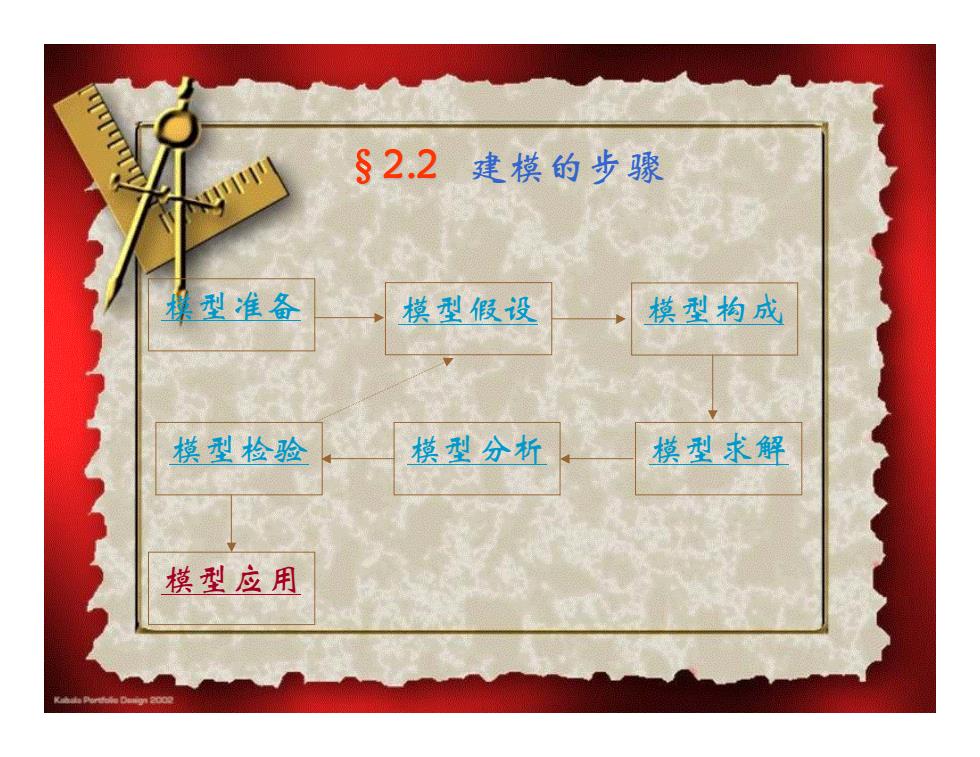
§2.2建模的步骤 提型准备 模型假设 模型构成 模型检验 模型分析 模型求解 模型应用
模型检验 模型分析 模型求解 模型准备 模型假设 模型构成 模型应用 §2.2 建模的步骤

模型的准备现实问题往往是复杂 而零乱的,所以有必要认真审题。弄 清什么是要求的,什么是己知的,是确定 型的还是随机型的问题等等。了解问题的 实际背景,明确建模的目的后,搜集必须 的各种信息,如现象、数据等
q 模型的准备 现实问题往往是复杂 而零乱的,所以有必要认真审题。弄 清什么是要求的,什么是已知的,是确定 型的还是随机型的问题等等。了解问题的 实际背景,明确建模的目的后,搜集必须 的各种信息,如现象、数据等

模型假设根据对象的特征和建模 的目的,对问题进行抽象和必要、合 理的简化,用精确的语言作出假设。作 假设的依据,一是出于对问题内在规律的认 识,二是来自对数据或现象的分析,也可以 是二者的综合。作假设时要运用与问题相关 的知识,又要充分发挥想象力、洞察力和判 断力,善于辨别问题的主次,抓住主要因素, 尽量将问题线性化、均匀化
q 模型假设 根据对象的特征和建模 的目的,对问题进行抽象和必要、合 理的简化,用精确的语言作出假设。作 假设的依据,一是出于对问题内在规律的认 识,二是来自对数据或现象的分析,也可以 是二者的综合。作假设时要运用与问题相关 的知识,又要充分发挥想象力、洞察力和判 断力,善于辨别问题的主次,抓住主要因素, 尽量将问题线性化、均匀化

个实际问题不经过简化假设就很 翻译成数学问题,即使可能也会 很难求解,不同的假设会得到不同的模 型 假设过分简单,会导致模型的失败或 部分失败,假设过分详细,将使问题过分 复杂,可能使你很难甚至无法继续下一步 的工作。因而模型的假设不是一蹴而就的, 往往要视模型的求解过程和模型的检验结 果,对假设进行修改
一个实际问题不经过简化假设就很 难翻译成数学问题,即使可能也会 很难求解,不同的假设会得到不同的模 型,假设过分简单,会导致模型的失败或 部分失败,假设过分详细,将使问题过分 复杂,可能使你很难甚至无法继续下一步 的工作。因而模型的假设不是一蹴而就的, 往往要视模型的求解过程和模型的检验结 果,对假设进行修改

模型构成 建立数学模型。根据 所作的假设,利用对象的内在规律 和适当的数学工具,建立各个量(常 量和变量)之间的(等式或不等式)关系 或其他数学结构。 为完成这一步,需要一些相关的专门知识外 还常常需要较广阔的应用数学方面的知识。 建模应遵循的一个原则是,尽量采用简单的 数学工具,因为建立一个模型总希望有更多 人了解和使用
q 模型构成 建立数学模型。根据 所作的假设,利用对象的内在规律 和适当的数学工具,建立各个量(常 量和变量)之间的(等式或不等式)关系 或其他数学结构。 为完成这一步,需要一些相关的专门知识外, 还常常需要较广阔的应用数学方面的知识。 建模应遵循的一个原则是,尽量采用简单的 数学工具,因为建立一个模型总希望有更多 人了解和使用

模型求解选择适当的数学方法求得数 学模型的解。可以用解方程、图形、证 明定理、逻辑运算、数值计算等各种传统 和近代的数学方法,特别是计算机技术。 使用各种数学软件和软件包,已是解决问题 的必不可少的手段
q 模型求解 选择适当的数学方法求得数 学模型的解。可以用解方程、图形、证 明定理、逻辑运算、数值计算等各种传统 和近代的数学方法,特别是计算机技术。 使用各种数学软件和软件包,已是解决问题 的必不可少的手段

模型分析对模型解答进行数学上 的分析,有时要根据问题的性质分析变 量问的依赖关系或稳定状况,有时根据 所得结果给出数学上的预报,有时则可 能要给出数学上的最优决策和控制,还 常常需要进行误差分析,模型对数据的 稳定性、灵敏性分析等
q 模型分析 对模型解答进行数学上 的分析,有时要根据问题的性质分析变 量间的依赖关系或稳定状况,有时根据 所得结果给出数学上的预报,有时则可 能要给出数学上的最优决策和控制,还 常常需要进行误差分析,模型对数据的 稳定性、灵敏性分析等