
第五章 离散模型
第五章 离 散 模 型

内容: §1 消防设施与监狱看守 §2 循环比赛的名次 §3红绿灯的调节 §4社会经济系统的冲量过程 S5锁具装箱问题 §6效益的合理分配
内容: § 1 消防设施与监狱看守 § 2 循环比赛的名次 § 3 红绿灯的调节 § 4 社会经济系统的冲量过程 § 5 锁具装箱问题 § 6 效益的合理分配

§1.消防设施与监狱看守 问题1(消防设施问题): 若干条街道构成居民小区,如图1所 示,( 1,e2,e7表示街道,,2,,5 表示交叉路口。现计划在某些路口安置消防 设施,只有与路口直接相连的街道才能使用 它们。为使所有街道必要时都有消防设施可 用,在那些路口安置设施才最节省呢?
问题1(消防设施问题): 若干条街道构成居民小区,如图1所 示,e1 , e2 … , e7 表示街道, v1 , v2 ,… , v5 表示交叉路口。现计划在某些路口安置消防 设施,只有与路口直接相连的街道才能使用 它们。为使所有街道必要时都有消防设施可 用,在那些路口安置设施才最节省呢? §1. 消防设施与监狱看守
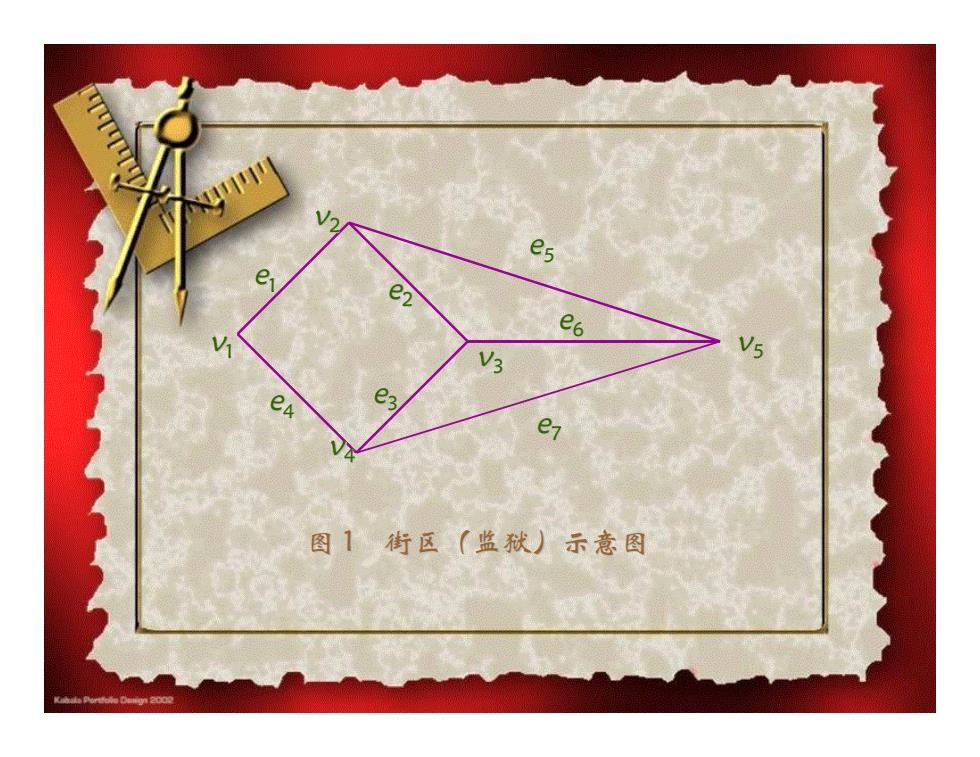
e 图1街区(监狱)示意图
v 1 v 2 v 3 v 4 v 5 e 1 e 2 e 4 e 3 e 5 e 6 e 7 图 1 街区(监狱)示 意 图

问题2(监狱看守问题): 座监狱的几间牢室有道路相连, 妨设其示意图也为图1,M,2,,V5表 示牢室,e1,e2,., e表示道路。监狱看守 要设在通过道路能直接监视所有牢室的地 方,如果看守不得走动,那么他们应呆在 某些牢室(即路口)所在地。问至少需要几 名看守才能完成监视任务呢?
问题2(监狱看守问题): 一座监狱的几间牢室有道路相连, 不妨设其示意图也为图1, v1 , v2 ,… , v5表 示牢室, e1 , e2 ,… , e7表示道路。监狱看守 要设在通过道路能直接监视所有牢室的地 方,如果看守不得走动,那么他们应呆在 某些牢室(即路口)所在地。问至少需要几 名看守才能完成监视任务呢?

上面两个问题的模型已经很自然的地 用图表示出来,也不难用图的性质和算法 解决。 为了叙述的方便,首先简单地介绍 一下图的一些基本概念
上面两个问题的模型已经很自然的地 用图表示出来,也不难用图的性质和算法 解决。 为了叙述的方便,首先简单地介绍 一下图的一些基本概念

图是由项点集V=(y.2,,V 边集E=(e,e2,,em)以及各个项点 和各边之间确定的关联关系平组成的一种 结构,记作图G=(V,E,平),我们常常简 记为G=(V,目。 图还可以用下面两种矩阵表示
图是由顶点集V =(v1 , v2 , … , vn )、 边集E = (e1 , e2 , … , em) 以及各个顶点 和各边之间确定的关联关系Ψ组成的一种 结构,记作图G = (V, E,Ψ ),我们常常简 记为G = (V, E)。 图还可以用下面两种矩阵表示

关联矩阵(Incidence Matrix) (rinxm' n为顶点,数,m为边数 其中 r可 1, 若v,与e关联 0,否则 邻接矩阵(Adjacency Matrix.) A=(aij)nxn' n为顶点数 其中 1,若v与v相邻 0,否则
R=(rij)n×m, n为顶点数,m为边数, 其中 ï î ï í ì = ,否则 , 若 与 关联 0 1 i j ij v e r 邻接矩阵(Adjacency Matrix) A=(aij)nxn, n为顶点数 其中 ï î ï í ì = ,否则 , 若 与 相邻 0 1 i j ij v v a 关联矩阵(Incidence Matrix)

消防设施的安置 在每个路口都安置消防设施显然可 以达到每条街道都可以使用的目的,但 这是不必要的。去掉V5,在,2,3,V4 各安置一个也可达到目的。再去掉V,在V2, V3,V4安置一个仍然可以。此时不能再去掉 了。不难发现,在V,3,V5或2,V4,V5各 安置一个也可以,但是只在2个路口安置消 防设施是不行的,所以最少应该安置3个设 施
在每个路口都安置消防设施显然可 以达到每条街道都可以使用的目的,但 消防设施的安置 这是不必要的。去掉v5 , 在v1 , v2 , v3 , v4 各安置一个也可达到目的。再去掉v1 ,在v2 , v3 , v4安置一个仍然可以。此时不能再去掉 了。不难发现,在v1 , v3 , v5 或v2 , v4 , v5各 安置一个也可以,但是只在2个路口安置消 防设施是不行的,所以最少应该安置3个设 施

可以看出,这里实际上要研究的 是用若千个顶点来覆盖图的所有边的 问题。图的覆盖讨论的正是这种关系。 若图G的每条边都至少有一个端点在顶 点集V的一个子集K中,则K称为G的一个覆 盖(Covering)。含顶点个数最少的覆盖称为 最小覆盖,最小、覆盖中所含顶点的个数称为 覆盖数
可以看出,这里实际上要研究的 是用若干个顶点来覆盖图的所有边的 问题。图的覆盖讨论的正是这种关系。 若图G的每条边都至少有一个端点在顶 点集V的一个子集K中,则K称为G的一个覆 盖(Covering)。含顶点个数最少的覆盖称为 最小覆盖,最小覆盖中所含顶点的个数称为 覆盖数