
§3红绿灯的调节 在车辆拥挤的交又路口,需要合理 地调节各车道安置的红绿灯,使车辆能够 顺利、有效地通过。如在下图所示的十字 路口共有6条车道,其中a、b、c、d是4 条直行道,e、f是2条左转弯道,每条车 道都设有红绿灯。要求制定这6组红绿灯 的调节方案
在车辆拥挤的交叉路口,需要合理 地调节各车道安置的红绿灯,使车辆能够 顺利、有效地通过。如在下图所示的十字 路口共有6条车道,其中a、b、c、d是4 条直行道,e、f 是2条左转弯道,每条车 道都设有红绿灯。要求制定这6组红绿灯 的调节方案。 §3 红绿灯的调节

首先应使各道的车辆互不冲突地顺利驶 过路口,其次希望方案的效能尽量地高, 譬如各车道中的绿灯时间最长,使尽可 能多的车辆通过
首先应使各道的车辆互不冲突地顺利驶 过路口,其次希望方案的效能尽量地高, 譬如各车道中的绿灯时间最长,使尽可 能多的车辆通过

月 图1十字路口的6条车道
图1 十字路口的6条车道 d e a b c f

我们的研究对象是6条车道上的 交通流,它们之间的关条由交通流通 过路口时是否相容确定。如C道上的交通流 只与d、f道上的交通流相容。若用图中的 项点表示交通流,当两条交通流相容时将代 表交通流的两顶点连接起来。这样得到的图 称为交通流的相容图。相容图是用图的方法 研究红绿灯调节的基础
我们的研究对象是 6 条车道上的 交通流,它们之间的关系由交通流通 过路口时是否相容确定。如 c 道上的交通流 只与 d、f 道上的交通流 相容。若用图中的 顶点表示交通流,当两条交通流相容时将代 表交通流的两顶点连接起来。这样得到的图 称为交通流的相容图。相容图是用图的方法 研究红绿灯调节的基础

图2就是前面红绿灯调节问题 的相容图。 a o e 图2交通流相容图
a b c d f e 图2 交通流相容图 图2就是前面红绿灯调节问题 的相容图

可行调节 不妨假定6条车道的红绿灯调节是周 期性的,于是只需将每个周期的时问划 分为若干时段,将这些时段作为绿灯时间 分配给各条交通流,使之满足相容性要求。 这相当于对交通流相容图的每个顶点,分 配实轴的上的一个区间,当两个顶点相连 时它们对应的区间才可以重合
不妨假定6条车道的红绿灯调节是周 期性的,于是只需将每个周期的时间划 分为若干时段,将这些时段作为绿灯时间 分配给各条交通流,使之满足相容性要求。 这相当于对交通流相容图的每个顶点,分 配实轴的上的一个区间,当两个顶点相连 时它们对应的区间才可以重合。 可行调节
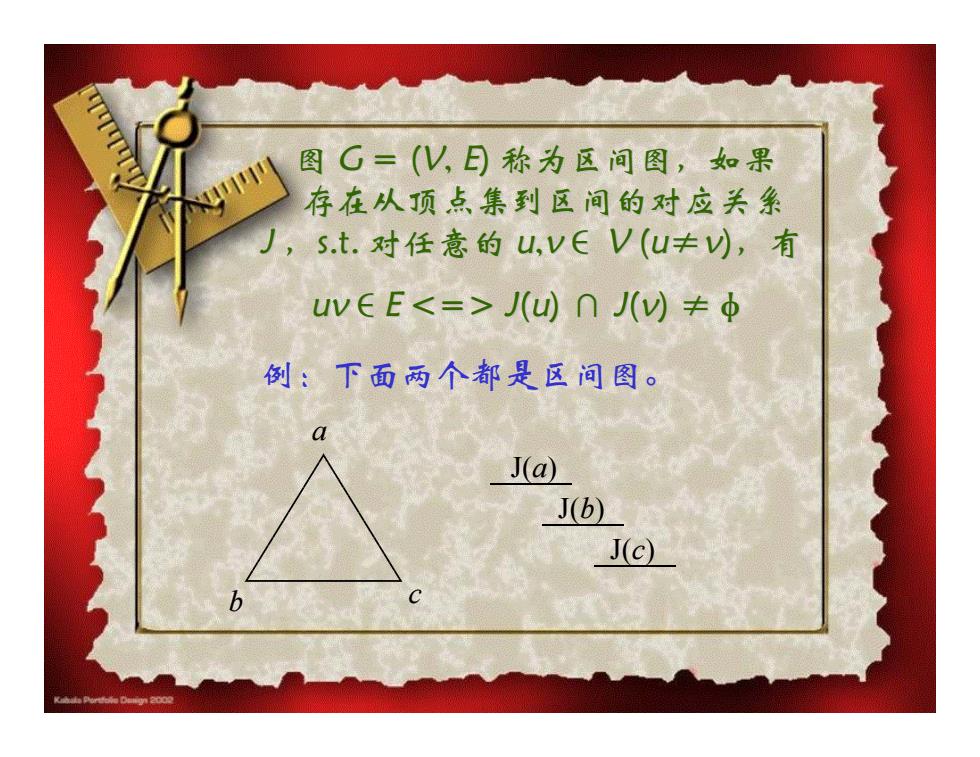
图G=(V,目称为区问图,如果 存在从顶点集到区间的对应关系 s.t.对任意的u,VEV(u≠),有 uv∈EJ(U∩J()≠中 例:下面两个都是区间图。 J(a) J(b) J(c)
图 G = (V, E) 称为区间图,如果 存在从顶点集到区间的对应关系 J ,s.t. 对任意的 u,v∈ V (u≠v),有 uv∈E J(u) ∩ J(v) ≠φ 例:下面两个都是区间图。 a b c J(a) J(b) J(c)
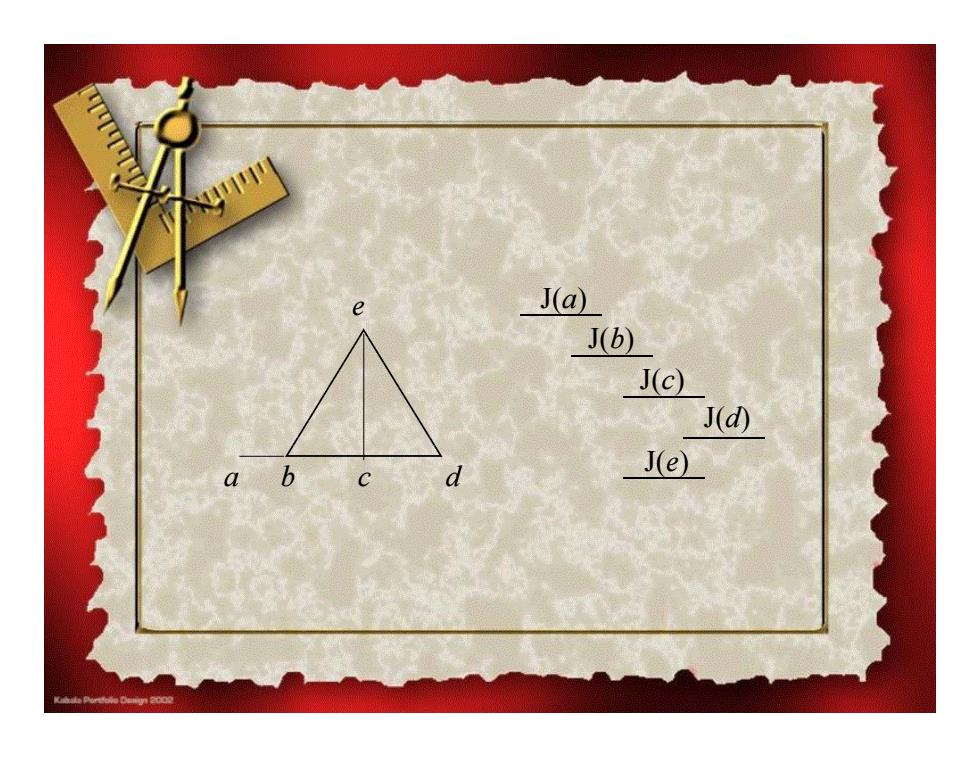
J(a) J(b) J(c) J(d) J(e) 0
e a b c d J( a ) J( b ) J( c ) J( d) J( e )

厅以看出,图2所示的交通流相容图G不 是区间图,但是因为对于相容的交通流, 绿灯时问并不要求一定相重,所以可以去 掉G的某条边,使生成的子图H是区间图
可以看出,图2所示的交通流相容图 G 不 是区间图,但是因为对于相容的交通流, 绿灯时间并不要求一定相重,所以可以去 掉G 的某条边,使生成的子图H 是区间图

图3子图H及对应关系J J(a) J(b) b d J(c) J(d) J(e) J(e)
c d f e a b J(a) J(b) J(c) J(d) J(e) J(e) 图 3 子图 H 及对应关系 J