
第四章方差分析 在工农业生产和科学研究中,经常遇到这样的 问题:影响产品产量、质量的因素很多,我们需要 了解在这众多的因素中,哪些因素对影响产品产 量、质量有显著影响为此,要先做试验,然后对 测试的结果进行分析方差分析就是分析测试结 果的一种方法, ·在方差分析中把在试验中变化的因素称为因 子,用A、B、C、表示因子在试验中所取的不 同状态称为水平,因子A的r个不同水平用A、 A2、、A表示 教学建摸
第四章 方差分析 • 在工农业生产和科学研究中,经常遇到这样的 问题:影响产品产量、质量的因素很多,我们需要 了解在这众多的因素中,哪些因素对影响产品产 量、质量有显著影响.为此,要先做试验,然后对 测试的结果进行分析.方差分析就是分析测试结 果的一种方法. • 在方差分析中,把在试验中变化的因素称为因 子,用A、B、C、...表示;因子在试验中所取的不 同状态称为水平,因子A的r个不同水平用A1、 A2、...、Ar表示
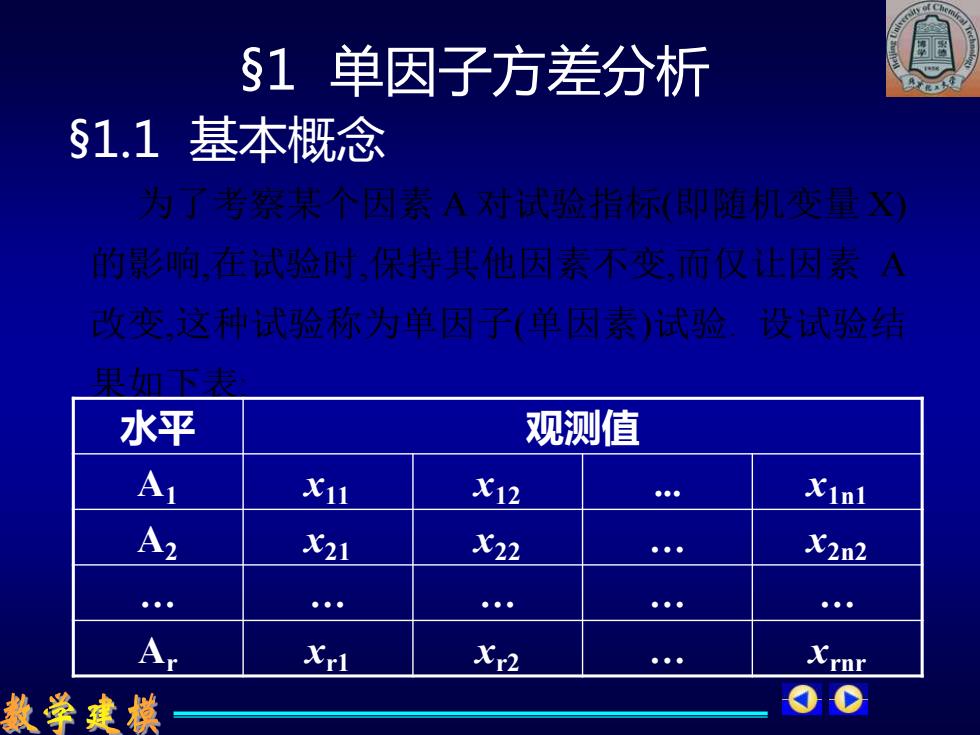
§1单因子方差分析 §1.1基本概念 为了考察某个因素A对试验指标(即随机变量X 的影响,在试验时保特其他因素不变,而仅让因素八 改发变,这种试验称为单因子(单因素)试验。设式验结 水平 观测值 Al X11 X12 X11 A2 X21 X22 ●●。 X2n2 Ar Xrl Xr2 gg● Xrnr 数学建模
§1 单因子方差分析 §1.1 基本概念 为了考察某个因素 A 对试验指标(即随机变量 X) 的影响,在试验时,保持其他因素不变,而仅让因素 A 改变,这种试验称为单因子(单因素)试验. 设试验结 果如下表: 水平 观测值 A1 x11 x12 ... x1n1 A2 x21 x22 … x2n2 … … … … … Ar xr1 xr2 … xrnr
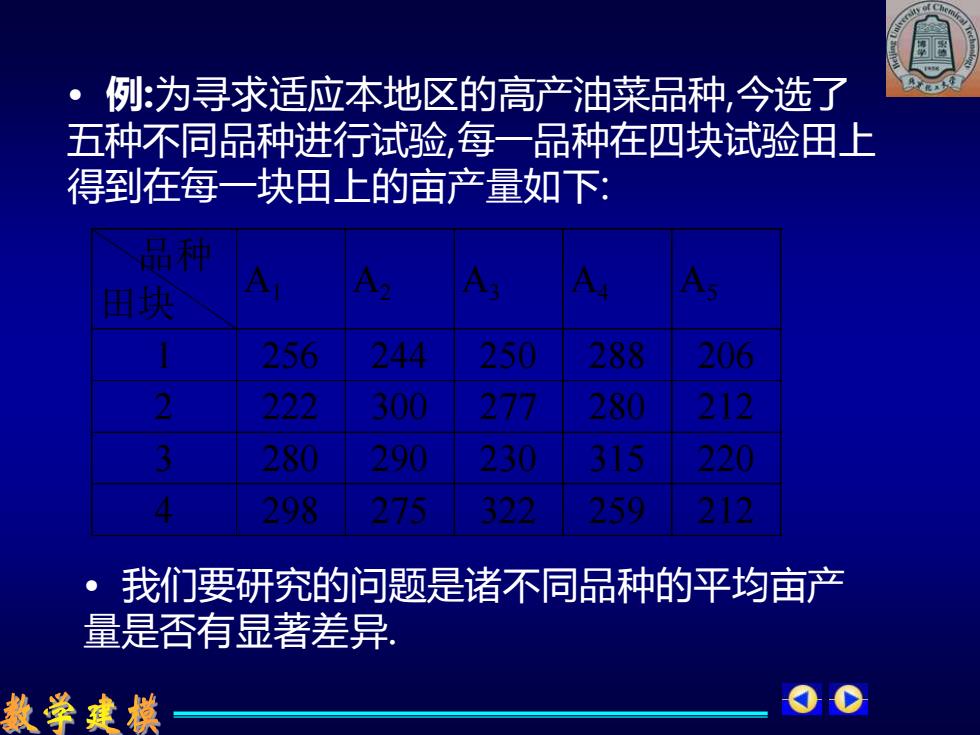
例为寻求适应本地区的高产油菜品种,今选了 五种不同品种进行试验,每一品种在四块试验田上 得到在每一块田上的亩产量如下: 品用 围块 256 244 250 288 206 222 300 27 280 212 280 290 230 31s 220 298 275 22 259 212 我们要研究的问题是诸不同品种的平均亩产 量是否有显著差异 教学建摸
• 例:为寻求适应本地区的高产油菜品种,今选了 五种不同品种进行试验,每一品种在四块试验田上 得到在每一块田上的亩产量如下: 品种 田块 A1 A2 A3 A4 A5 1 256 244 250 288 206 2 222 300 277 280 212 3 280 290 230 315 220 4 298 275 322 259 212 • 我们要研究的问题是诸不同品种的平均亩产 量是否有显著差异

。 在本例中只考虑品种这一因子对亩产量的影响, 五个不同品种就是该因子的五个不同水平由于同 品种在不同田块上的亩产量不同,我们可以认为 个品种的亩产量就是一个总体,在方差分析中总 假定各总体独立地服从同方差正态分布,即第个品 种的亩产量是一个随机变量,它服从分布N(心,σ2), i=1,2,3,4,5. 试验的目的就是要检验假设 H0:1=μ2=μ3=μ4=μ5 是否成立若是拒绝那么我们就认为这五种品种 的平均亩产量之间有显著差异;反之,就认为各品种 间产量的不同是由随机因素引起的方差分析就是 检验假设的一种方法, 数学建摸
• 试验的目的就是要检验假设 H0 :μ1=μ2=μ3=μ4=μ5 是否成立.若是拒绝 ,那么我们就认为这五种品种 的平均亩产量之间有显著差异;反之,就认为各品种 间产量的不同是由随机因素引起的.方差分析就是 检验假设的一种方法. • 在本例中只考虑品种这一因子对亩产量的影响, 五个不同品种就是该因子的五个不同水平.由于同 一品种在不同田块上的亩产量不同,我们可以认为 一个品种的亩产量就是一个总体,在方差分析中总 假定各总体独立地服从同方差正态分布,即第i个品 种的亩产量是一个随机变量,它服从分布N(μi ,σ2 ), i=1,2,3,4,5

。】 实际上,方差分析是检验同方差的若干正态总体均 值是否相等的一种统计方法. ·在实际问题中影响总体均值的因素可能不止一 个我们按试验中因子的个数,可以有单因子方差分 析,双因子分析,多因子分析等例中是一个单因子方 差分析问题 ·设在某试验中,因子A有r个不同水平A1,A2,A 在A水平下的试验结果X服从正态分布 N(,o2),i=1,2,r,且XX2,,X间相互独立.现在 水平A下做了n次试验,获得了n个试验结果 Xj=1,2,n这可以看成是取自X的一个容量为n 的样本,i=1,2r. 教学建模
• 设在某试验中,因子A有r个不同水平A1 ,A2 ,...,Ar , 在Ai水平下的试验结果Xi服从正态分布 N(μi ,σ2),i=1,2,...,r,且X1 ,X2 ,...,Xr间相互独立.现在 水平Ai下做了ni次试验,获得了ni个试验结果 Xij,j=1,2,...,ni这可以看成是取自Xi的一个容量为ni 的样本,i=1,2,...,r. • 实际上,方差分析是检验同方差的若干正态总体均 值是否相等的一种统计方法. • 在实际问题中影响总体均值的因素可能不止一 个.我们按试验中因子的个数,可以有单因子方差分 析,双因子分析,多因子分析等.例中是一个单因子方 差分析问题

。 由于XN(4,σ2)故X与μ的差可以看成一个随机显 误差ε~N(0,σ2).这样一来,可以假定X具有下述数据 结构式: X,=l+c,=1,2,,Ij=1,2,,n1 其中诸εN(0,σ2),且相互独立要检验的假设是 H012=.= ·为了今后方便起见把参数的形式改变一下,并记 24 g=4一 称u为一般平均,Q为因子A的第i个水平的效应: 数学建模
• 由于Xij~N(μi ,σ2 ) ,故Xij与μi的差可以看成一个随机 误差εij~N(0,σ2 ) .这样一来,可以假定Xij具有下述数据 结构式: , 1,2,..., , 1 1 1 i r n n n n i i r i i r i i i = − = = = = = • 为了今后方便起见,把参数的形式改变一下,并记 称μ为一般平均,αi为因子A的第i 个水平的效应. Xij= μi+ εij,i=1,2,...,r;j=1,2,...,ni 其中诸εij~N(0,σ2 ),且相互独立.要检验的假设是 H0 :μ1=μ2=…=μr

在这样的改变下,单因子方差分析模型中的数据 结构式可以写成: =3》)=12月 所要检验的假设可以写成: H0:以1=3=.=,=0 ·为了导出检验假设的统计量,下面我们分析一下 什么是引起诸X波动的原因, 教学建模
• 在这样的改变下,单因子方差分析模型中的数据 结构式可以写成: 所要检验的假设可以写成: i j i i j ni X = + + , i =1,2,...,r; j =1,2,..., H0 :1 = 2 = ... = r = 0 • 为了导出检验假设的统计量,下面我们分析一下 什么是引起诸Xij 波动的原因. = = r i i i n 1 0

§1.2平方和分解公式 。引起诸X:波动的原因有两个:一个是假设H%为真 时,诸X的波动纯粹是随机性引起的;另一个可能是 假设o不真而引起的.因而我们就想用一个量来刻 划诸X之间的波动,并把引起波动的两个原因用另 两个量表示出来,这就是方差分析中常用的平方和 分解法 通常用X,与样本总平均之可的偏差平方种采 反峡X,之间的波动令 其中下= 数学建模
• 引起诸Xij 波动的原因有两个:一个是假设H0为真 时,诸Xij的波动纯粹是随机性引起的;另一个可能是 假设H0不真而引起的.因而我们就想用一个量来刻 划诸Xij之间的波动,并把引起波动的两个原因用另 两个量表示出来,这就是方差分析中常用的平方和 分解法. = = = − r i n j T ij i S X X 1 1 2 ( ) = = = r i n j ij i X n X 1 1 1 其中 反映 之间的波动令 通常用 与样本总平均 之间的偏差平方和来 . i j i j X X X §1.2 平方和分解公式
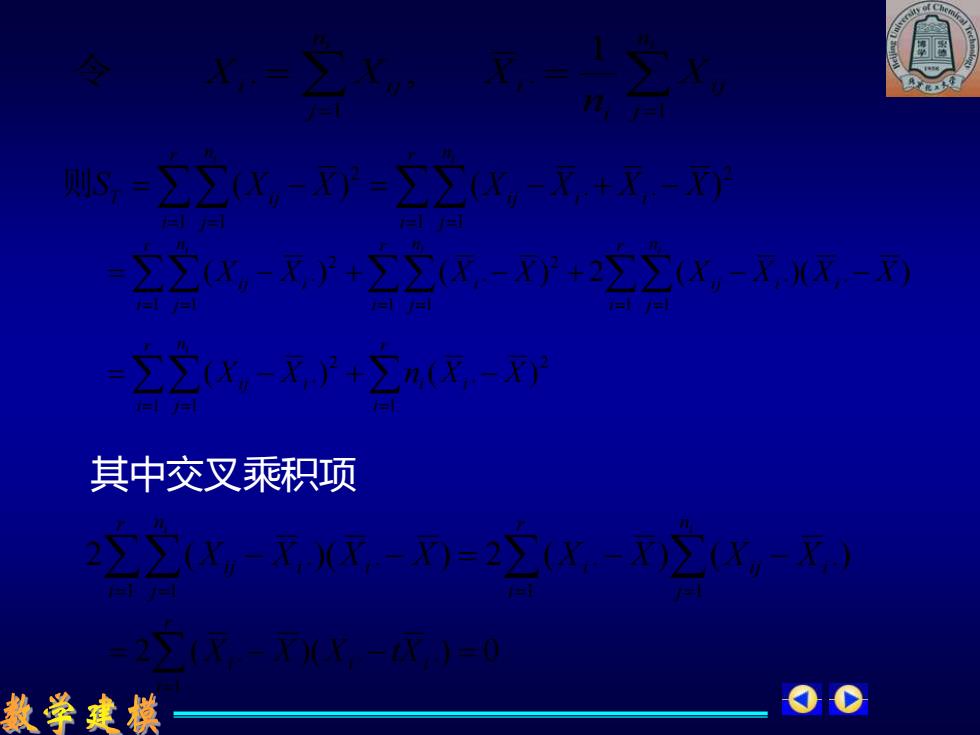
s=】 Σ-=∑-下+了-而 22-y+2=y+2∑∑-以- ∑-元广+∑n8- 其中交叉乘积项 2∑2X,-T,0T-0=22(x-2(W-x) 2Y-T-0= 教学建模
= = = = = − = − + − r i n j i j i i r i n j T i j i i S X X X X X X 1 1 2 1 1 2 则 ( ) ( . . ) 其中交叉乘积项 = = = = − − = − − i ni j i j i r i i i r i n j Xi j Xi X X X X X X 1 1 1 1 2 ( .)( . ) 2 ( . ) ( .) = = = = i ni j i j i i n j i i j X n X X X 1 1 1 令 . , . = = = = − + − r i i i r i n j Xi j Xi n X X i 1 2 2 1 1 ( .) ( . ) 2 ( . )( . .) 0 1 = − − = = i i r i Xi X X tX ( .) ( . ) 2 ( .)( . ) 1 1 1 1 2 1 1 2 X X X X X X Xi X r i n j i j i r i n j i r i n j i j i i i i = − + − + − − = = = = = =

图 22x-8=2n 则S,=S,+S,为一个平厅和分解式 下面我们来看各式的意义 了=一∑∑X,是所有数据的平均值称为总平均值 了,=立x,是从第个总体中拍得的样本平均值称 为组平均值 数学建摸
. ( .) ( . ) 1 2 2 1 1 则 为一个平方和分解式 记 T E A r i A i i r i n j E i j i S S S S X X S n X X i = + = − = − = = = 下面我们来看各式的意义 , . 1 1 1 是所有数据的平均值 称为总平均值 = = = r i n j i j i X n X . , 1 . 1 为组平均值 X 是从第i个总体中抽得的样本平均值 称 n X ni j i j i i = =