北京化工大学2009—2010学年第二学期 《微积分(II)》期末考试试卷 课程代码MAT14700T☐ 班级: 姓名: 学号: 分数: 题号 1 2 3 4 5 6 7 8 9 10 总分 得分 0. 1、求f(x) 的Fourier余弦展开式 0<x<2 第1页
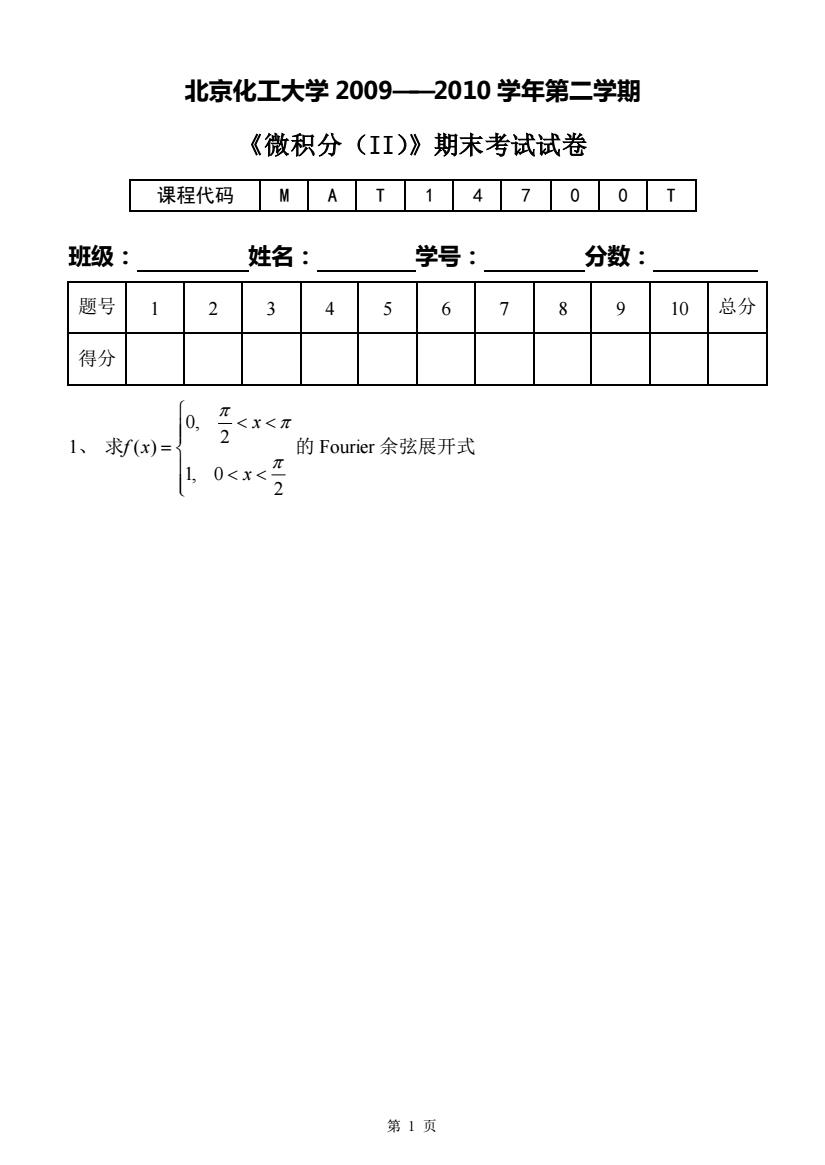
第 1 页 北京化工大学 2009——2010 学年第二学期 《微积分(II)》期末考试试卷 课程代码 M A T 1 4 7 0 0 T 班级: 姓名: 学号: 分数: 题号 1 2 3 4 5 6 7 8 9 10 总分 得分 1、 0, 2 ( ) 1, 0 2 x f x x = 求 的 Fourier 余弦展开式

2、设函数u=x,)具有二阶连续偏导数,求常数a和b,使得在变换5=x+四, 刀=x+y之下,可将方程4。+5,+w+4,+化,=0化为4,=写,试求出这个 解。 第2页
第 2 页 2、 设函数 u u x y = ( , ) 具有二阶连续偏导数,求常数 a 和 b ,使得在变换 = +x ay , = +x by 之下,可将方程 4 5 0 xx xy yy x y u u u u u + + + + = 化为 1 3 u u = ,试求出这个 解

小期们自:-.:2所图区线 第3页
第 3 页 3、 计算 ( ) 2 2 z V e dV x y + ,(V ) 由 2 2 z x y = + , z =1, z = 2 所围成的闭区域

4、计算fds,(C)为球面x2+y2+z2=2与平面x=y的交线。 (C) 第4页
第 4 页 4、 计算 (C) y ds ,(C) 为球面 2 2 2 x y z + + = 2 与平面 x y = 的交线

5、计算2x++:5,(⑨)为平面+皆+异=1,(≥0y20:≥0 第5页
第 5 页 5、 计算 ( ) 4 2 3 S x y z dS + + ,(S ) 为平面 1 2 3 4 x y z + + = ,( x y z 0, 0, 0)

6、设F=0y,-x,),S是锥面:=VF+严上满足0≤x≤1且0≤y≤1部分的下侧。 求「F·d因 S 第6页
第 6 页 6、 设 2 F y x z = − ( , , ) , S 是锥面 2 2 z x y = + 上满足 0 1 x 且 0 1 y 部分的下侧。 求 (S) F dS

入计单禁沙共中)是由点0经直到点Q-3的路径, 为下半圆周,BC是直线。 第7页
第 7 页 7、 计算 ( ) 2 2 4 L xdy ydx x y − + ,其中 (L) 是由点 A( 1,0) − 经点 B(1,0) 到点 C( 1,2) − 的路径, AB 为下半圆周, BC 是直线

8、求常微分方程y+4y=xcosx的通解。 第8页
第 8 页 8、 求常微分方程 y y x x + = 4 cos 的通解

9、求常微分方程组山 =x+2x,-e 的通解。 =4x+3x+4e 第9页
第 9 页 9、 求常微分方程组 1 1 2 2 1 2 2 4 3 4 t t dx x x e dt dx x x e dt − − = + − = + + 的通解

10、求方程y"-xy-y=0在0点附近的幂级数解,并给出收敛范围。 第10页
第 10 页 10、 求方程 y xy y − − = 0 在 0 点附近的幂级数解,并给出收敛范围