
北京化工大学2008一2009学年第一学期 《微积分(I)》期末考试试卷 课程代码MAT14700T 班级: 姓名: 学号: 分数: 题与 123456789101112131415161718 总分 一、填空题(30分) 1、设0,则国 3、函数f(x)=x3-6x2+9x-4在[0,4]上的最大值是 4、m cosf'dr x 5、幂级数艺红-的收敛半径为 6n-3” 6、质数=,a=0在x=0点的1a1or展折式是 二、选择题(40分) 7、设fm在a.上二阶可导,且>0,则F)=f)-f@在(a,b)上 x-a (A)单调增 (B)单调减 (C)有极大值 (D)有极小值 【】 8、设fx)是连续函数,Fx)=f),则F(x)= (A)f(x)+f(-x) (B)f(x)-f(-x)
1 北京化工大学 2008——2009 学年第一学期 《微积分(I)》期末考试试卷 课程代码 M A T 1 4 7 0 0 T 班级: 姓名: 学号: 分数: 题号 一 二 三 总分 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 一、 填空题(30 分) 1、 设 2 2 1 ( ) lim ,( 0) 1 n n n x f x x →+ x − = + ,则 0 lim ( ) x f x → = 2、 1 2 3 1 1 x e dx x = 3、 函数 3 2 f x x x x ( ) 6 9 4 = − + − 在 [0, 4] 上的最大值是 4、 0 2 sin 0 cos lim x x t dt → x = 5、 幂级数 0 ( 3) 3 n n n x n + = − − 的收敛半径为 6、 函数 1 f x a ( ) ,( 0) a x = − 在 x = 0 点的 Taylor 展开式是 二、 选择题(40 分) 7、 设 f x( ) 在 [ , ] a b 上二阶可导,且 f x ( ) 0 ,则 ( ) ( ) ( ) f x f a F x x a − = − 在 (a b, ) 上 (A) 单调增 (B) 单调减 (C) 有极大值 (D) 有极小值 【 】 8、 设 f x( ) 是连续函数, ( ) ( ) x x F x f t dt − = ,则 F x ( ) = (A) f x f x ( ) ( ) + − (B) f x f x ( ) ( ) − −

(D)-f(x)+f-x) (D)-f(x)-f-x) 6、若级数2弘,收敛,且号=1,则级数0, m=l b. (A)收敛 (B)发散 O收敛于空的和 (D)可能收敛,也可能发散 10、设函数1=f)k,1≠0,则1 (A)依赖于s与t (B)依赖于s,不依赖于1 (C)依赖于1,不依赖于s(D)不依赖于s与t 】 11、设函数f(x)=x(x-1(x-2(x-3),则方程f"(x)=0在(0,3)上 (A)没有根 (B)最多有两个根 (C)有且仅有三个根 (D)有四个根 【】 12、设函数f(x)在(0,o)上具有二阶导数,且∫"(x)>0,令4n=f(n,n=1,2,…,则下 列结论正确的是 (A)若>山2,则{u}必收敛(B)若4>4,则{u}必发散 (C)若40,则-(气ar与到=ar) (A)一定相等 (®)当一交a×]存在时相等 (C)一定不等 (D)当(一ar)存在时相等 2
2 (D) − + − f x f x ( ) ( ) (D) − − − f x f x ( ) ( ) 【 】 9、 若级数 1 n n b = 收敛,且 1 1 n n n a b = = ,则级数 1 n n a = (A) 收敛 (B) 发散 (C)收敛于 1 n n b = 的和 (D) 可能收敛,也可能发散 【 】 10、设函数 0 ( ) , 0 s t I t f tx dx t = ,则 I (A) 依赖于 s 与 t (B)依赖于 s ,不依赖于 t (C)依赖于 t ,不依赖于 s (D)不依赖于 s 与 t 【 】 11、设函数 f x x x x x ( ) ( 1)( 2)( 3) = − − − ,则方程 f x ( ) 0 = 在 (0,3) 上 (A) 没有根 (B)最多有两个根 (C) 有且仅有三个根 (D) 有四个根 【 】 12、设函数 f x( ) 在 (0, ) 上具有二阶导数,且 f x ( ) 0 ,令 ( ), 1,2, n u f n n = = ,则下 列结论正确的是 (A) 若 1 2 u u ,则 un 必收敛 (B)若 1 2 u u ,则 un 必发散 (C)若 1 2 u u ,则 un 必收敛 (D)若 1 2 u u ,则 un 必收敛 【 】 13、若 p ,有 lim 0 ( n n p 1 ) n a a + + →+ + + = ,则级数 1 n n a + = (A)收敛 (B) 发散 (C)绝对收敛 (D) 可能收敛,也可能发散 【 】 14、设 1 n n n a x + = 的收敛半径为 R 0 ,则 1 lim n n x R n a x − + → = 与 ( ) 1 lim n n x R n a x − + → = (A)一定相等 (B) 当 1 lim n n x R n a x − + → = 存在时相等 (C)一定不等 (D) 当 ( ) 1 lim n n x R n a x − + → = 存在时相等 【 】

三、解答题(30分) 15、证明:设函数f(x)在0,+)上二阶可导,且f0)>0,∫'(0)<0,∫"(x)≤0,证明:函 数f(x)在[0,+o)上有唯一零点
3 三、 解答题(30 分) 15、证明:设函数 f x( ) 在 [0, ) + 上二阶可导,且 f f f x (0) 0, (0) 0, ( ) 0, 证明:函 数 f x( ) 在 [0, ) + 上有唯一零点
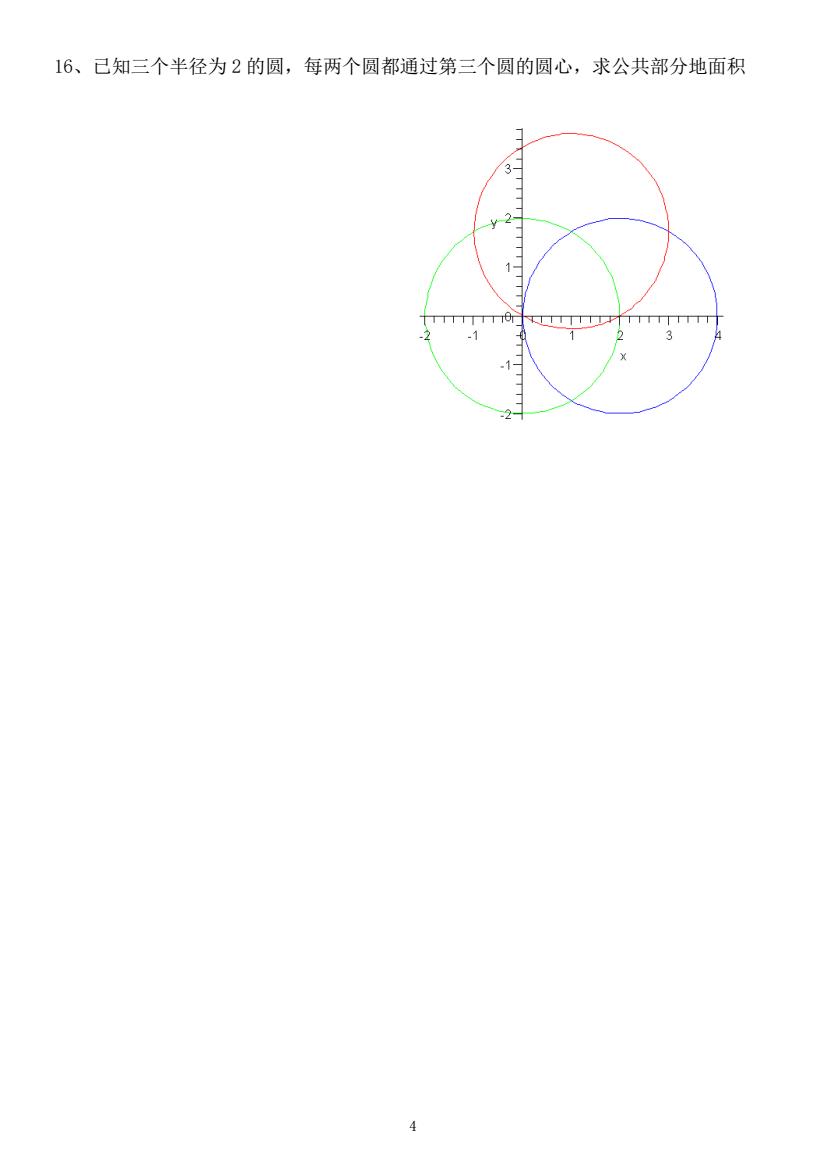
16、已知三个半径为2的圆,每两个圆都通过第三个圆的圆心,求公共部分地面积 3- TTTTTTTT -1 4
4 16、已知三个半径为 2 的圆,每两个圆都通过第三个圆的圆心,求公共部分地面积

17、求方程y-y-y=0在x=0点附近的幂级数解,并给出收敛范围
5 17、求方程 y xy y − − = 0 在 x = 0 点附近的幂级数解,并给出收敛范围

18、求f)=,x在0,2m的Fourier变换展开式,并求宁-)°的和 2 台2n-1 6
6 18、求 ( ) 2 x f x − = 在 [0, 2 ] 的 Fourier 变换展开式,并求 1 1 ( 1) 2 1 n n n + − = − − 的和