
20 第五节B样条曲线 款学建模
第五节 B 样条曲线

在20世纪七十年代初,Gordon.与Riesenfeld等 人在研究了贝塞尔方法以后引入了B样条方法。该方 法具备了贝塞尔方法的一切优点,同时克服了整体 表示的局限,具有局部性质,而且B样条有一套非常 统一、通用、有效的标准算法及强有力的配套技术 (如插入节点、升阶与降阶等),使之成为一种强大 的自由曲线曲面的设计工具。 数学建模
在20世纪七十年代初,Gordon与Riesenfeld等 人在研究了贝塞尔方法以后引入了B样条方法。该方 法具备了贝塞尔方法的一切优点,同时克服了整体 表示的局限,具有局部性质,而且B样条有一套非常 统一、通用、有效的 标准算法及强有力的配套技术 (如插入节点、升阶与降阶等),使之成为一种强大 的自由曲线曲面的设计工具

一.B样条曲线的定义 B样条方法仍采用控制顶点来定义曲线,只不过改用 另一套特殊的基函数。一条n次B样条的曲线方程可 写为: C0)=∑N)P a≤t≤b (6.5.1) P为控制顶点 N,⑦)为p次B样条基函数定义在节点矢量T上 (6.5.2 款学建模
一. B样条曲线的定义 C(t) N (t) Pi a t b n i = i p =0 , 为控制顶点 N (t) i, p 为 次B样条基函数定义在节点矢量T上 = + + − − + 1 1 1 1 , , , , , , , , p p m p p T a a t t b b B样条方法仍采用控制顶点来定义曲线,只不过改用 另一套特殊的基函数。一条n次B样条的曲线方程可 写为: Pi p (6.5.1) (6.5.2)

B样条的其他等价定义 de Boor-Cox递推定义: x日 <t<1 其他 约定0/0=0 0归0 (6.5.3) 第i个k阶B样条N,(),需要用到t,t 共k+1该节点,称区间飞,+]为B样条N() 的支承区间。 数学建模
B样条的其他等价定义 约定0/0=0 i de Boor-Cox递推定义: ( ) = + 0 其他 1 1 ,1 i i i t t t N t ( ) ( ) N (t) t t t t N t t t t t N t i k i k i i k i k i k i i i k 1, 1 1 , 1 1 , + − + + + − + − − − + − − = 第 个 阶B样条 N (t) i,k ,需要用到 i i i k t t t + + , , 1 共 该节点,称区间 i i k t t + , 为B样条 N (t) i,k 的支承区间。 k k +1 (6.5.3)

20 二.B样条曲线的类型划分 (1)均匀B样条曲线 节点矢量中节点为沿参数轴均匀或等距 分布,所有节点区间长度 △,=t4,-1,=c>0,(i=0,1,…,n+k-1 图6.5.1 数学建模·一
二. B样条曲线的类型划分 (1)均匀B样条曲线 节点矢量中节点为沿参数轴均匀或等距 分布,所有节点区间长度 0; ( 0,1, , 1) i = t i+1 −t i = c i = n + k − 图6.5.1
(2)准均匀的B样条曲线 与均匀B样条曲线的差别在于两端节点 具有重复度飞,这样的节点矢量定义了 准均匀的B样条基。 图6.5.2准均匀三次B样条曲线 教学建模
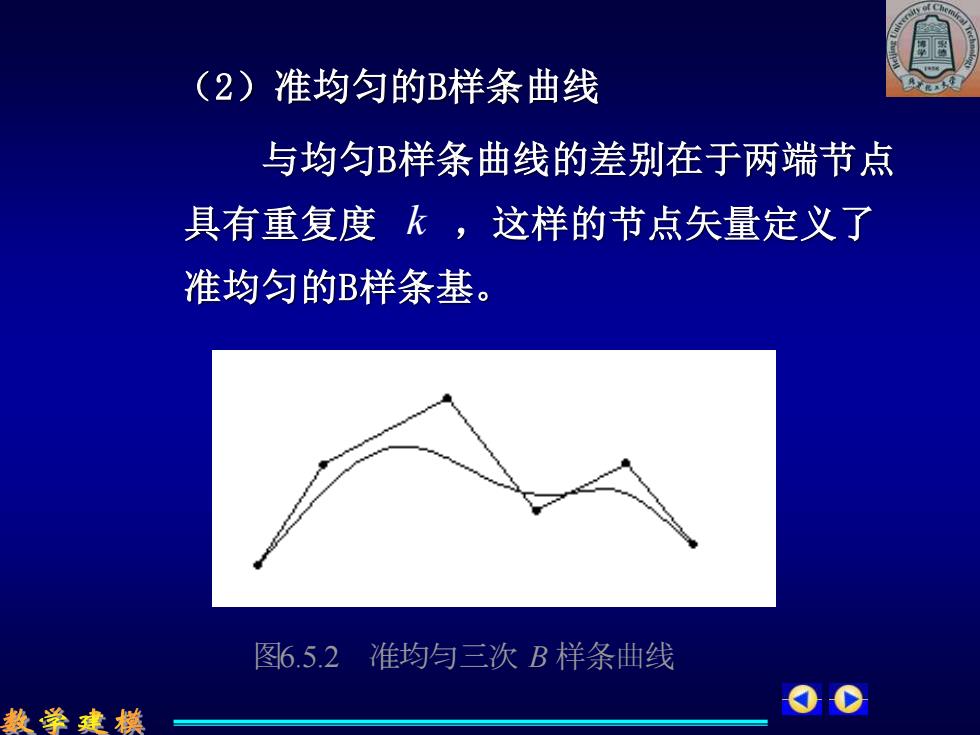
(2)准均匀的B样条曲线 与均匀B样条曲线的差别在于两端节点 具有重复度 ,这样的节点矢量定义了 准均匀的B样条基。 图6.5.2 准均匀三次 B 样条曲线 k
(3)分段Bezierl曲线 节点矢量中两端节点具有重复度飞,所有 内节点重复度为飞-1,这样的节点矢量定义了 分段的Bernstein:基 图6.5.3三次分段Bezier曲线 款学建模
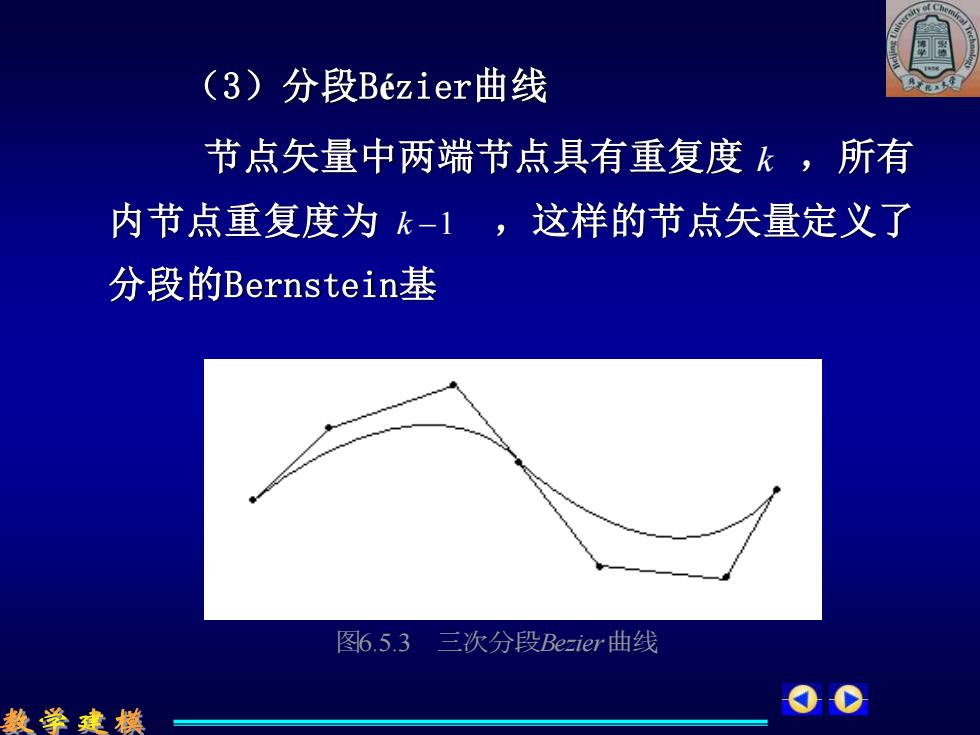
(3)分段Bézier曲线 节点矢量中两端节点具有重复度 ,所有 内节点重复度为 ,这样的节点矢量定义了 分段的Bernstein基 图6.5.3 三次分段Bezier曲线 k −1 k

三.B样条曲线的性质 1.局部性 k阶B样条曲线上参数为t∈[,l]的一点P) 至多与k个控制顶点P=i-k+1,,)有关 2.连续性 Pt)在重节点t,(k≤i≤n),处的连续阶不低于 k-1-r。 整条曲线的连续阶不低于k-1-了m 其中r表示位于区间G,t)内的节点的最 大重数。 数学建模
三. B样条曲线的性质 k −1−r 1.局部性 阶B样条曲线上参数为 1 , i i+ t t t 的一点 P(t) 至多与 个控制顶点 P (j i k i) j = − +1, , 有关 2. 连续性 P(t) 在 重节点 t (k i n) i ,处的连续阶不低于 。整条曲线的连续阶不低于 1 max k − − r 其中 max r 表示位于区间 ( ) 1 1 , k− n+ t t 内的节点的最 大重数。 k k r

3.凸包性 Pt)在区间(G,t),k-1≤i≤n上的部分位于k 个点Pk1,…,P的凸包C,内,整条曲线则位于 各凸包C,的并集Uc,之内。 i=k-1 4.分段参数多项式 P(在每一区间亿,),k-1≤i≤n上都是次数 不高于k-1的参数t的多项式(是参数t 的k一1次分段多项式。 数学建模
3.凸包性 P(t) 在区间 (t i ,t i+1 ),k −1 i n 上的部分位于 个点 Pi k Pi , , − +1 的凸包 Ci 内,整条曲线则位于 各凸包 Ci 的并集 n i k Ci = −1 之内。 4.分段参数多项式 P(t) 在每一区间 (t i ,t i+1 ),k −1 i n 上都是次数 不高于 的参数 的多项式, P(t 是参数 ) 的 次分段多项式。 k k −1 k −1 t t

5.导数公式 由B样条基的微分差分公式,有 PO-x. =∑PN =&-}N0ek】 (6.5.4) 教学建模 00
5. 导数公式 由B样条基的微分差分公式,有 ( ) ( ) ( ) ( ) ( ) , 1 1 1 1 1 1 0 , 0 , 1 , − − + = + + − = = − − = − = = i k k n n i i k i i i n i i i k n i i i k N t t t t t t P P k P N t P t P N t (6.5.4)