
差分方程模型(续) 4差分形式的阻滞增长模型 5按年龄分组的种群增长 数学建模
4 差分形式的阻滞增长模型 5 按年龄分组的种群增长 差分方程模型(续)

问题: 位研究昆虫的生物学家坚持多年到太平洋上 一个远离大陆和其他岛屿的小岛上去考察岛上蝴蝶 的数量变化。多年的抽样统计,发现一个奇怪的现 象:岛上的蝴蝶数量变化很不规律,忽多忽少。 假定岛上蝴蝶的数量只有一种,我们能不能用数 学模型来解释这一现象呢? 敷学建棋
问题: 一位研究昆虫的生物学家坚持多年到太平洋上 一个远离大陆和其他岛屿的小岛上去考察岛上蝴蝶 的数量变化。多年的抽样统计,发现一个奇怪的现 象:岛上的蝴蝶数量变化很不规律,忽多忽少。 假定岛上蝴蝶的数量只有一种,我们能不能用数 学模型来解释这一现象呢?

4差分形式的阻滞增长模型 连续形式的阻滞增长模型(Logistic模型) X0某种群时刻的数量(人)t()=rx(-) t→o,x→N,x=N是稳定平衡点(与r大小无关) 离散 y%某种群第k代的数量(人口) 形式 y-y=y0-.k=12, 若y=N,则+1k+2=Ny=N是平衡点 讨论平衡点的稳定性,即k-→o,y→N? 00 数学建模
( ) (1 ) N x x t = rx − +1 − = (1− ), k =1,2, N y y y ry k k k k 4 差分形式的阻滞增长模型 连续形式的阻滞增长模型 (Logistic模型) t→, x→N, x=N是稳定平衡点(与r大小无关) 离散 形式 x(t) ~某种群 t 时刻的数量(人口) yk ~某种群第k代的数量(人口) 若yk=N, 则yk+1 ,yk+2 ,…=N 讨论平衡点的稳定性,即k→, yk→N ? y *=N 是平衡点

离散形式阻滞增长模型的平衡点及其稳定性 x=0-为0=4gw 变量 代换 x,=G+1)N x4=bx(1-x)(2) 记b=r+1 虫口方程 阶(非线性)差分方程 ()的平衡点=N日2)的平衡点x= r+] 讨论x的稳定性 数学建模
k k y r N r x ( +1) = 记b = r +1 (1 ) (1) 1 N y y y ry k k+ − k = k − 离散形式阻滞增长模型的平衡点及其稳定性 + k+ = + k − k y r N r y r y ( 1) ( 1) 1 1 (1 ) (2) k 1 k k x = bx − x + 一阶(非线性)差分方程 (1)的平衡点y *=N 讨论 x * 的稳定性 变量 代换 (2)的平衡点 r b r x 1 1 1 * = − + = 虫口方程

补充知识 一 阶非线性差分方程x+1=f(x)(I)的平衡点及稳定性 (I)的平衡点x*一代数方程x=x)的根 (1)的近似线性方程 x+1=f(x)+f'(x(x-x)(2 稳定性判断 x*也是(2)的平衡点 f'(x)1x*是(2)和(1)的不稳定平衡点 数学建模
(1)的平衡点 x *——代数方程 x=f(x)的根 稳定性判断 ( ) ( )( ) (2) * * * 1 x f x f x x x k+ = + k − (1)的近似线性方程 x*也是(2)的平衡点 ( ) 1 * f x x*是(2)和(1)的稳定平衡点 ( ) 1 * f x x*是(2)和(1)的不稳定平衡点 补充知识 一阶非线性差分方程 ( ) (1) k 1 k x = f x + 的平衡点及稳定性

x+1=bx,(1一X,)的平衡点及其稳定性 平衡点x=/()=bm1-)x=1-6 b=r+1 另一平衡点为x=0 稳定性 f'(x)=b(1-2x)=2-b f'(0)=b>1 不稳定 /'(x)3/'(x>)日x不稳定 教学建模
( ) (1 2 ) * * f x = b − x ( ) 1 * f x x = f (x) = bx(1− x) (1 ) k 1 k k x = bx − x + 的平衡点及其稳定性 平衡点 b x 1 1 * = − 稳定性 1 b 3 x * 稳定 3 ( ( ) 1) * b f x x * 不稳定 另一平衡点为 x=0 b = r +1 f (0) = b 1 不稳定 = 2 − b

x41=bx:(1一x,)的平衡点及其稳定性 x=bx,(1-x)(2) x=1- b (1)1<b<2 Gx=1-1/b<1/2 =X b/4 x(单调增)x y=f(x) 0 X1x2x1/2 数学建棋
0 y x y = x y = f (x) b / 4 * x 1/ 2 1 0 x 1 x 1 x 2 x (1)1 b 2 1 1/ 1/ 2 * x = − b * x x (单调增) k → (1 ) k 1 k k x = bx − x + 的平衡点及其稳定性 b x 1 1 * xk+1 = bxk (1− xk ) (2) = −
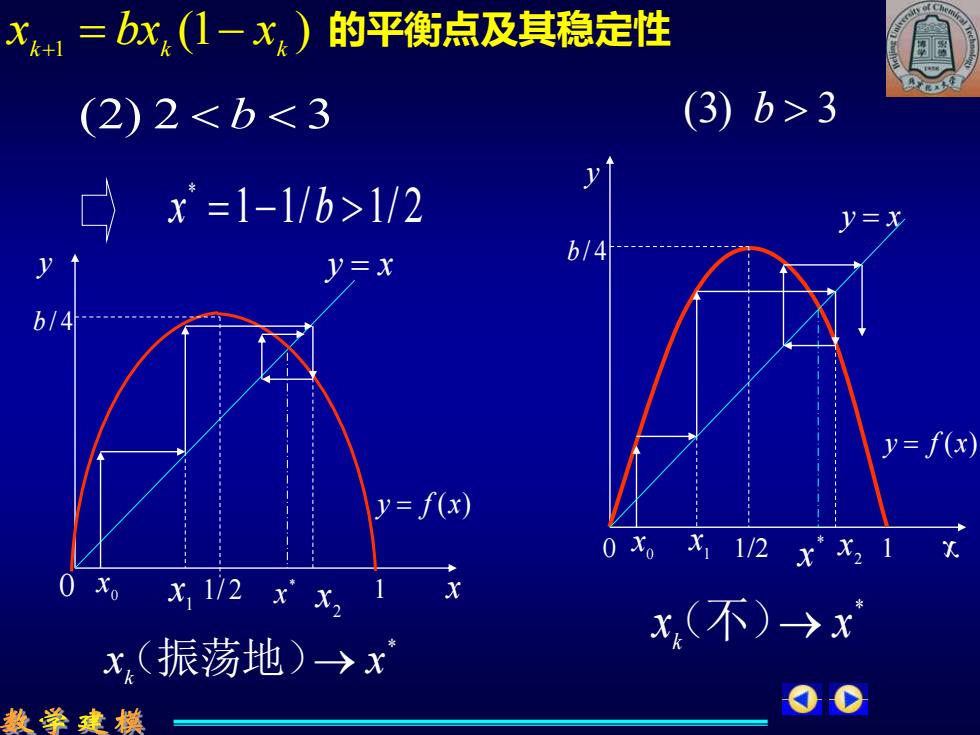
X=bx(1-x) 的平衡点及其稳定性 (2)23 x=1-1/b>1/2 y=x J=x b/4 b/4 y=f(x) y=f(x) O Xo 1/2 x'X2 1 K 0x。x12xx21 x(不)→x x,(振荡地)→x 数学建模 00
(3) b 3 0 1/2 1 y b / 4 y = x y = f (x) 0 x 1 x * x 2 x x (2) 2 b 3 1 1/ 1/ 2 * x = − b * x x (振荡地) k → y 0 x y = x y = f (x) 0 x 1 x 2 x * 1/ 2 x 1 b / 4 * x x (不) k → (1 ) k 1 k k x = bx − x + 的平衡点及其稳定性
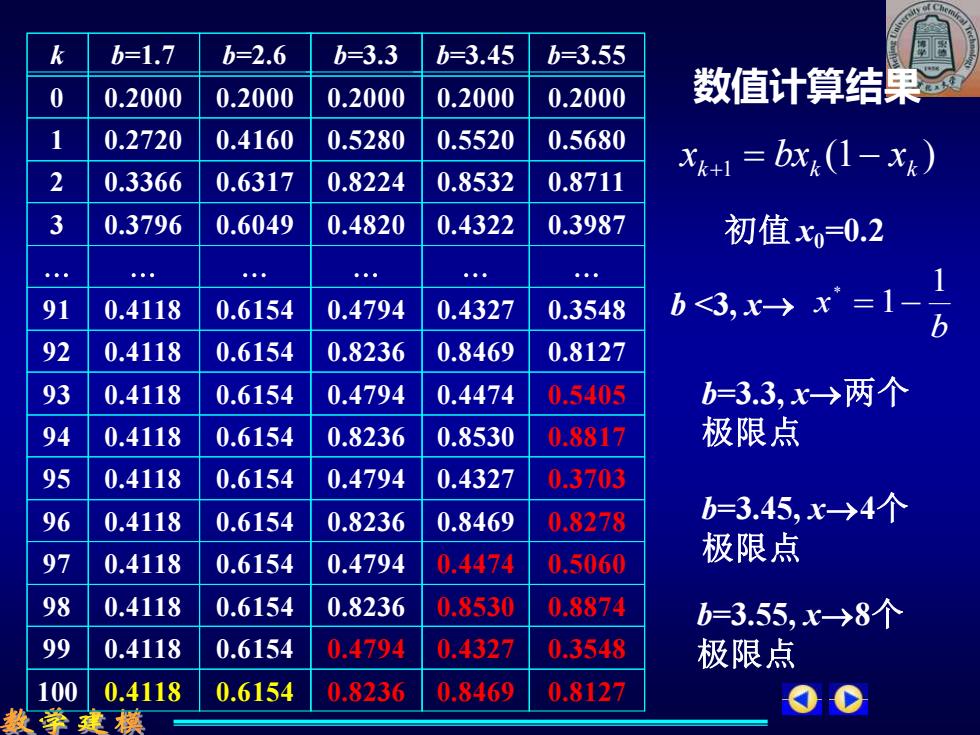
b=1.7 b=2.6 b=3.3 b=3.45 b=3.55 0 0.2000 0.2000 0.2000 0.2000 0.2000 数值计算结果觉 0.2720 0.4160 0.5280 0.5520 0.5680 x+1=bx(1-x) 2 0.3366 0.6317 0.8224 0.8532 0.8711 3 0.3796 0.6049 0.4820 0.4322 0.3987 初值x0=0.2 91 0.4118 0.6154 0.4794 0.4327 0.3548 92 0.4118 0.6154 0.8236 0.8469 0.8127 93 0.4118 0.6154 0.4794 0.4474 0.5405 b=3.3,x-→两个 94 0.4118 0.6154 0.8236 0.8530 0.8817 极限点 95 0.4118 0.6154 0.4794 0.4327 0.3703 96 0.4118 0.6154 0.8236 0.8469 0.8278 b=3.45,x-→4个 97 0.4118 0.6154 0.4794 0.4474 0.5060 极限点 98 0.4118 0.6154 0.8236 0.8530 0.8874 b=3.55,x-→8个 99 0.4118 0.6154 0.4794 0.4327 0.3548 极限点 100 0.4118 0.6154 0.8236 0.8469 0.8127 數学建模
(1 ) k 1 k k x = bx − x + 初值 x0=0.2 数值计算结果 b x 1 1 * b <3, x→ = − b=3.3, x→两个 极限点 b=3.45, x→4个 极限点 b=3.55, x→8个 极限点 100 0.4118 99 0.4118 98 0.4118 97 0.4118 96 0.4118 95 0.4118 94 0.4118 93 0.4118 92 0.4118 91 0.4118 3 0.3796 2 0.3366 1 0.2720 0 0.2000 k b=1.7 0.6154 0.6154 0.6154 0.6154 0.6154 0.6154 0.6154 0.6154 0.6154 0.6154 0.6049 0.6317 0.4160 0.2000 b=2.6 0.8236 0.4794 0.8236 0.4794 0.8236 0.4794 0.8236 0.4794 0.8236 0.4794 0.4820 0.8224 0.5280 0.2000 b=3.3 0.8469 0.4327 0.8530 0.4474 0.8469 0.4327 0.8530 0.4474 0.8469 0.4327 0.4322 0.8532 0.5520 0.2000 b=3.45 0.8127 0.3548 0.8874 0.5060 0.8278 0.3703 0.8817 0.5405 0.8127 0.3548 0.3987 0.8711 0.5680 0.2000 b=3.55

倍周期收敛 一x*不稳定情况的进一步讨论 b=3.3x,(不)→x 子序列X,→X,X241)X 单周期不收敛f(x)=bx1-x) 2倍周期收敛 X41=f(x)x+2=f(x4)=f(f(x》=f2(x)(*) x=f(f(x》=b·bx(1-x[1-bx(1-x] 9的子衡点x=1-分无。-h+1年万-26国 2b x=f(x2),x2=f(x)0<x,<x<x2<1 x*不稳定,研究x1,x2*的稳定性 教学建模
x = f ( f (x))( ), ( ) * 1 * 2 * 2 * 1 x = f x x = f x b b b b x 2 1 2 3 2 * 1,2 + − − = ( ) ( ( )) ( ) (*) (2) k 2 k 1 k k x = f x = f f x = f x + + ( ) k 1 k x = f x + 倍周期收敛——x *不稳定情况的进一步讨论 * x x (不) k → * 2 1 2 * 2 1 x x , x x 子序列 k → k+ → 单周期不收敛 2倍周期收敛 (*)的平衡点 b x 1 1 * = − 0 1 * 2 * * x1 x x x *不稳定,研究x1 * , x2 *的稳定性 f (x) = bx(1− x) = bbx(1− x)[1−bx(1− x)] b = 3.3