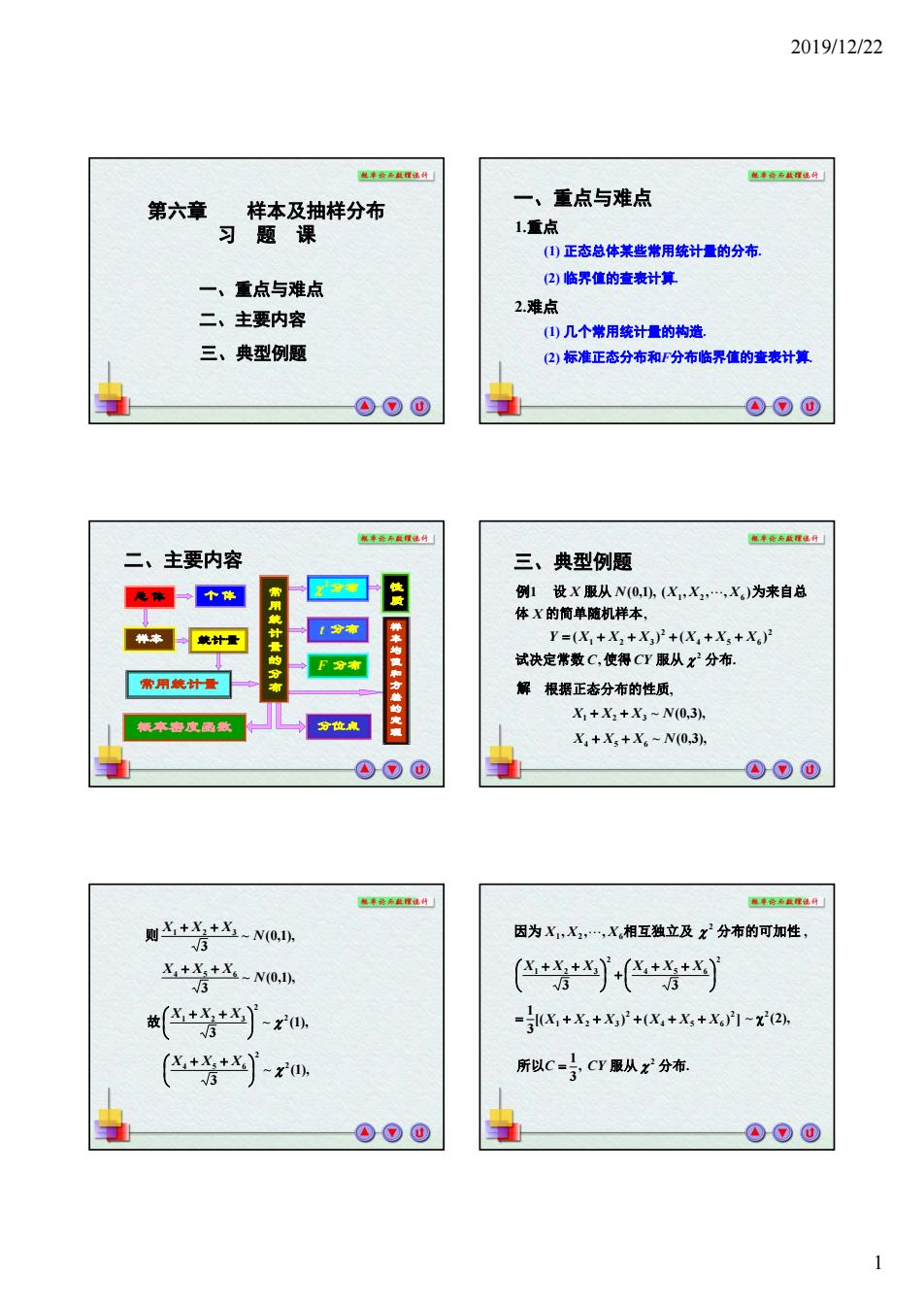
2019/12/22 第六章样本及抽样分布 一、重点与难点 习题课 1.重点 ()正态总体某些常用统计量的分布 一、重点与难点 (②)临界值的查表计算 二、主要内容 2.难点 ()几个常用统计量的构造. 三、典型例题 (2)标准正态分布和F分布临界值的查表计算 ④⊙⊙ 二、主要内容 三、典型例题 一个 例1设X服从N(@,1山,(K,X,,X,)为来自总 体X的简单随机样本, y=X.+X、+X,2+X,+X.+X) 试决定常数C,使得CY服从xX分布, 用装计 F方布 解根据正态分布的性质, 目 X+X2+X2-N0.3. X,+X,+X.-N0,3 ⊙ 0⊙▣ 则++-Na 因为X,X,,X,相互独立及x分布的可加性 -N0. (+*++* 故+告-x0 =X+X,+X,2+X+x+X-x2 (+rm. 所以C=子CY服从x分布. 0⑧0 0⊙0
2019/12/22 1 第六章 样本及抽样分布 习题课 二、主要内容 三、典型例题 一、重点与难点 一、重点与难点 1.重点 (1) 正态总体某些常用统计量的分布. 2.难点 (1) 几个常用统计量的构造. (2) 临界值的查表计算. (2) 标准正态分布和F分布临界值的查表计算. 总 体 个 体 样本 常用统计量的分布 概率密度函数 分位点 二、主要内容 统计量 常用统计量 性质关于样本和方差的定理 t 分布 F 分布 2分布 样本均值和方差的定理 三、典型例题 , . ( ) ( ) , (0,1), ( , , , ) 2 2 4 5 6 2 1 2 3 1 2 6 试决定常数 使得 服从 分布 体 的简单随机样本 设 服从 为来自总 C CY Y X X X X X X X X N X X X 例1 解 根据正态分布的性质, ~ (0,3), X1 X2 X3 N ~ (0,3), X4 X5 X6 N ~ (0,1), 3 1 2 3 N X X X 则 ~ (0,1), 3 4 5 6 N X X X ~ (1), 3 2 2 1 2 3 X X X 故 ~ (1), 3 2 2 4 5 6 X X X , , , , 2 因为 X1 X2 X6相互独立及 分布的可加性 2 4 5 6 2 1 2 3 3 3 X X X X X X [( ) ( ) ] 3 1 2 4 5 6 2 X1 X2 X3 X X X ~ (2), 2 , . 3 所以C 1 CY 服从 2 分布

2019/12/22 为成定使这个本均之 -低同 过。的概率大约为0.01. 1-阁--2-20周-1 懈-)-} 则名--6g) 有(码~49%查标准正态分布表为 于是n=14 新 于是侣≤空x-usa 0Pgs之x-so} -pssx-w'ss aPgs之x-rso =P8≤x16s32 解(山因为X,X,,X是来自正态总体的样本】 =Pz(16)s32)-Piz'(16)s 所以之X-A-xo =1-P%x(16)2321-1-P{x(16281 =0.94 0⊙© ⊙⊙0 抽样分布 a因为2x,--xu-, 分布设X,,X,相互独立,且均服从正态分布N(0, 则称随机变量x=立X服从自由度为m的x分布 于是P侣s空x-Wso} =s2x-rs到 脑机变一服从自由度为的分布,记为-m =P485x15s32y 下分布设D一x(m,bV一xm,U与相互独立,则称 =Px5)28-Px15232 随机变量F=会服从自由度为(%,)的分布, =0.92 0⊙@ 记为F-4 ④⊙@ 2
2019/12/22 2 0.01. , , ( , , , ) ( , , , ) ( , ) 11 12 1 21 22 2 2 1 2 过 的概率大约为 的样本均值 试确定 使得这两个样本均值之 差超 为 的两样本 和 设 和 是来自正态总体 的容量 n n X X X X X X X X N n n 解 ~ , , 2 1 n X N ~ , , 2 2 n X N , 2 ~ 0, 2 1 2 n X X N 则 P{ X1 X2 } 2/ 2 1 2 n n X X P 例2 2/ 2 1 1 2 n n X X P 2 2 1 n n 2 2 2 n 0.01, 0.995, 2 n 有 查标准正态分布表知 2.58, 2 n 于是 n 14. ( ) 2 . 1 2 (2) ( ) 2 ; 1 2 (1) 16 ( , , , ), ~ ( , ), 2 1 2 2 2 1 2 2 1 2 16 2 n i i n i i X X n P X n P n X X X X N 量为 的样本 求概率 设总体 从此总体中取一个容 解 (1) , , , , 因为 X1 X2 X16 是来自正态总体的样本 ( ) ~ ( ), 1 2 1 2 2 X n n i i 所以 例3 2 1 2 2 ( ) 2 1 2 n i Xi n 于是 P ( ) 32 1 8 16 1 2 2 i P Xi {8 (16) 32} 2 P { (16) 32} { (16) 8} 2 2 P P [1 { (16) 32}] [1 { (16) 8}] 2 2 P P 0.94; ( ) ~ ( 1), 1 (2) 2 1 2 2 X X n n i i 因为 2 1 2 2 ( ) 2 1 2 n i Xi X n 于是 P ( ) 32 1 8 16 1 2 2 i P Xi X {8 (15) 32} 2 P { (15) 8} { (15) 32} 2 2 P P 备用例题 0.92 抽样分布 2 分布 ~ ( ). , , , , (0,1) 2 2 2 1 2 2 1 n X n X X N n i i n 记为 则称随机变量 服从自由度为 的 分布 设 相互独立 且均服从正态分布 , t 分布 ~ ( ). ~ (0,1) ~ ( ), 2 n t t t n Y n X t X N Y n X Y 随机变量 服从自由度为 的 分布,记为 设 , 且 与 相互独立,则称 F分布 ~ ( , ). , , ~ ( ) ~ ( ), 1 2 1 2 2 1 2 2 1 2 F F n n n n V n U n F U n V n U V 记为 随机变量 服从自由度为( )的分布 设 , 与 相互独立,则称

2019/12/22 抽样分布d论定理四 能本轮兵融维钱研 两总体样本均值差、样本方差比的分布 能年龄品盐维强研 样本均值的分布 设X,…X与,…,n,分别来自总体V(41,σ)和 设X~N,c2,X,,Xn是来自总体X的样本, N2,c)的样本,且这两个样本相互独立X,T分别 则样本均值有X~N(μ,c2/m).定理四 是这两个样本的样本均值:S,S分别是这两个样本 样本方差、均值的分布 的样本方差,则有 设X,,x是来自总体N(μ,o)的样本,X,S2 分别是样本均值和样本方差,则有 定理四(8) G11σ ~Fm-1,m-1: ()-10s2 ~x2(n-1) (2当a=a=g2时, 定理四(6) 定理四3) --(4-5) (2)X与S独立 (%+%-2) 4-1)S+)S1,1 X-共n-)定理四) ④⊙⑩ %+%2-2 S叶m ④⊙① 3
2019/12/22 3 抽样分布de定理四 样本均值的分布 ~ ( , ). ~ ( , ) , , 2 1 2 X X N n X N X Xn X 则样本均值 有 设 , 是来自总体 的样本, 样本方差、均值的分布 分别是样本均值和样本方差,则有 设 是来自总体 2 的样本, 2 1 X ,, xn N(, ) X, S ~ ( 1) ( 1) (1) 2 2 2 n n S (2) . X与S2 独立 (3) ~ ( 1) t n S n X 定理四(3) 定理四(4) 定理四(1) 两总体样本均值差、样本方差比的分布 1 2 1 2 2 2 112 2 12 1 2 - -( ) ~ ( - 2) ( -1) ( -1) 1 1 - 2 X Y tn n nSnS nn n n 的样本方差,则有 是这两个样本的样本均值; 分别是这两个样本 的样本,且这两个样本相互独立 分别 设 与 分别来自总体 和 2 2 2 1 2 2 2 2 1 1 1 1 , ( , ) . , , , , , ( , ) 1 2 S S N X Y X Xn Y Yn N (2) , ~ ( 1, 1); / / (1) 2 2 2 2 1 2 1 2 2 2 1 2 2 2 1 当 时 F n n S S 定理四(8) 定理四(6)