
例 §6效益的合理分配 甲乙丙三人合作经商,若甲乙合 作获利7元,甲丙合作获利5元,乙丙】 合作获利4元,三人合作获利11元。又知每 人单干获利1元。问三人合作时如何分配获利? 记甲乙丙三人分配为 x=(x,X2,X3) x1+x2+x3=11 解不唯一 x1+x2≥7 (5,3,3) x1+x3≥5 (4,4,3) x2+x3≥4 (5,4,2) X1,X22x3≥1
x1 + x2 + x3 =11 4 5 7 2 3 1 3 1 2 + ³ + ³ + ³ x x x x x x 例 甲乙丙三人合作经商,若甲乙合 作获利7元,甲丙合作获利5元,乙丙 合作获利4元,三人合作获利11元。又知每 人单干获利1元。问三人合作时如何分配获利? 记甲乙丙三人分配为 ( , , ) 1 2 3 x = x x x 解不唯一 (5,3,3) (4,4,3) (5,4,2) , , 1 … … x1 x 2 x 3 ³ §6 效益的合理分配

Shapley合作对策 集合1={1,2,,n 子集s∈I,3实函数v(s)满足 v(φ)=0 v(s Us,)>v(s,)+v(s,)s,Us,= V()~子集的获利 [1,小一n人合作对策,V~特征函数 X=(x1,X2,,xn)~n人从V(0得到的分配,满足 含x=W0 x≥v(i),i=1,2,…,n
( ) 1 x v I n i å i = = x v i i n i ³ ( ), = 1,2,L , f f ³ + = = 1 2 1 2 1 2 ( ) ( ) ( ), ( ) 0 v s s v s v s s s v U U 集合 I = {1,2,L , n} (1) Shapley合作对策 "子集s Î I,$实函数v(s)满足 [ I,v] ~n人合作对策,v~特征函数 ( , , , ) 1 2 n x = x x L x ~n人从v(I)得到的分配,满足 v(s)~ 子集s的获利

Shapley合作对策 公理化方法已 Shapley值 x,=∑w(小[v(s)-v(s,i=1,2 n SES w(5=n-sD1(s-11 n! |5~子集5中的元素数目,5,~包含i的所有子集 [v(s)-v(si)]~i对合作s的“贡献”(i∈s) w(S)~由s决定的“贡献”的权重
! ( )!( 1)! ( ) n n s s w s - - = x w s v s v s i i n Si s i = å ( )[ ( ) - ( \ )], =1,2,L Î 公理化方法 ½s½~子集 s中的元素数目, Si ~包含i的所有子集 w( s ) ~由½s½决定的“贡献”的权重 Shapley值 [v(s) - v(s \ i)] ~ i 对合作s 的“贡献”(i Î s) Shapley合作对策

三人(={1,2,3}》经商中甲的分配X的计算 x1=∑w(sv(s)-v(s1I] S 1 1U2 1U3 us) 17 5 11 Ms\D) 01 1 4 S)-) 16 4 7 s 1 2 23 w(s) 1/31/6 1/6 1/3 w(s)[M(s)-(s\D)] 1/3 2/3 7/3 x=13/3 类似可得2=23/6,x3=17/6
三人(I={1,2,3})经商中甲的分配x1的计算 1/3 1/6 1/6 1/3 w(s)[v(s)-v(s\1)] w(s) s v(s)-v(s\1) v(s\1) v(s) S1 1 1∪2 1 ∪3 I 1 7 5 11 0 1 1 4 1 6 4 7 1/3 1 2/3 7/3 x1=13/3 类似可得 x2=23/6, x3=17/6 ( )[ ( ) ( \ 1)] 1 1 x w s v s v s s S = å - Î 1 2 2 3
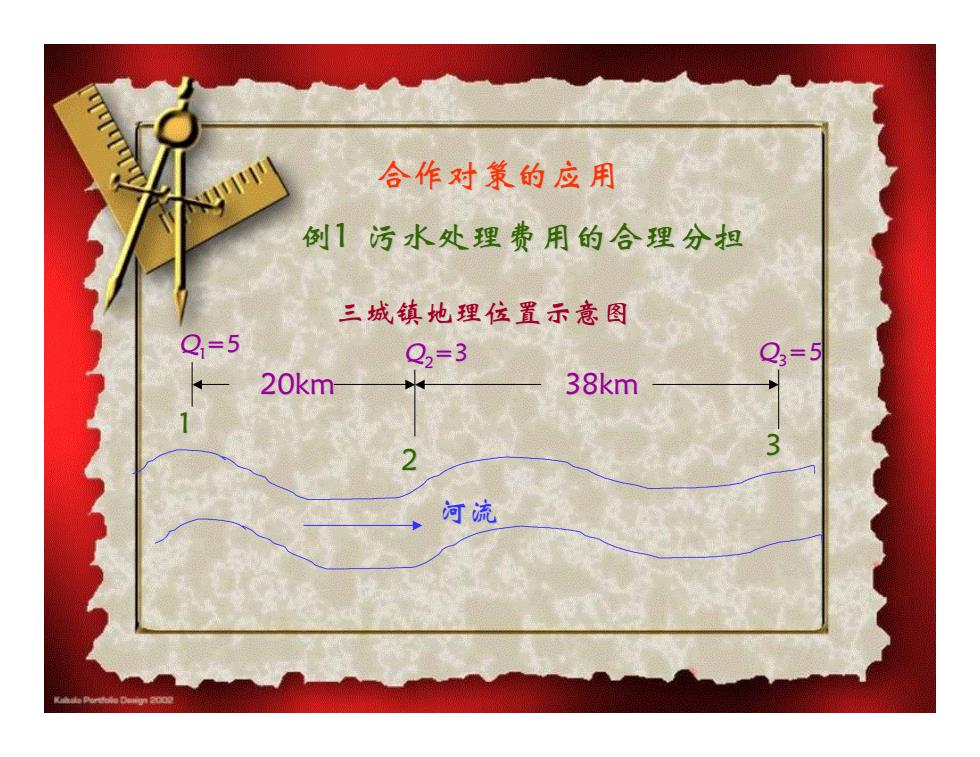
合作对策的应用 例1污水处理费用的合理分担 三城镇地理位置示意图 Q=5 Q2=3 Q3=5 20km 38km 河流
合作对策的应用 例1 污水处理费用的合理分担 20km 38km 河流 三城镇地理位置示意图 1 2 3 Q1=5 Q Q3=5 2=3

污水处理,排入河流 ·三城镇可单独建处理厂,或联合建 厂(用管道将污水由上游城镇送往下 游城镇) Q~污水量,L~管道长度 建厂费用P=73Q0.712 管道费用P2=0.66Q0.51L
•污水处理,排入河流 •三城镇可单独建处理厂,或联合建 厂(用管道将污水由上游城镇送往下 游城镇) Q~污水量,L~管道长度 建厂费用P1=73Q0.712 管道费用P2=0.66Q0.51L

污水处理的5种方案 单独建厂 C(①)=73.572=230,C(2)=160,C(3)=230 总投资D,=C(1)+C(2)+C(3)=620 2)1,2合作 C1,2)=73·(5+3)°72+0.66·51·20=350 总投资D,=C(1,2)+C(3)=580
(1) 73 5 230, (2) 160, (3) 230 0.712 C = × = C = C = (1,2) 73 (5 3) 0.66 5 20 350 0.712 0.51 C = × + + × × = 污水处理的5 种方案 1)单独建厂 总投资 D1 = C(1) + C(2) + C(3) = 620 2)1, 2合作 总投资 D2 = C(1,2) + C(3) = 580

3)2,3合作 C(2,3)=73·(3+5)°72+0.66·351.38=36 总投资D,=C1)+C(2,3)=595 4)1,3合作 C(1,3)=73-(5+5)°72+0.66551.58=463 >C1)+C(3)=460 合作不会实现
(2,3) 73 (3 5) 0.66 3 38 365 0.712 0.51 C = × + + × × = (1,3) 73 (5 5) 0.66 5 58 463 0.712 0.51 C = × + + × × = > C(1) + C(3) = 460 3)2, 3合作 4)1, 3合作 总投资 D3 = C(1) +C(2,3) = 595 合作不会实现

5)三城合作总投资 D,=C1,2,3)=73(5+3+5)72+0.66·51.20 +0.66(5+3)51.38=556 D5最小,应联合建厂 D5如何分担? C①=230 C(2)=160 C3)=230 建厂费:d1=73×(5+3+5)0.712=453 1-→2管道费:d2=0.66×50.51×20=30 2→3管道费:d3=0.66×(5+3)0.51×38=73
0.66(5 3) 38 556 (1,2,3) 73 (5 3 5) 0.66 5 20 0.51 0.712 0.51 5 + + × = D = C = × + + + × × 5)三城合作总投资 D5最小, 应联合建厂 建厂费:d1=73´(5+3+5)0.712=453 1®2管道费:d2=0.66 ´5 0.51 ´20=30 2®3管道费:d3=0.66 ´(5+3)0.51 ´38=73 D5 { D5如何分担? (3) 230 (2) 160 (1) 230 = = = C C C

城3建议 d1按5:3:5分担,d2,d3由城1,2担负 城2建议: d3由城1,2按5:3分担,d2由城1担负 城1计算: 城3分担d×5/13=174C() 意
城3建议: d1 按 5:3:5分担, d2 ,d3由城1,2担负 城2建议: d3由城1,2按 5:3分担, d2由城1担负 城1计算: 城3分担d1´5/13=174C(1) 不 同 意