
北京化工大学2010—2011学年第二学期 《高等数学II》期末考试试卷 课程代码MAT13901T 班级: 姓名: 学号: 分数: 题号 总分 得分 一、填空题(3分×618分) 1.极限..(+y)= 2.函数u= 当x=l,y=e,z=1时的全微分dl= 3.设二元函数z=z(x,y)是由方程x2+z2=xf(y)所确定,其中∫为可微函数, 则 0 4.曲面x2+2y2+z2=12在点(1,1,3)处指向外侧的单位法向量为 5.设2是由曲面z=x2+y2及z=√2-x2-y2所围成的闭区域,将 旷∬f(x+y+)d化成球坐标系下的三次积分是 6.幂级数-5) 的收敛域为 n 第1页
第 1 页 北京化工大学 2010——2011 学年第二学期 《高等数学 II》期末考试试卷 课程代码 M A T 1 3 9 0 1 T 班级: 姓名: 学号: 分数: 题号 一 二 三 总分 1 2 3 4 5 得分 一、填空题(3 分×6=18 分) 1.极限 ( ) ( ) ( ) 1 , 0 , lim 1 x x y a xy → + = 。 2.函数 z y u x = ,当 x =1, y = e , z =1 时的全微分 du = 。 3.设二元函数 z z x y = ( , ) 是由方程 ( ) 2 2 x z x f xy + = 所确定,其中 f 为可微函数, 则 z x = 。 4.曲面 2 2 2 x y z + + = 2 12 在点 (1,1, 3) 处指向外侧的单位法向量为 。 5.设 是由曲面 2 2 z x y = + 及 2 2 z x y = − − 2 所围成的闭区域,将 ( ) 2 2 2 f x y z vd + + 化成球坐标系下的三次积分是 。 6.幂级数 ( ) 1 5 n n x n = − 的收敛域为

二、解下列各题(6分×7=42分) [x=e' 1.设曲线了y= ,一在1=0处的点为P,曲线在点P处与:轴正方向成锐角的切 z=sint 向量为7,求函数u=2+23-在点P处沿方向7的方向导数。 2.设u=f(x,y,),g(x2,y,)=0,y=sinx,其中f和g具有连续的一阶偏导 数,且≠0。试求 du 第2页
第 2 页 二、解下列各题(6 分×7=42 分) 1.设曲线 e 1 1 sin t x y t z t = = − = 在 t = 0 处的点为 P ,曲线在点 P 处与 z 轴正方向成锐角的切 向量为 T → ,求函数 2 3 u xy z xyz = + − 在点 P 处沿方向 T → 的方向导数。 2.设 ( ) ( ) 2 u f x y z g x y z y x = = = , , , , , 0 , sin ,其中 f 和 g 具有连续的一阶偏导 数,且 0 g z 。试求 d d u x
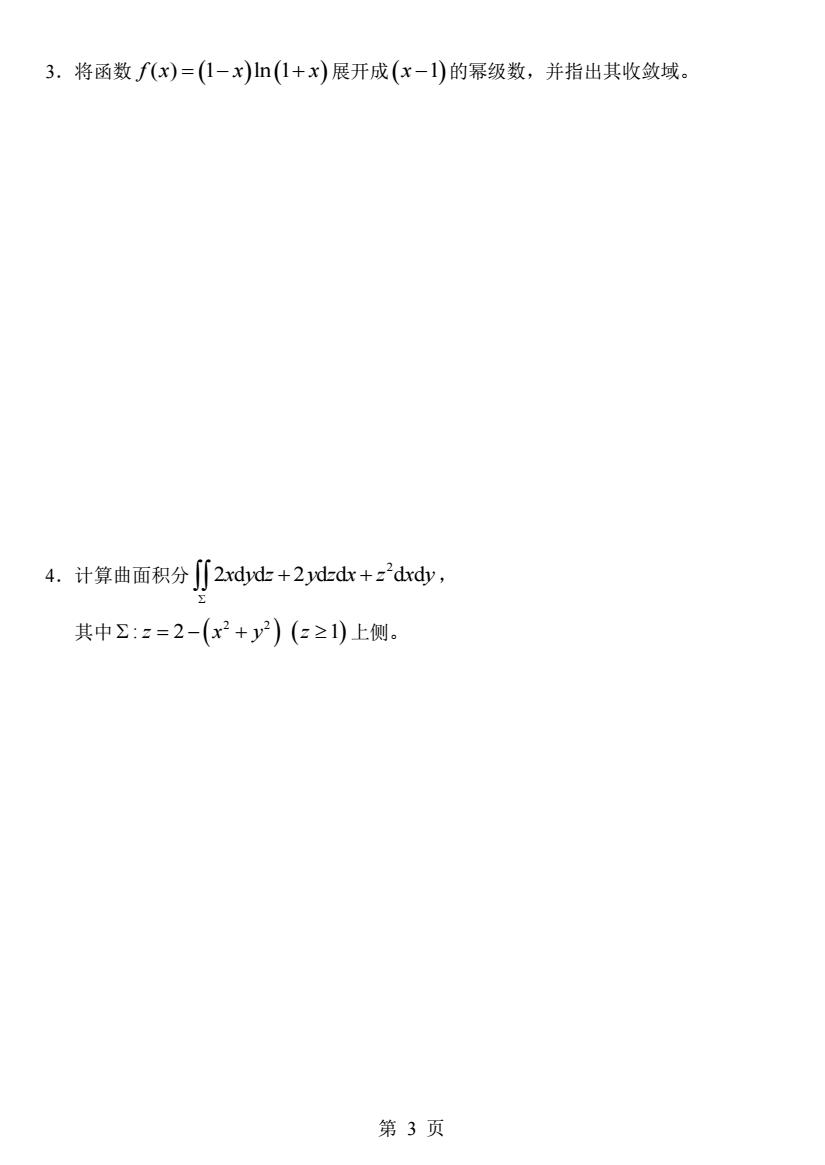
3.将函数f(x)=(1-x)ln(1+x)展开成(x-1)的幂级数,并指出其收敛域。 4.计算曲面积分∬2rdd+2ddr+z2drdy, 其中Σ::=2-(x2+y2)(z≥1)上侧。 第3页
第 3 页 3.将函数 f x x x ( ) 1 ln 1 = − + ( ) ( ) 展开成 ( x −1) 的幂级数,并指出其收敛域。 4.计算曲面积分 2 2 d d 2 d d d d x y z y z x z x y + + , 其中 ( ) ( ) 2 2 = − + : 2 1 z x y z 上侧

5.求幂级数元m的和函数,并计算极限回京.)-27…(6户 6.求微分方程y"-2y'+y=cosx+e的通解。 第4页
第 4 页 5.求幂级数 1 n n nx = 的和函数,并计算极限 ( ) 1 1 1 1 lim 2 4 8 2 3 9 27 3 n n n→ 。 6.求微分方程 '' 2 ' cos ex y y y x − + = + 的通解

7.求力F=(xe2”+)i+(xe2”-y)沿有向曲线L:y=√4x-从原点移动到 A(2,2)点处所作的功。 三、解答下列各题(8分×5=40分) 1.求球面x2+y2+2=2位于第一卦限上一点P,使P点处的切平面与三个坐 标面围成的四面体的体积最小。 第5页
第 5 页 7.求力 ( ) ( ) 2 2 2 e e y y F x y i x y j → → → = + + − 沿有向曲线 2 L y x x : 4 = − 从原点移动到 A(2 , 2) 点处所作的功。 三、解答下列各题(8 分×5=40 分) 1.求球面 2 2 2 2 x y z a + + = 位于第一卦限上一点 P ,使 P 点处的切平面与三个坐 标面围成的四面体的体积最小

2.求由曲面:=x2+y和z=2-√X2+少2所围成的空间体的体积和空间体的上边 界曲面z=2-√x2+y2的表面积。 3.一汽艇以32.4公里/小时的速度在静止的海面上行驶,现在突然关闭其动力系统 它就在静止的海面上作直线滑行,设已知水对汽艇运动的阻力与汽艇运动的速度成 正比,并已知在关闭其动力后20秒汽艇的速度降到10.8公里小时,求汽艇在关闭 动力系统后的运动方程。 第6页
第 6 页 2.求由曲面 2 2 z x y = + 和 2 2 z x y = − + 2 所围成的空间体的体积和空间体的上边 界曲面 2 2 z x y = − + 2 的表面积。 3.一汽艇以 32.4 公里/小时的速度在静止的海面上行驶,现在突然关闭其动力系统, 它就在静止的海面上作直线滑行,设已知水对汽艇运动的阻力与汽艇运动的速度成 正比,并已知在关闭其动力后 20 秒汽艇的速度降到 10.8 公里/小时,求汽艇在关闭 动力系统后的运动方程

π-π≤x≤0 4.将函数f(x)= x0<x≤π 展开成傅里叶级数。 第7页
第 7 页 4.将函数 0 ( ) 0 x f x x x − = 展开成傅里叶级数

.已知曲线积分∫。p(y)d+[e+p(y)]rd与路径无关,其中p(x)可导,且 p(0)=2 1 求:(1)p(x)表达式。 (2)计算从A(0,0)到B(1,)的曲线积分值。 第8页
第 8 页 5.已知曲线积分 ( )d d ( ) y AB − + + y x e y x y 与路径无关,其中 ( ) x 可导,且 ( ) 1 0 2 = 。 求:(1) ( ) x 表达式。 (2)计算从 A(0 , 0) 到 B(1,1) 的曲线积分值