
2010--2011高数(上)期中试题 一、填空(3分×27=81分) 1a-7g-a--, 的定义域为 [1,2] 0≤2x≤4 0≤x≤2 0≤x-1≤41≤x≤51 2.设f(e+1)=e2x+e+x,则f(x)= 令e+l=t,x=ln(t-1) f(t)=(t-1)2+(t-1)+ln(t-1)=t2-t+ln(t-) f(x)=x2-x+In(x-1) x>1
2010----2011高数(上)期中试题 1 0 2 ( ) , ( ) (2 ) ( 1) 2 2 4 x g x f x g x g x x = = + − 1.设 则 的定义域为 2 ( 1) , ( ) x x x 2.设f e e e x f x + = + + = 则 一 、填空(3 27 81 分 = 分) 0 2 4 0 1 4 x x − 0 2 , 1 5 x x [1 2] , 1 , ln( 1) x 令e t x t + = = − 2 2 f t t t t t ( ) (t 1) (t 1) ln( 1) ln( 1) = − + − + − = − + − 2 f x x x x x ( ) ln( 1) 1 = − + −

3.f(x)=-x 在(0,2π)内的第二类间断点是x=π tanx 3 x=二,x=元,x=二π为间断点 2 2 lim- *=o lim-* =0,lim x=0 x→πtan πtanx X 3z tanx X 4.设x-→>0时,(1-cosx)ln(1+x)~(1+ax3)4-1,则a-2 lim (1-cosx)In(1+x) →0 (1+ax3)4-1
0,2 ) tan x f x x x 3. ( )= 在( 内的第二类间断点是 = 3 , , 2 2 x x x = = = 为间断点 x 3 x x 2 2 lim , lim 0, lim 0 tan tan tan x x x x x x → → → = = = 1 3 4 4.设x x x ax a → − + + − = 0 (1 cos )ln(1 ) (1 ) 1, 时, 则 2 1 0 0 3 3 4 1 (1 cos )ln(1 ) 2 2 lim lim 1 1 (1 ) 1 4 x x x x x x a ax ax → → − + = = = + − 2

5.设f(x)=(x-a)g(x),其中g(x)在点a处连续,则f'(a)= (a)-lim ()-(a)=lim(-0 x→a x-a x→a x-a =limg(x)=g(a) x->a 6设y=ntn子,0<x<π,则L dy = -dx 2 tan 2 dy 。dk=d 2 42 tan
5 ( ) ( ) ( ), ( ) ( ) .设f x x a g x g x a f a = − = 其中 在点 处连续,则 ( ) ( ) ( ) lim x a f x f a f a → x a − = − ( ) ( ) 0 lim x a x a g x → x a − − = − lim ( ) x a g x → = 2 6 ln tan ,(0 ), 2 x x y x dy = .设 = = 则 1 1 2 sec 2 2 tan 2 x dy dx x = 2 2 1 1 sec 4 2 tan 4 x dy dx dx = = = = g a( )

7.设y=y(x)油y=x+e确定,则y"(0)=5 y'=1+e(y+xy)当x=0时,y=1y'(0)=2 y"=e"(y+xy)2+e"(r'+y'+xy") y"(0)=1(1+0)2+1(2+2+0)=5 8.设y=(arcsinx)2,则y"(0)= y'=2(arcsinx)〉 一X 1-x2 V1-x2 xarcsinx y"(0)=2 1-x2)月
1 ( ) xy y e y xy = + + . ( ) (0) xy 7设y y x y x e y = = + = 由 确定,则 当x y = = 0 , 1 时 y (0) 2 = 2 ( ) ( ) xy xy y e y xy e y y xy = + + + + 2 y (0) 1(1 0) 1(2 2 0) 5 = + + + + = 5 2 8. (arcsin ) , (0) 设y x y = = 则 2 1 2(arcsin ) , 1 y x x = − 2 2 2 2 1 1 arcsin 1 1 2 1 x x x x x y x − − − − − = − 2 3 2 2 1 arcsin 2 (1 ) x x x x − + = − y (0) 2 =
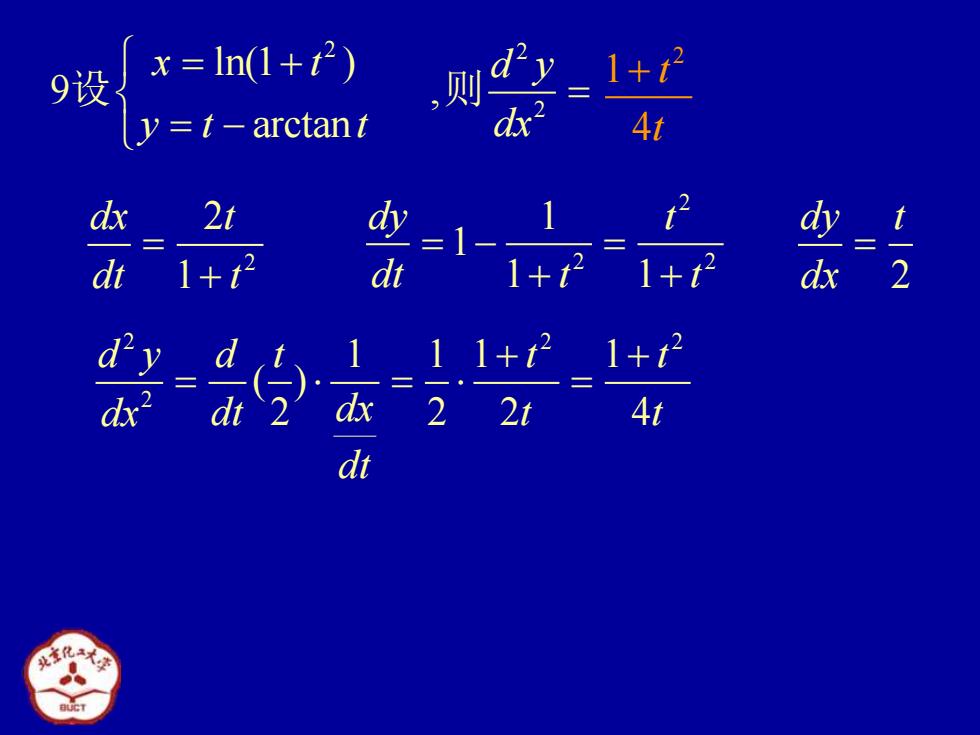
9设 x=In(1+2) ,则y 1+t y=t-arctant dx At dx 21 1+2 =1-+ 1+ t-2 k221-4t dt
2 2 2 ln(1 ) 9 , arctan x t d y y t t dx = + = = − 设 则 2 2 1 dx t dt t = + 2 2 2 1 1 1 1 dy t dt t t = − = + + 2 dy t dx = 2 2 2 2 1 1 1 1 ( ) 2 2 2 4 d y d t t t dx dt t t dx dt + + = = = 2 1 4 t t +

10.设曲线y=fx)与y=snx在原点相切,则mW(白= 1>00 两个函数在(0,0)切线斜率相同 f'0)=cos0=1,且f0)=0 f0+分)-f0) n .2=2f(0)=2 n→ 2 n 11.y=a*+sin3x(a >0)y(m)= yo=aaar+3”sin3x+n7
2 10. ( ) sin lim ( ) n y f x y x nf → n 设曲线 = = = 与 在原点相切,则 两个函数在(0 0,)切线斜率相同 f f (0) cos0 1 (0) 0 = = = ,且 2 (0 ) (0) 2 lim ( ) lim 2 n n 2 f f n nf n n → → + − = 2 (0) 2 f + = = ( ) 11. sin3 ( 0), x n y a x a y = + = 则 ( ) (ln ) 3 sin(3 ) 2 n x n n y a a x n = + +

12.函数f(x)=二按(x+1)的幂展开的带有拉格朗日 X 余项的二阶泰勒公式为 =京r-3/= f(-1)=-1,f'(-1)=-1,f"(-1)=-2 -1-(x*)-e++Xx+ =-1-(+)-+-京+y 5在-1与.x之间
1 12 ( ) 1 f x x x .函数 = + 按( )的幂展开的带有拉格朗日 余项的二阶泰勒公式为 2 3 4 1 2 3! f x f x f x ( ) , ( ) ( ) x x x = − = = − , f f f ( 1) 1, ( 1) 1, ( 1) 2 − = − − = − − = − 2 3 4 1 1 3! 1 ( 1) ( 1) ( )( 1) 3! x x x x = − − + − + + − + 2 3 4 1 1 ( 1) ( 1) ( 1) x x x = − − + − + − + 在−1与x之间

13.函数y=xx(x>0)在区间(e,+∞)上是单调减少, 极值点是x=e Iny=-Inx y'1-Inx y -x=(1-Inx) y=y- 令y=0,得x=e x>e,y'0x=e取极大值
1 3 ( 0) x 1 .函数y x x = 在区间 上是单调减少, 极值点是 1 ln ln y x x = 2 y x 1 ln y x − = 1 2 2 1 ln (1 ln ) x x y y x x x − − = = − 令y x e = = 0,得 x e y , 0 x e y , 0 x e = 取极大值 (e,+ ) x e =

14.函数y=arctane在区间(-o,0)上是凹的,拐点是 -y--) 0+e2x2- 1+e2x2 y”=0,x=0 x0,曲线是凹的
14 arctan x .函数y e = 在区间 上是凹的,拐点是 2 2 2 2 2 2 2 2 (1 ) 2 (1 ) , y 1 (1 ) (1 ) x x x x x x x x x x e e e e e e e y e e e + − − = = = + + + ( ,0) − y x = = 0, 0 0, 0 x y ,曲线是凹的 (0, ) 4 0, 4 x y = =

15.函数y=lnx在与x轴交点处的曲率为 切线方程为 y=0,x=1 (1)=1,y(1)=-1 12 0+y29 22 4 切线方程为y-0=1(x-1) 即x-y-1=0
15 ln .函数y x x = 在与 轴交点处的曲率为 , 切线方程为 2 1 1 y y, x x = = − y x = = 0, 1 y y (1) 1, (1) 1 = = −3 2 2 | | 1 2 2 2 4 (1 ) y K y = = = + 切线方程为y x − = − 0 1( 1) 即x y − − =1 0