
微分中值定理及其应用
微分中值定理及其应用
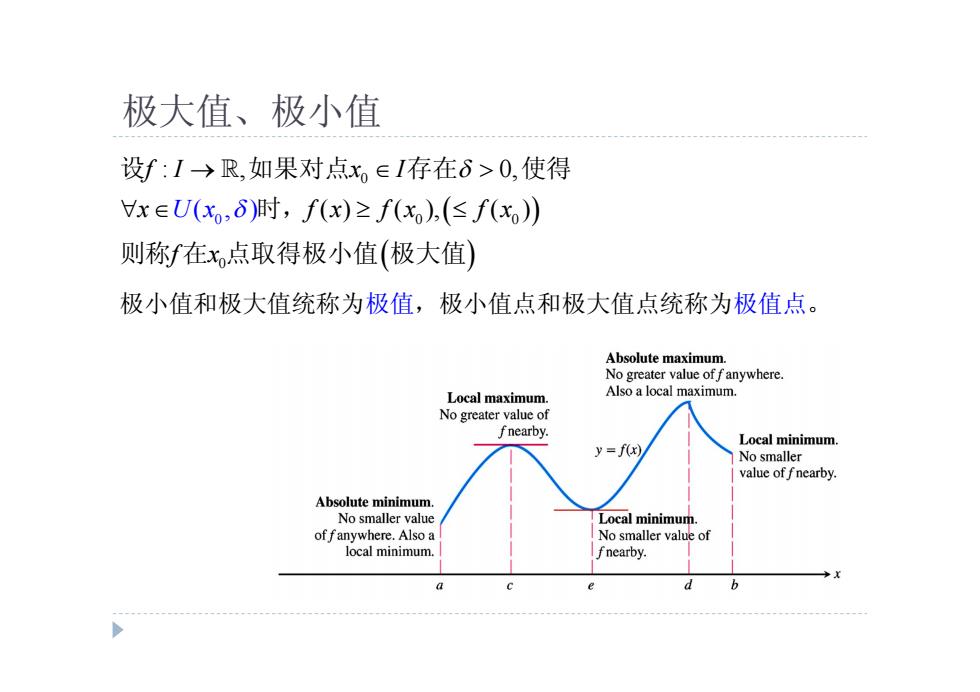
极大值、极小值 设f:I→R,如果对点x,∈I存在6>0,使得 x∈U(x,δ)时,f(x)≥f(x),(≤f(x) 则称f在x点取得极小值(极大值) 极小值和极大值统称为极值,极小值点和极大值点统称为极值点。 Absolute maximum. No greater value of fanywhere. Local maximum. Also a local maximum. No greater value of fnearby. Local minimum. =f(x) No smaller value of fnearby. Absolute minimum. No smaller value Local minimum. of fanywhere.Also a No smaller value of local minimum. nearby
极大值、极小值 0 0 0 0 0 : , 0, U( , ) ( ) ( ), ( ) f I x I x f x f x f x f x x 设 如果对点 存在 使得 时, 则称 在 点取得极小值 极大值 极小值和极大值统称为极值,极小值点和极大值点统称为极值点
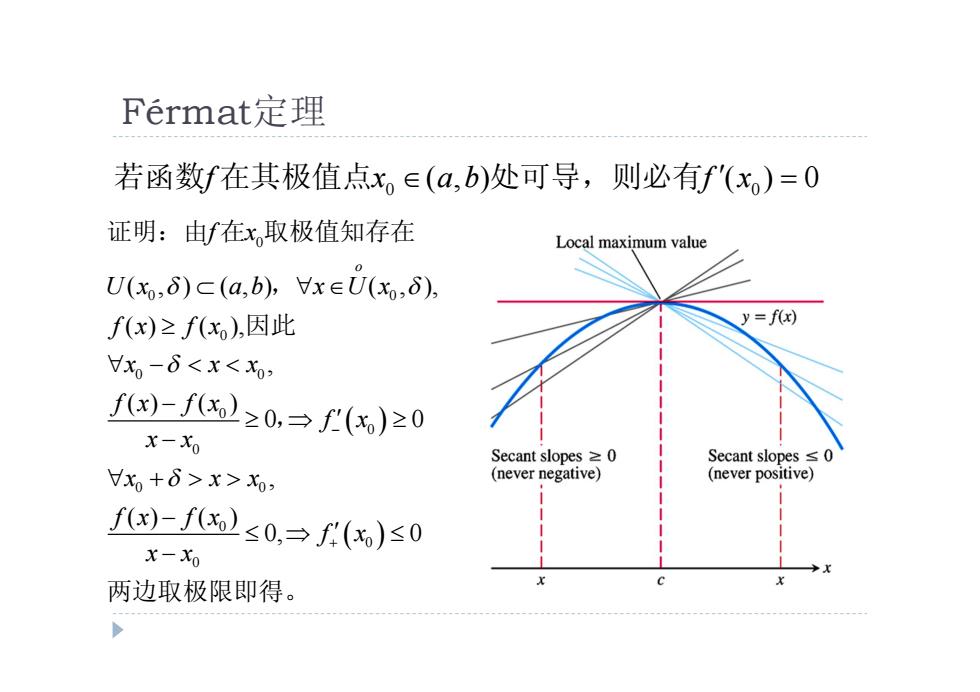
Fermat定理 若函数f在其极值点x。∈(a,b)处可导,则必有f'(x)=0 证明:由f在x,取极值知存在 Local maximum value UJ(x,δ)c(a,b),x∈U(x,δ), f()≥f(x),因此 y=f(x) x。-6x>, (never negative) (never positive) fx)-f≤0,→f(x)≤0 x-Xo 两边取极限即得
Férmat定理 0 0 若函数f x a b f x 在其极值点 ( , ) ( ) 0 处可导,则必有 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ( , ) ( , ) ( , ), ( ) ( ), , ( ) ( ) 0 0 , ( ) ( ) 0, 0 o f x U x a b x U x f x f x x x x f x f x f x x x x x x f x f x f x x x 证明:由 在 取极值知存在 , 因此 , 两边取极限即得

Fermat,Pierre de (1601--1665) 费马法国数学家,任职律师。自1631年起任图卢滋 议会议员。任职期间,他利用工余时间钻研数学, 费马生前性情淡泊,为人谦逊,他不发表著作, 而是在书的边缘上写下一些草率的注记或者偶尔 把他的发现写信告诉他的朋友。后来还是由他的 儿子于I679年把这些造作整理汇集成书《Varia Opera>》共两卷,在图卢兹出版。因为如此的习惯, 他失掉了发现解析几何的优先权。也丢掉了发明 微积分的某些特性的优先权,这些特性后来启发 了牛顿发明了微积分。费马对数论尤其钟爱,他 是近代“数论”的真基者。另外,他也是早期微 积分学的先驱。他于1636年给罗贝瓦尔及1638年 给笛卡儿的信中提出求极大、极小与拐点的步骤, 实际已相当于使导数成零而求极点之方法。这成 为现代微积分中函数取极值之必要条件。而且, 他曾讨论曲线xmyn=k(m,n是正整数)下的面积, 并通过求和过程得到求曲线所围面积之公式此外, 他透过与帕斯卡之通信讨论赌全分配问题,得出 正确解答,因而成为7世纪兴起的概率论的共同 创立者之一。他还于光学研究中提出「费马原 理」,给后世变分法之研究极大的启示
Fermat, Pierre de (1601--1665) 费马法国数学家,任职律师。自1631年起任图卢兹 议会议员。任职期间,他利用工余时间钻研数学. 费马生前性情淡泊,为人谦逊,他不发表著作, 而是在书的边缘上写下一些草率的注记或者偶尔 把他的发现写信告诉他的朋友。后来还是由他的 儿子于1679年把这些遗作整理汇集成书《Varia Opera》共两卷,在图卢兹出版。因为如此的习惯, 他失掉了发现解析几何的优先权。也丢掉了发明 微积分的某些特性的优先权,这些特性后来启发 了牛顿发明了微积分。费马对数论尤其钟爱,他 是近代“数论”的奠基者。另外,他也是早期微 积分学的先驱。他于1636年给罗贝瓦尔及1638年 给笛卡儿的信中提出求极大、极小与拐点的步骤, 实际已相当于使导数成零而求极点之方法。这成 为现代微积分中函数取极值之必要条件。而且, 他曾讨论曲线x m y n = k(m,n是正整数)下的面积, 并通过求和过程得到求曲线所围面积之公式.此外, 他透过与帕斯卡之通信讨论赌金分配问题,得出 正确解答,因而成为17世纪兴起的概率论的共同 创立者之一。他还于光学研究中提出「费马原 理」,给后世变分法之研究极大的启示
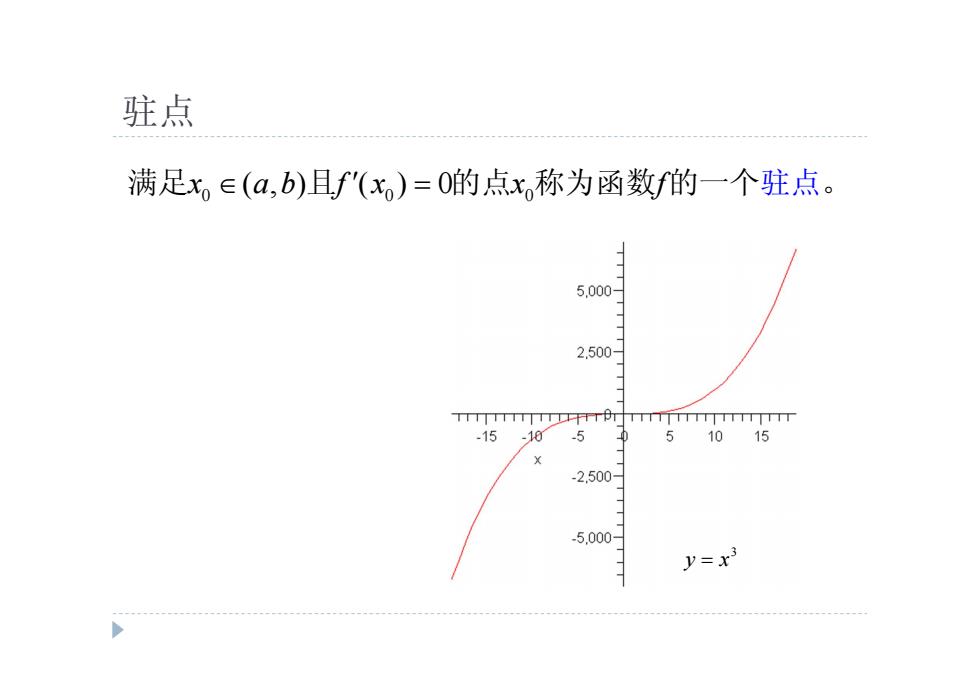
驻点 满足x。∈(a,b)且f'(x)=0的点x称为函数f的一个驻点。 5.000 2.500- TnmnTDrpnmnnr -15 -10 5 1015 -2.500 -5.000- y=x3
驻点 0 0 0 满足x a b f x x f ( , ) ( ) 0 且 的点 称为函数 的一个驻点。 3 y x

Rolle定理 若函数f在a,b]上连续,在(a,b)内可导,f(a)=f(b),则归5∈(a,b) 使得f'(5)=0 证明:记f在[a,b]上的最大最小值分别为M,m,如果M=m,则f为常值 函数,定理显然成立。如果M≠m,由于f(a)=f(b),所以M与m必然 有一个在(a,b)内达到,定理得证
[ , ] ( , ) ( ) ( ), ( , ) ( ) 0 f a b a b f a f b a b f 若函数 在 上连续,在 内可导, 则 使得 [ , ] , , , , ( ) ( ) ( , ) f a b M m M m f M m f a f b M m a b 证明:记 在 上的最大最小值分别为 如果 则 为常值 函数,定理显然成立。如果 由于 ,所以 与 必然 有一个在 内达到,定理得证。 Rolle定理

Rolle,Michel 罗尔是法国数学家,1652年4月21日生于昂贝尔特, I719年1川月8日辛于巴黎。 罗尔在数学上的成就主要是在代数方面,专长于丢香 图方程的研究。罗尔于9!年在题为《任意次方程的 一个解法的证明》的论文中指出了:在多项式方程的 两个相邻的实根之间,方程至少有一个根。在一百多 年后,I846年尤斯托(Giusto Bellavitis)将这一定理推 广到可微函数,尤斯托还把此定理命名为罗尔定理。 The calculus is a collection of ingenious fallacies
Rolle,Michel 罗尔是法国数学家,1652年4月21日生于昂贝尔特, 1719年11月8日卒于巴黎。 罗尔在数学上的成就主要是在代数方面,专长于丢番 图方程的研究。 罗尔于1691年在题为《任意次方程的 一个解法的证明》的论文中指出了:在多项式方程 的 两个相邻的实根之间,方程 至少有一个根。在一百多 年后,1846年尤斯托(Giusto Bellavitis)将这一定理推 广到可微函数,尤斯托还把此定理命名为罗尔定理。 The calculus is a collection of ingenious fallacies

例 证明方程x3+2x+1=0在区间(-1,0)内有且只有一个实根。 证明若函数f:[0,→R在[0,]上连续,在(0,1)内可导,并且 f四=0,则至少存在一个ce(0,1),f(c)=-f
例 3 证明方程x x 2 1 0 1,0 在区间 内有且只有一个实根。 : 0,1 0,1 0 1 (1) 0 0,1 , f f c f c f c c 证明若函数 在 上连续,在 ,内可导,并且 ,则至少存在一个
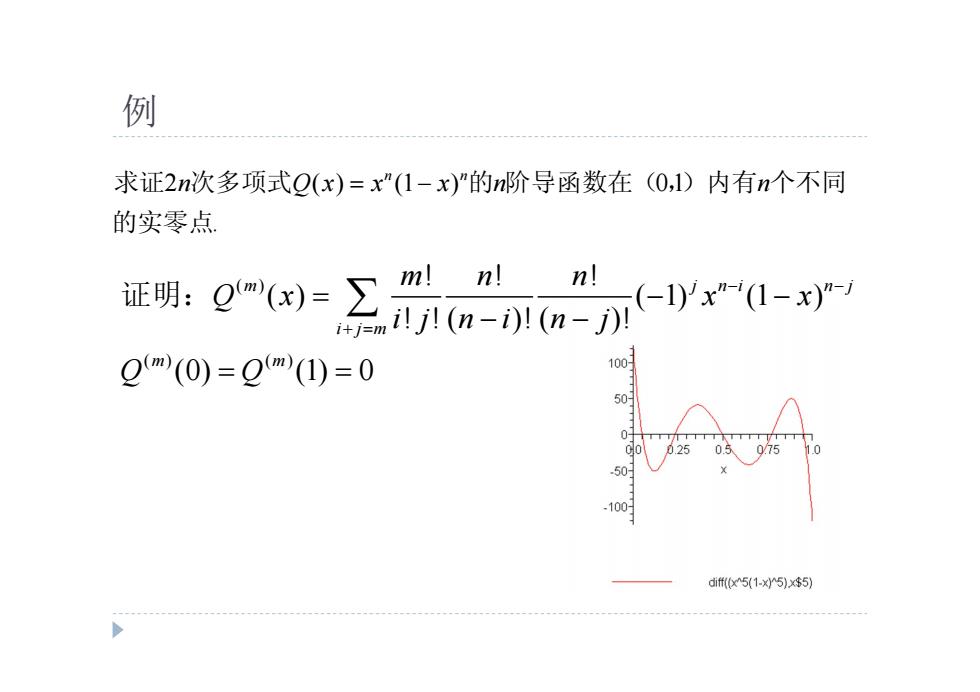
例 求证2n次多项式Q(x)=x"(1-x)”的n阶导函数在(0,l)内有n个不同 的实零点 m! n! t明:e(三a”anr1- n! 2m(0)=Qm(1)=0 100时 50 50 .100 df0x5(1-x05)x$5)
例 2 ( ) (1 ) 0 1 . n n 求证 n Q x x x n n 次多项式 的 阶导函数在( ,)内有 个不同 的实零点 ( ) ( ) ( ) ! ! ! ( ) ( 1) (1 ) ! ! ( )! ( )! (0) (1) 0 m j n i n j i j m m m m n n Q x x x i j n i n j Q Q 证明:

Lagrange中值定理 若函数f在[a,b]上连续,在(a,b)内可导,则归c∈(a,b), f(b)-f(a) b-a =f'(c) 证明:构造辅助函数 Tangent parallel to chord F(x)-f(b)-f(@x-f(x) b-a Slopef"(c) B 直接应用Rolle定理 Slope fb)-f(a) b-a y X a b y=f(x)
Lagrange中值定理 [ , ] ( , ) ( , ), ( ) ( ) ( ) f a b a b c a b f b f a f c b a 若函数 在 上连续,在 内可导,则 ( ) ( ) ( ) ( Roll ) , e f b f a F x x f x b a 证明:构造辅助函数 直接应用 定理