数项级数
数项级数

例: 2.317=2.3171717… =2.3+17+1717 +… 103105107 1147 1 495 100 ++4++5 9 π=3 10100100010000100000
例: 3 5 7 3 3 0 2.317 2.3171717 17 17 17 2.3 10 10 10 17 1 17 1 1147 2.3 2.3 . 10 100 10 495 1 1 100 1 4 1 5 9 3 10 100 1000 10000 100000 n n
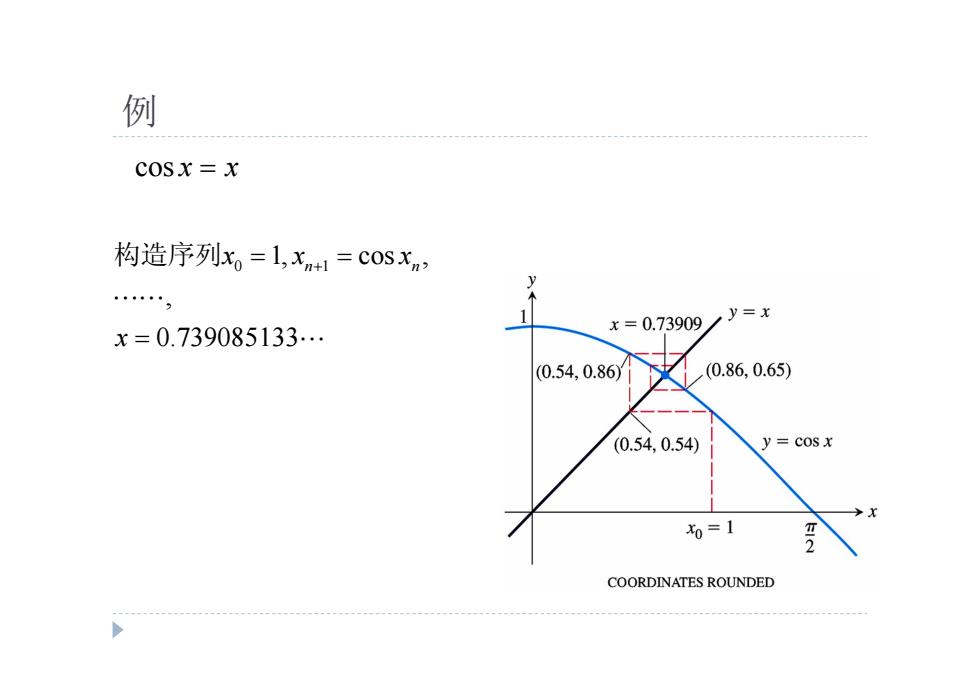
例 COSX=X 构造序列x,=1,xn+1=COS, x=0.739085133.… x=0.73909/y=x (0.54,0.86) (0.86,0.65) (0.54,0.54) y=cosx x0=1 2 COORDINATES ROUNDED
例 cos x x 0 1 1, cos , , 0.739085133 n n x x x x 构造序列

常数项级数 常数项级数:∑a,=a,+a,+a,+… k=] 常数项级数部分和:Sn=a4+a2+…+an= S=lim S,=lim∑a称为级数的和,如果部分和序列{Sn}收敛,称 k=1 级数∑a,收敛(series converges,)否则称级数∑a,发散(series diverges) k=1 k=1
常数项级数 1 2 3 1 k k a a a a 常数项级数: 1 2 1 n n k n k S a a a a 常数项级数部分和: 1 1 1 lim lim (series converges) (series diverges) n n k n n n k k k k k S S a S a a 称为级数的和,如果部分和序列 收敛,称 级数 收敛 ,否则称级数 发散

例:等比级数(惐几何级数,geometric series)) 12ag=a+ag+ag+,a≠0 k=0 a-ag" 解:Sn=a+ag+ag+…+ag= 9≠1 {1-q na, 9=1
例:等比级数 (或几何级数,geometric series) 2 0 1 , 0 k k aq a aq aq a 、 2 1 , 1 1 , 1 n n n a aq q S a aq aq aq q na q 解:

例 m=1 名 =1 53=34 十5=23 数 1有 -s1=1/2 应
例 1 1 k k k 1 1 1 k k 发散 1

收敛级数的运算和性质 如果级数2a6都收敛,则级数2(a,+Bb,)地收敛,且 k= 三(a,+B)片u2a+p4 k=] 收敛级数∑a加括号后所成的级数依然收敛,且与原级数有 相同的和
收敛级数的运算和性质 1 1 1 1 1 1 + + = + k k k k k k k k k k k k k k a b a b a b a b 如果级数 、 都收敛,则级数 也收敛,且 1 k k a 收敛级数 加括号后所成的级数依然收敛,且与原级数有 相同的和

例 到 会2日 *2号+ 1111.1.1 3、1+ 2244t4+4++ 2” 2 2
例 1 5 1 1 ( 1) 2n n n n 、 1 1 1 1 5 1 1 1 1 + =5 + =6 ( 1) 2 1 2 n n n n n n n n n n 2 1 1 2 2 3 n n n n 、 1 1 1 2 5 1 9 3 3 12 n n n n n n 2 4 2 1 1 1 1 1 1 1 1 1 3 1 2 2 4 4 4 4 2 2 2 n n n n

发散级数的一个判别法 如果级数∑a,收敛,那么ima:=0 k-o0 k=1 1∑n发散,因n2→0 =】 2∑(-1发散
发散级数的一个判别法 2 2 1 1 n n n 、 发散,因 1 1 2 ( 1)n n 、 发散 1 1 1 3 1 n n n n n 、 发散,因 1 4 n 2 5 n n 、 发散 1 lim 0 k k k k a a 如果级数 收敛,那么

收敛级数添加或取消项 在级数∑a,前面去掉或加上有限项,不影响级数的敛散性 k=1 1=111 日5”5251253
收敛级数添加或取消项 1 k k a 在级数 前面去掉或加上有限项,不影响级数的敛散性 1 4 1 1 1 5 25 125 1 1 5 5 n n n n