北京化工大学：《微积分》课程授课教案（专题讲稿）工科数学分析专题——函数项级数

函数项级数

函数项级数

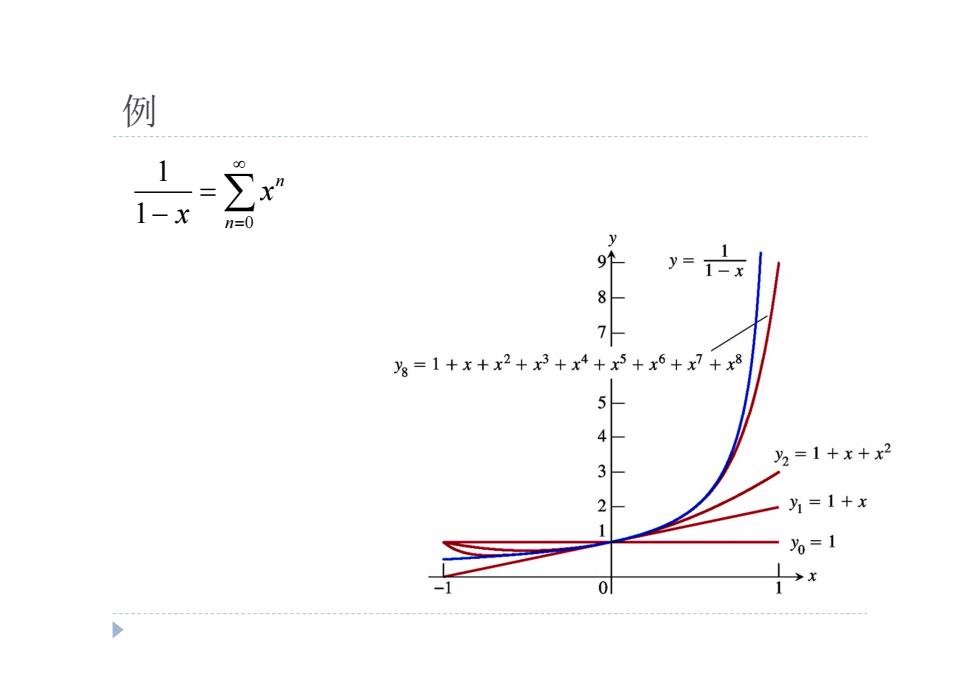
例 =1+x+x2+x3+x4+x+x6+x7 5 2=1+x+x2 2 为=1+x %=1 0 1x

例 0 1 1 n n x x     

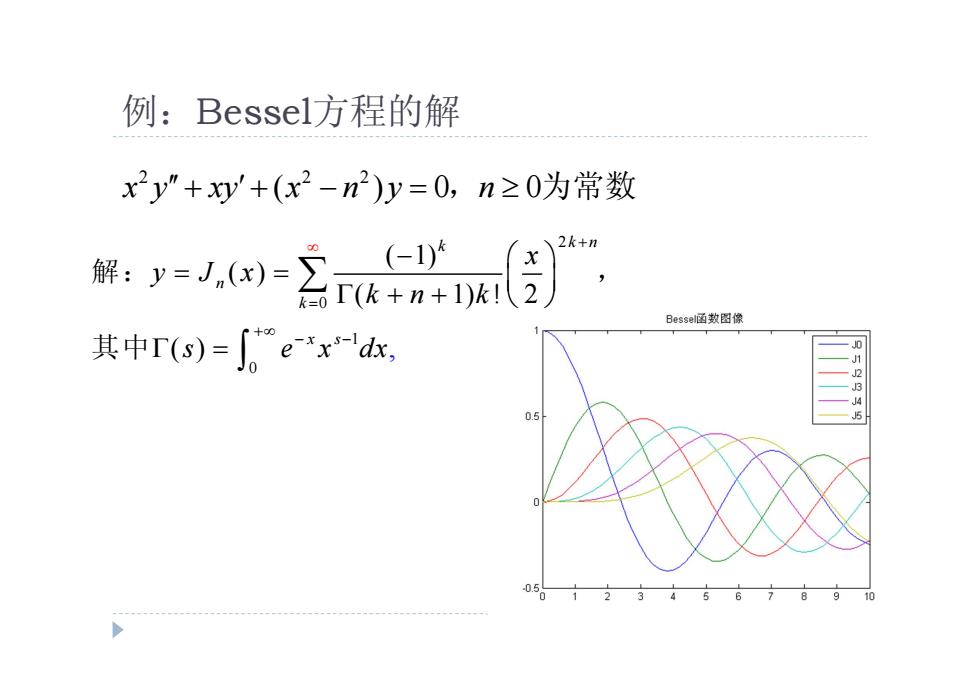
例：Bessel方程的解 x2y"+y'+(x2-n2)y=0,n≥0为常数 :y-1w-24g 2k+n Bessel函数图像 其中T(s)=∫0e*xd, 0.5 J5 0.5 6789 10

例：Bessel方程的解 2 2 2 x y xy x n y n        ( ) 0 0 ， 为常数 2 0 1 0 ( 1) ( ) ( 1) ! , 2 ( ) k n k n k x s x y J x k n k s e x dx                       解： ， 其中

函数项级数 设{u,(x)}是定义在集合DcR上的一列函数（称为函数列），则 立，()=4(+L()++u()+称为笑合D上的函数项级数 部分和S,=24,(x) k=1 若对某个∈D,∑4，(3)收敛，则称x是∑，(x)的收敛点，否则称为发散点： 由收敛点的全体所构成的集合称为∑，(x)的收敛域，所有发散的点的全 =1 体称为发散域。若x∈D,∑，(x)都收敛，则称该级数在D上逐点收敛

函数项级数   1 2 1 ( ) ( ) ( ) ( ) ( ) n n n n u x D u x u x u x u x D             设 是定义在集合 上的一列函数（称为函数列），则 称为集合 上的函数项级数 0 0 0 1 1 , ( ) ( ) n n n n x D u x x u x     若对某个    收敛，则称 是 的收敛点，否则称为发散点； 1 ( ) n n k k S u x  部分和   1 1 ( ) , ( ) n n n n u x x D u x D         由收敛点的全体所构成的集合称为 的 ，所有发散的点的全 体称为发散域。若 都收敛，则 收敛 称该级数在 上 域 逐点收敛

例 判少 1的收敛域 n=1 1+x 解 4+(x） (n→0) lu(x n+11+x1+x 0当 + 1,即x>0或x1→+k1,即-2<x<0时，原级数发散 (3)当11+x卡1，→x=0或x=-2,当x=0时，级数1少收敛 =1 n 当x=2时，级数∑发散，故级数的收敛域为（∞，-2）U[0,+∞)

例 1 ( 1) 1 ( ) 1 n n n n x     判断 的收敛域     1 1 1 1 1 ( ) 1 1 1 1 (1) 1, 1 1, 0 2 , 1 1 (2) 1, 1 1, 2 0 ( ) ( , 1 ( 1) (3) |1 | 1, 0 2 ) , 2 0 0 1 , , , 2 , n n n n n n n n x x x x x x x x x x u x x x x n u x n x                                              解： 当 即 或 时 原级数绝对收敛 当 即 时 原级数发散 当 或 当 时 级数 收敛 当 时 级数 发散，故级数的收敛域为

例 研究级数x+(x2-x)+(x3-x2)+…+(x”-x-)+…的收敛性 解：S(x)=limS(x)=limx” x1时，Sn(x)=x”→∞ 故该级数的收敛域为(-1,0]，发散域为(-o,-]U(1,+∞)

例 2 3 2 1 ( ) ( ) ( ) n n x x x x x x x  研究级数          的收敛性 0, 1, ( ) lim ( ) lim 1, 1. 1 ( 1) ( 1) , 1 ( ) ( 1 0] ( , 1] (1, ) n n n n n n n n x S x S x x x x S x S x x                         解: 当 时， 当 时， 故该级数的收敛域为 ，，发散域为

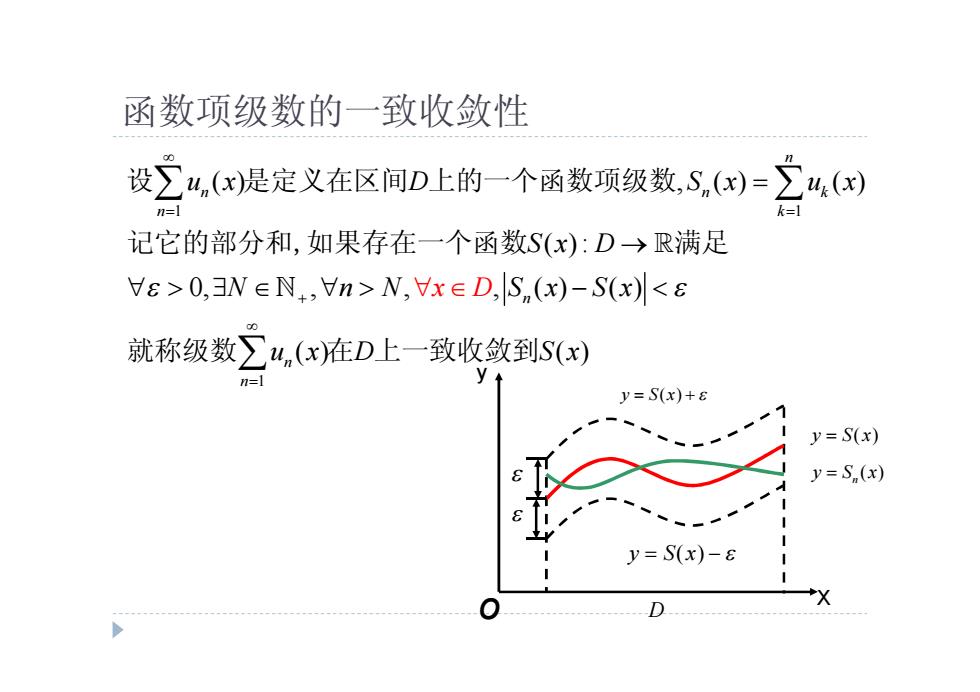
函数项级数的一致收敛性 设2，(x是定义在区间D上的一个函数项级数，S,()=4,() k=1 记它的部分和，如果存在一个函数S(x):D→R满足 Vs>0,3N∈N,n>N,Vx∈D,Sn(x)-S(x)<& 就称级数∑4，(x)在D上一致收敛到S(x) n=1 y=S(x)+8 27 y=S(x) y=S,(x) y=S(x)-ε

函数项级数的一致收敛性 X y o D y S x   ( )  y S x   ( )  y S x  ( ) ( ) n  y S x   1 1 1 ( ) , ( ) ( ) ( ) : 0, , , , ( ) ( ) ( ) ( ) n n n k n k n n n u x D S x u x S x D N n N S x S x x u x D S D x                          设 是定义在区间 上的一个函数项级数 记它的部分和,如果存在一个函数 满足 就称级数 在 上一致收敛到

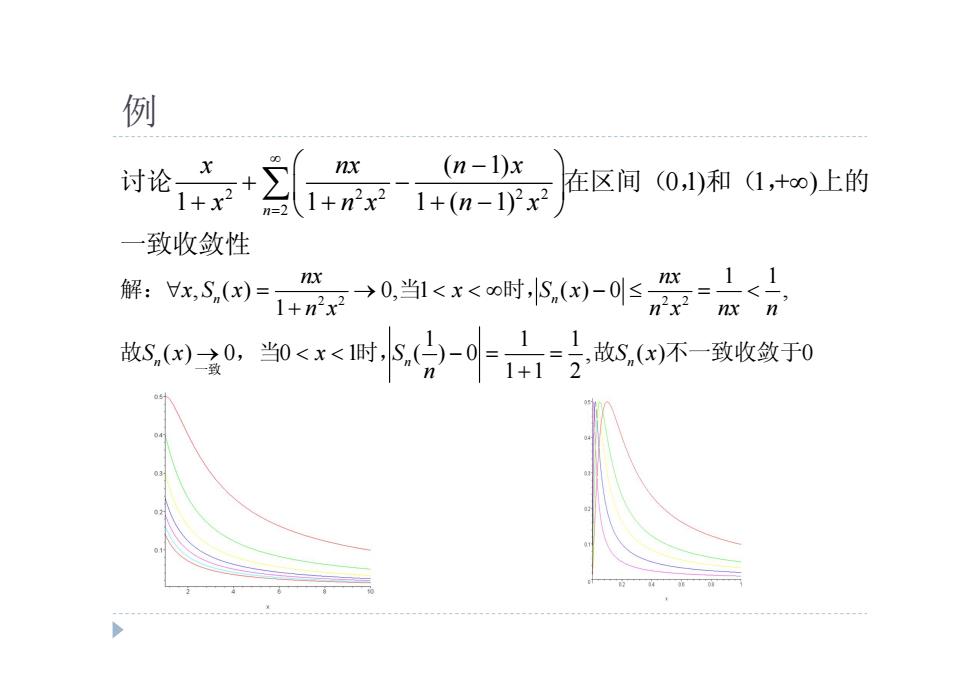
例 (n-1)x 1+(n-1)2x2 在区间(0,1)和(1，+0)上的 一致收敛性 解，x5(国1价→0当1时-器 n'x2nx n 放国子0，当0<时-古-分故（怀-致收敛于和

例 2 2 2 2 2 2 ( 1) 0 1) 1 + ) 1 1 1 ( 1) n x nx n x x n x n x                 讨论  在区间（ ，和（ ， 上的 一致收敛性 2 2 2 2 1 1 , ( ) 0, 1 ( ) 0 , 1 1 1 1 ( ) 0 0 1 ( ) 0 , ( ) 0 1 1 2 n n n n n nx nx x S x x S x n x n x nx n S x x S S x n                  一致  解： 当 时， 故 ，当 时， 故 不一致收敛于

Cauchy收敛原理 定义在D上的级数∑u,(x)一致收敛的充要条件是 n=】 s0 Vat.Vp.pcK.当nv三aae 证明：必要性：Sn+p(x)-S,(x)≤Sn+p(x)-S(x)+Sn(x)-S(x 充分性：由数列Cauchy!收敛原理，对任意固定的x∈D,部分和序列 S(收敛，设其极限函数为s在斗，()-S(训-三4（✉中令 p→o,立即得到一致收敛性

Cauchy收敛原理 1 1 ( ) 0, , , , ( ) n n n p k k n D u x   N n p n N x D u x                      定义在 上的级数 一致收敛的充要条件是 ，当 时 ， 1 ( ) ( ) ( ) ( ) ( ) ( ) Cauchy ( ) ( ), ( ) ( ) ( ) , n p n n p n n p n n p n k k n S x S x S x S x S x S x x D S x S x S x S x u x p                  证明：必要性： 充分性：由数列 收敛原理，对任意固定的 ，部分和序列 收敛，设其极限函数为 在 中令 立即得到一致收敛性

一 致收敛的Weierstrass判别准则 级数∑4，(x)定义在D上，如果存在收敛的正项级数∑Mn,满足 n- n= 4,(x≤Mnn=1,2,…,x∈D,那么级数∑，(x)在D上一致收敛 证明：4n1(x)+4H2()+…+4+p(x) ≤un(+un2(x+…+n+p()≤Mnl+Mn2++Mnp<E

一致收敛的Weierstrass判别准则 1 1 1 ( ) , ( ) 1,2, , ( ) n n n n n n n n u x D M u x M n x D u x D               级数 定义在 上，如果存在收敛的正项级数 满足 ， ，那么级数 在 上一致收敛 1 2 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) , n n n p n n n p n n n p u x u x u x u x u x u x M M M                          证明：