多重积分
多重积分
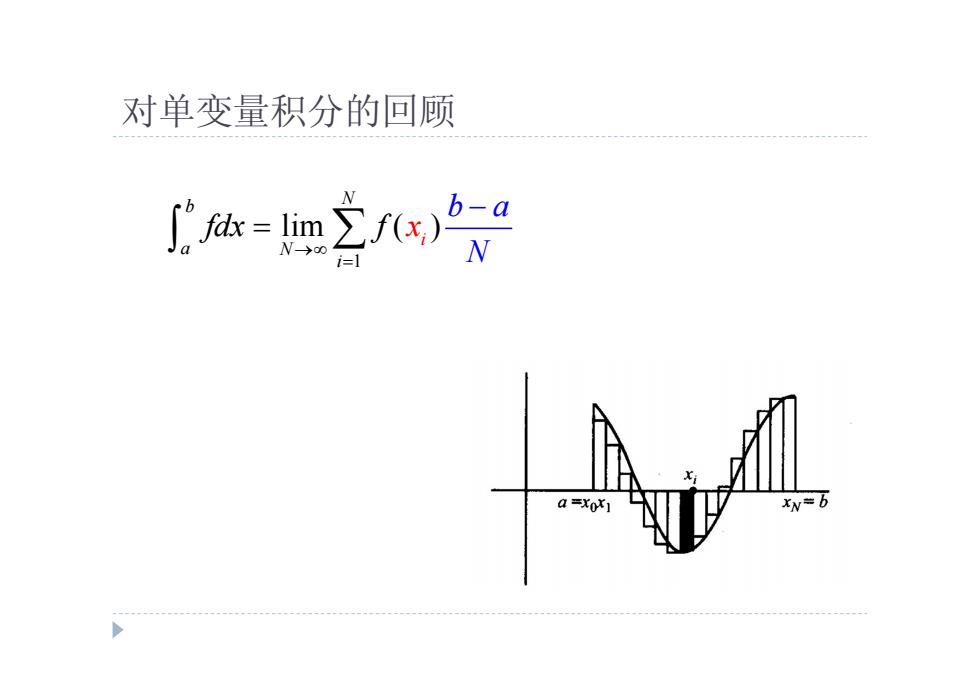
对单变量积分的回顾 g体=e2)2 N>oo i-1 a=x0
对单变量积分的回顾 1 lim ( ) N b a i N i fdx f b a N x

矩形区域上的分割 I=[a,b]×[c,d]是R中的闭矩形,作a,b的分割△x:a=。<x1<…<xn=b, 又作[c,d]的分割△:c=<<…<ym=d,两族平行线:x=x,与y=y =0,1,,n,j=0,1,…,m),把I分割成k=n×m个子矩形x-,x]x[y-×y, (i=0,L,…n,j=0,l,…,m),这k个子矩形全体组成的一个分割△=△×△, 用一定的次序重排这k个子矩形,将它们编号为1,2,…,I,在每一个,中 任取一点,i=l,2,k,作积分和(也称Riemann和)∑f(5)o(),其中 o(L)=(b-a)×(d-c),记△=max{diam(I),…,diam(Ix)},diam(I,)是矩形 I的对角线长度,称之为分割△的宽度
矩形区域上的分割 2 0 1 0 1 1 1 [ , ] [ , ] [ , ] : [ , ] : ( 0,1, , , 0,1, , ), , ( 0,1,, , 0,1, ] , [ ] [ ) , i i j x n y m i j j x y x x y I a b c d R a b a x x x b c d c y y y d x x y y i n j m I k n m m k y i n j I 是 中的闭矩形,作 的分割 , 又作 的分割 ,两族平行线: 与 , 把 分割成 个子矩形: ,这 个子矩形全体组成 的一个分割 , 用一定的 1 2 1 = max diam( ), ,di 1 , , , , 1 2 , Riemann , , ,diam( am( ) ) k i i i i i i i i k k f I I k I I I I i k I b a d c I I I 次序重排这 个子矩形,将它们编号为 在每一个 中 任取一点 , , , 作积分和(也称 和) 其中 记 是矩形 的对角线长度,称之为分割 的宽度

矩形区域上二重积分的定义 如果存在数4使得对Hε>0,36>0,V满足△<δ的分割,V5,∈I,都有 立f(5)o(U)-A<6便称函数在矩形1上可积,并将泻作 f(x,y)d域jf(x)dk
矩形区域上二重积分的定义 1 0, 0, , ( , ) i i k i i i I I A I f I A f I A f x y dxdy f d x x 如果存在数 使得对 满足 的分割, 都有 便称函数 在矩形 上可积,并将 写作 或
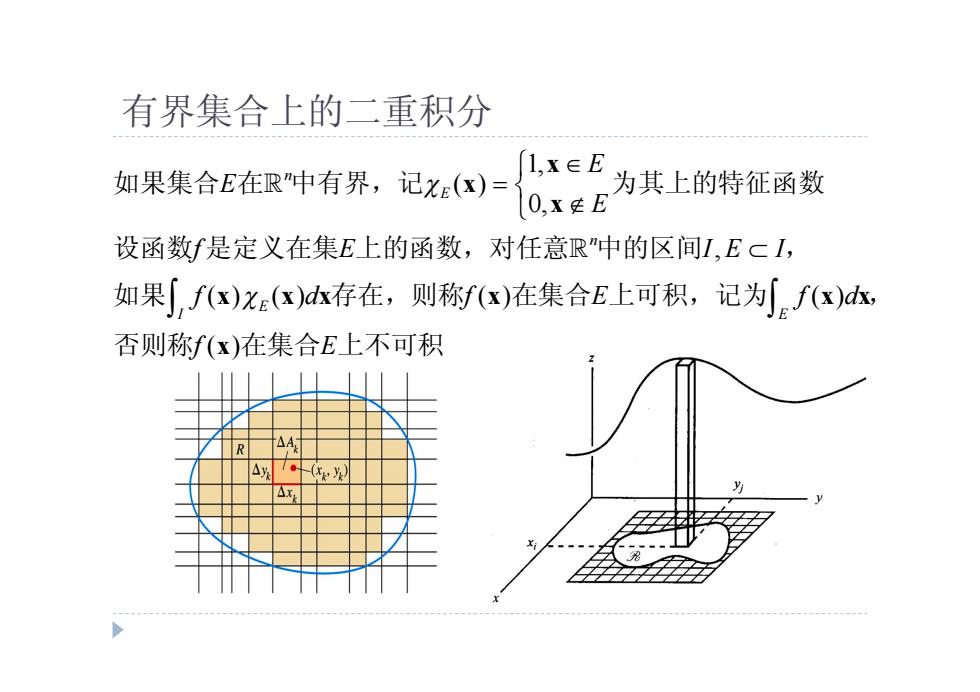
有界集合上的二重积分 如果集合E在R中有界,记X(x)= 1,x∈E 为其上的特征函数 0,xE 设函数f是定义在集E上的函数,对任意R"中的区间L,EcI, 如果,f(x)x(x)k存在,则称f(x)在集合E上可积,记为f(x)k, 否则称f(x)在集合E上不可积 R Ax
有界集合上的二重积分 1, ( ) 0, , ( ) ( ) ( ) ( ) ( ) n E n E I E E E E f E I E I f d f E f d f E x x x x x x x x x x 如果集合 在 中有界,记 为其上的特征函数 设函数 是定义在集 上的函数,对任意 中的区间 , 如果 存在,则称 在集合 上可积,记为 , 否则称 在集合 上不可积
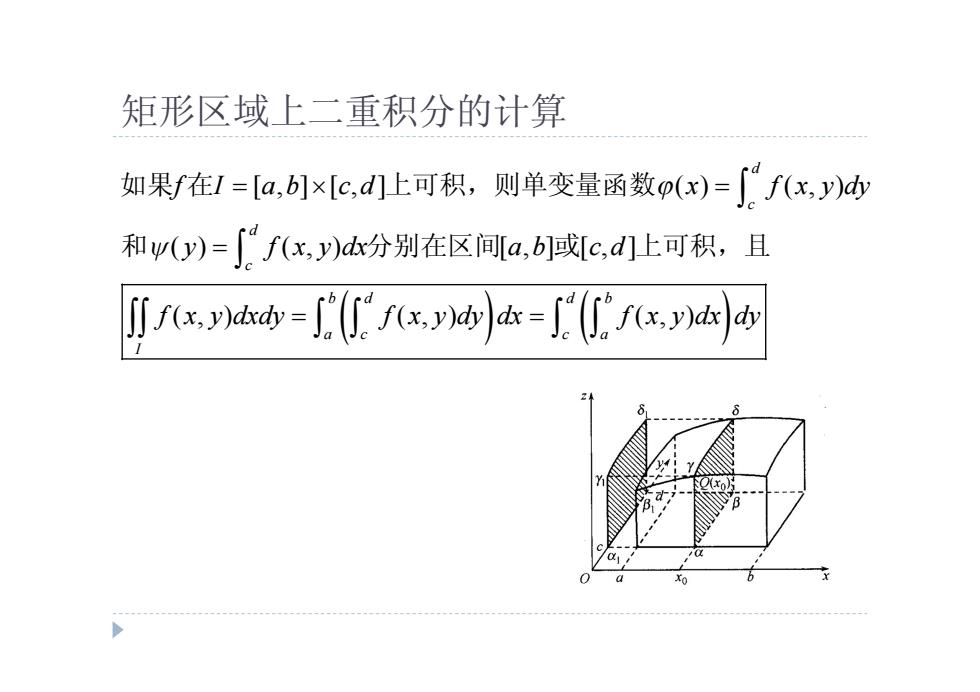
矩形区域上二重积分的计算 如果f在I=[a,b]x[c,d]上可积,则单变量函数p(x)=∫f(x,)山 和yw(y)=∫f(x,y)d分别在区间[a,b]或[c,d上可积,且 ∬fx,dk=(fxy=fx,d
矩形区域上二重积分的计算 [ , ] [ , ] ( ) ( , ) ( ) ( , ) [ , ] [ , ] ( , ) ( , ) ( , ) d c d c b d d b a c c a I f I a b c d x f x y dy y f x y dx a b c d f x y dxdy f x y dy dx f x y dx dy 如果 在 上可积,则单变量函数 和 分别在区间 或 上可积,且
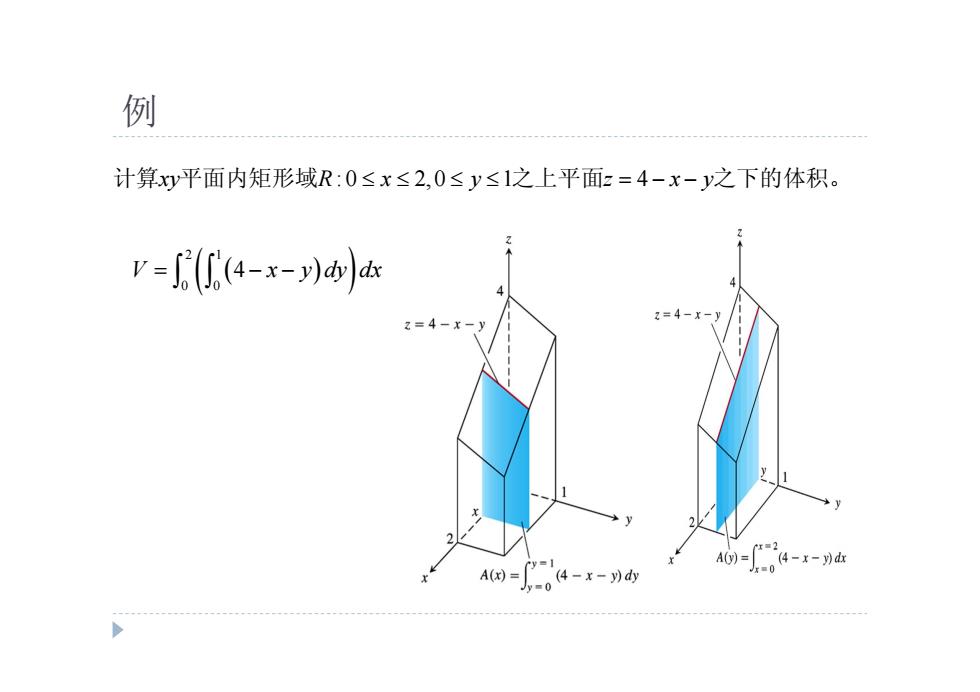
例 计算y平面内矩形域R:0≤x≤2,0≤y≤1之上平面z=4-x-y之下的体积。 r=4-x-列 =4-x A(x)= -04-x-yd西
例 计算xy R x y z x y 平面内矩形域 : 0 2,0 1 4 之上平面 之下的体积。 2 1 0 0 V x y dy dx 4

例 J,ysin(xy)d,I=[0,π]×[0, 0.0 =(ysin()4
例 sin , [0, ] [0,1] I y xy dxdy I 1 0 0 sin 1 y xy dx dy
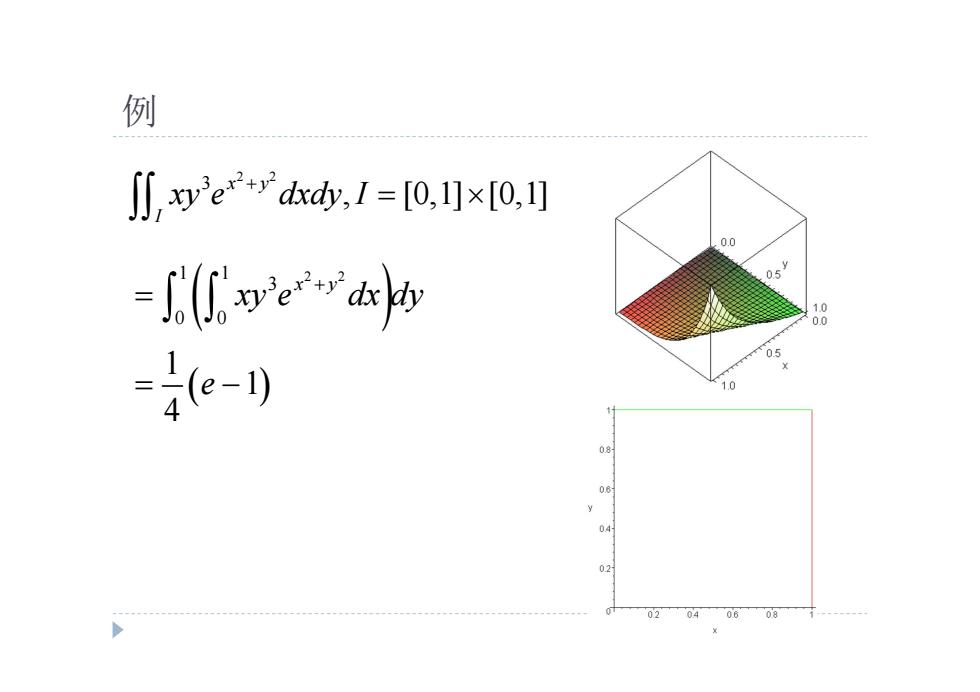
例 J∬,9yerd,1=0,1×f0,1] 0.0 -jyer 05 0.5 =4e-0 0 04 02 09 06 08
例 2 2 3 , [0,1] [0,1] x y I xy e dxdy I 1 1 2 2 3 0 0 1 1 4 x y xy e dx dy e
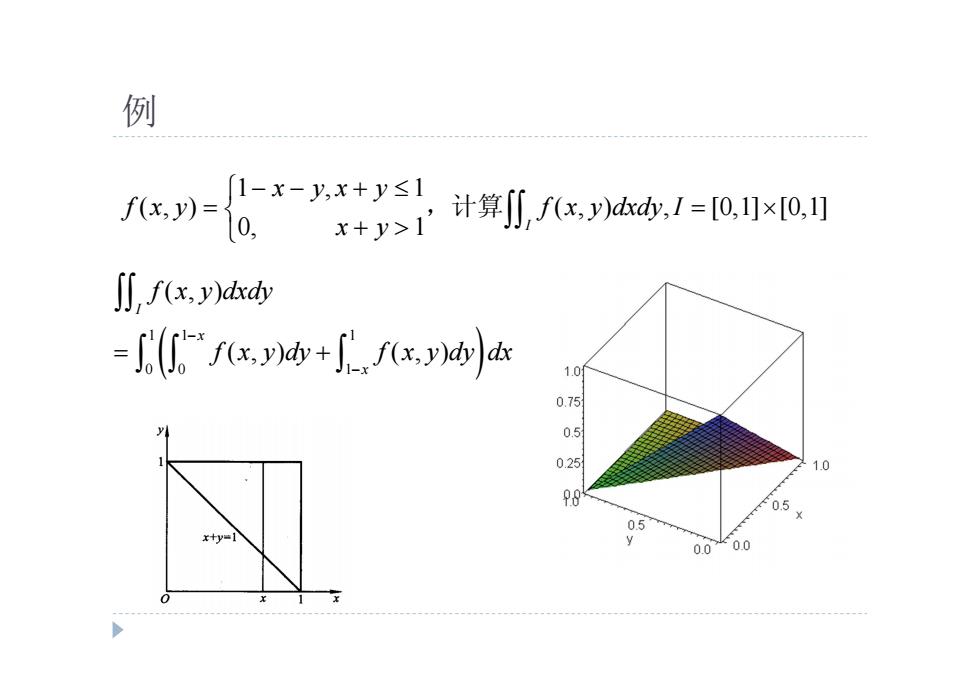
例 f(x,y)= 1-x-y,x+y≤1 0, x+y>1 计算,fx,I=ox0, ∬fx,y)d .ds 10 015 0.5 0.25 10 98 05¥ 05 xty=1 0.0 k0.0
例 1 , 1 ( , ) ( , ) , [0,1] [0,1] 0, 1 I x y x y f x y f x y dxdy I x y ,计算 1 1 1 0 0 1 ( , ) ( , ) ( , ) I x x f x y dxdy f x y dy f x y dy dx