北京化工大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵 第二节 矩阵的运算

第二节矩阵的运算 矩阵加法 二 数乘矩阵 三矩阵乘法 四 典型例题 五、小结 思考题 D

第二节 矩阵的运算 一 矩阵加法 二 数乘矩阵 三 矩阵乘法 四 典型例题 五、小结 思考题

一、矩阵的加法 1、定义 设有两个m×n矩阵A=(a,)B=(b,)那末矩阵 A与B的和记作A+B,规定为 (a1+b1 a2+b2 4+B= a21+b12n+b2 …a2n+b2n 上页 这回

１、定义               + + + + + + + + + + = m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 一、矩阵的加法 设有两个 矩阵 那末矩阵 与 的和记作 ，规定为 mn A (a ), B (b ), = ij = ij A B A+ B

说明只有当两个矩阵是同型矩阵时，才能进 行加法运算. 12 3 -5 18 9 例如 1 -9 0 + 6 5 4 3 6 8 3 21 12+1 3+8 -5+9 13 11 4 1+6 -9+5 0+4 7 -4 4 3+3 6+2 8+1 6 8 上页

说明 只有当两个矩阵是同型矩阵时，才能进 行加法运算. 例如           +           − − 3 2 1 6 5 4 1 8 9 3 6 8 1 9 0 12 3 5           + + + + − + + + + − + = 3 3 6 2 8 1 1 6 9 5 0 4 12 1 3 8 5 9 . 6 8 9 7 4 4 13 11 4           = −

2、 矩阵加法的运算规律 ()A+B=B+A; (2)(A+B)+C=A+(B+C) -l12 (3)-A= -22 -2 一mi 称为矩阵A的负矩阵 4)A+(-A)=0,A-B=A+（-B) 区回

2、 矩阵加法的运算规律 (1) A+ B = B + A; (2)(A+ B)+ C = A+ (B + C). ( )               − − − − − − − − − − = m m m n n n a a a a a a a a a A        1 1 21 22 2 11 12 1 3 (4) A+ (− A) = 0, A− B = A+ (− B). ( ), = − aij 称为矩阵A的负矩阵

二、数与矩阵相乘 1、定义 数2与矩阵4的乘积记作4或A几，规定为 211 212 2A=A入= 221 222 22n … Aam Aam … Mmn

1、定义 . 1 1 2 1 2 2 2 1 1 1 2 1               = = m m mn n n a a a a a a a a a A A                   二、数与矩阵相乘 数与矩阵A的乘积记作A或A,规定为

2、数乘矩阵的运算规律 (设A、B为mxn矩阵，2，u为数) ()(a4)A=2(4 (2)+P)A=M+4 (3)(A+B)=24+B. (4)1A=A 矩阵相加与数乘矩阵合起来，统称为矩阵的线 性运算。 回

(1)()A = (A); (2)( + )A = A+ A; ( ) ( ) A A A B A B = + = + (4)1 3    . 2、数乘矩阵的运算规律 矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算. （设 A、B 为 mn 矩阵，  , 为数）

三、矩阵与矩阵相乘 问题的引入：学院进行体育比赛，四个年级分别获得金、银、 铜牌数为：四年级：3、3、1，三年级：5、4、2，二年级： 4、5、6,一年级：4、4、7； 规定金牌(3分，500元)、银牌(2分，300元)、铜牌(1 100元) 试设计一个表格，及一种运算计算每个年级：总分数，总奖 金数

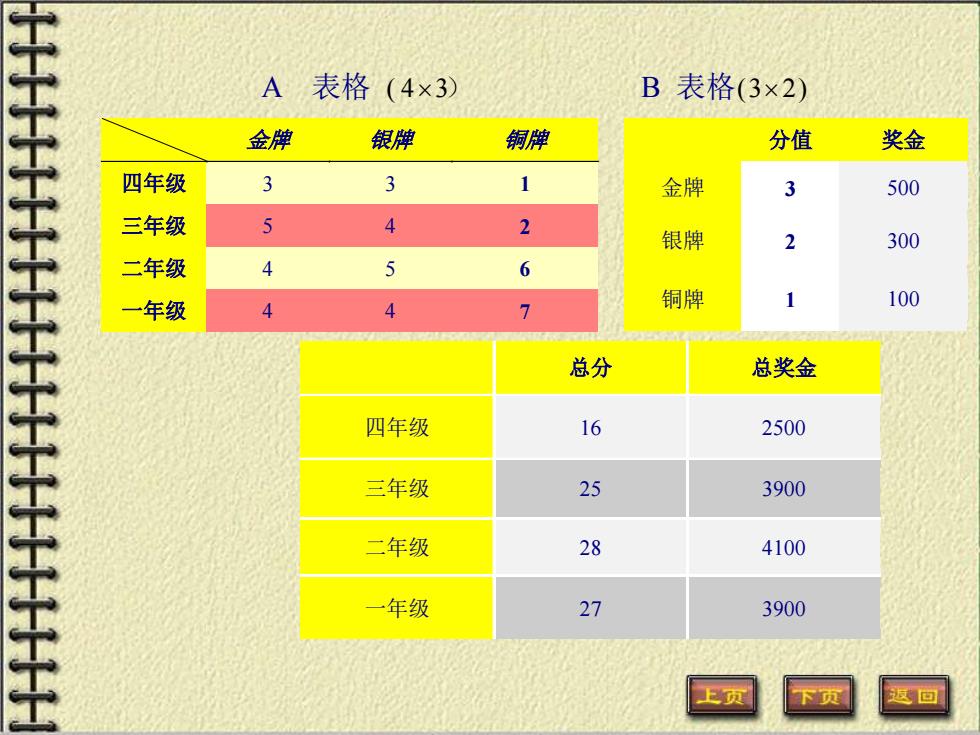
问题的引入：学院进行体育比赛，四个年级分别获得金、银、 铜牌数为：四年级：3、3、1，三年级：5、4、2，二年级： 4、5、6，一年级：4、4、7； 规定 金牌（3 分，500 元）、银牌（2 分，300 元）、铜牌（1 分， 100 元） 试设计一个表格，及一种运算计算每个年级：总分数，总奖 金数。 三、矩阵与矩阵相乘

A表格(4x3) B表格(3×2) 金牌 银牌 铜牌 分值 奖金 四年级 3 3 1 金牌 3 500 三年级 5 4 2 银牌 2 300 二年级 4 5 6 一年级 1 4 4 7 铜牌 100 总分 总奖金 四年级 16 2500 三年级 25 3900 二年级 28 4100 年级 27 3900 上页 区回

A 表格 ( 43） B 表格(3 2) 金牌 银牌 铜牌 四年级 3 3 1 三年级 5 4 2 二年级 4 5 6 一年级 4 4 7 分值 奖金 金牌 3 500 银牌 2 300 铜牌 1 100 总分 总奖金 四年级 16 2500 三年级 25 3900 二年级 28 4100 一年级 27 3900

条件AB,-C左边矩阵的列数等于右边矩阵的行数 例考虑矩阵 4143 468 B=0 -13 1 275 2 A是一个2×3矩阵，B是一个3×4矩阵，乘积4B 是一个2×4矩阵，用表格来演示乘法： 上页

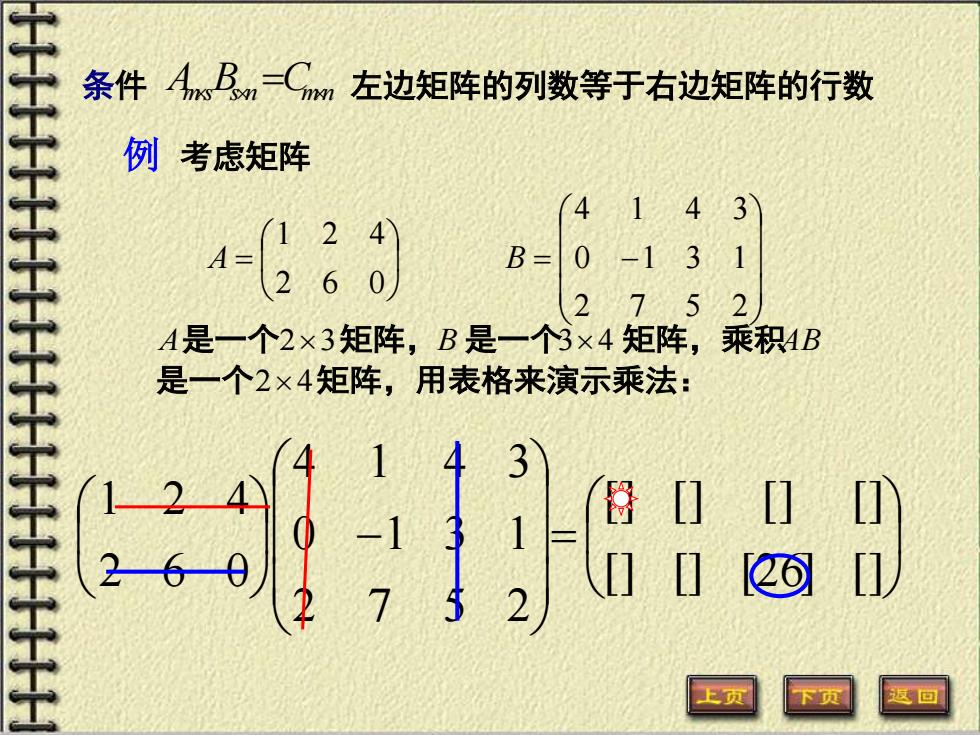
条件 AmsBsn =Cmn 左边矩阵的列数等于右边矩阵的行数 例 考虑矩阵       = 2 6 0 1 2 4 A           = − 2 7 5 2 0 1 3 1 4 1 4 3 B A是一个23矩阵，B 是一个34 矩阵，乘积AB 是一个24矩阵，用表格来演示乘法：       =            −      [] [] [26] [] [] [] [] [] 2 7 5 2 0 1 3 1 4 1 4 3 2 6 0 1 2 4

(24)+(63)+(05)=26 4B- 27 30 13 2612 A B AB mx Fr xn m xn 上页 这回

(24)+(63)+(05) =26       − = 8 4 26 12 12 27 30 13 AB m n AB m r r n A B  =  