
第六节利用初等变换求逆矩阵 定义18n阶单位阵经过一次初等变换所 得到的矩阵,称为初等矩阵,简称初等 阵。 三种初等变换对应了三种初等阵 (1)换法初等阵交换E的1两行(列) 得到的方阵,记为E”即 这回
第六节 利用初等变换求逆矩阵 定义18 n阶单位阵经过一次初等变换所 得到的矩阵,称为初等矩阵,简称初等 阵。 三种初等变换对应了三种初等阵 得到的方阵,记为 ,即 换法初等阵 交换 的 两行(列) E(i, j) (1) E i, j
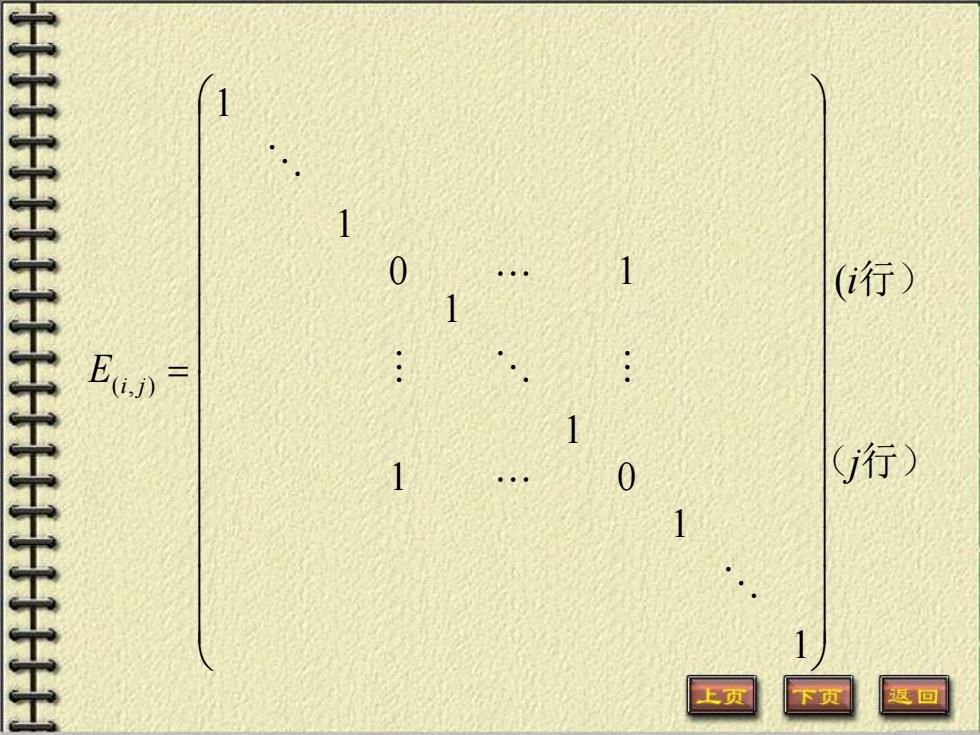
1 1 (i行) 1 : 1 0 行)
( 行) 行) j i E i j ( 1 1 1 0 1 1 0 1 1 1 ( , ) =
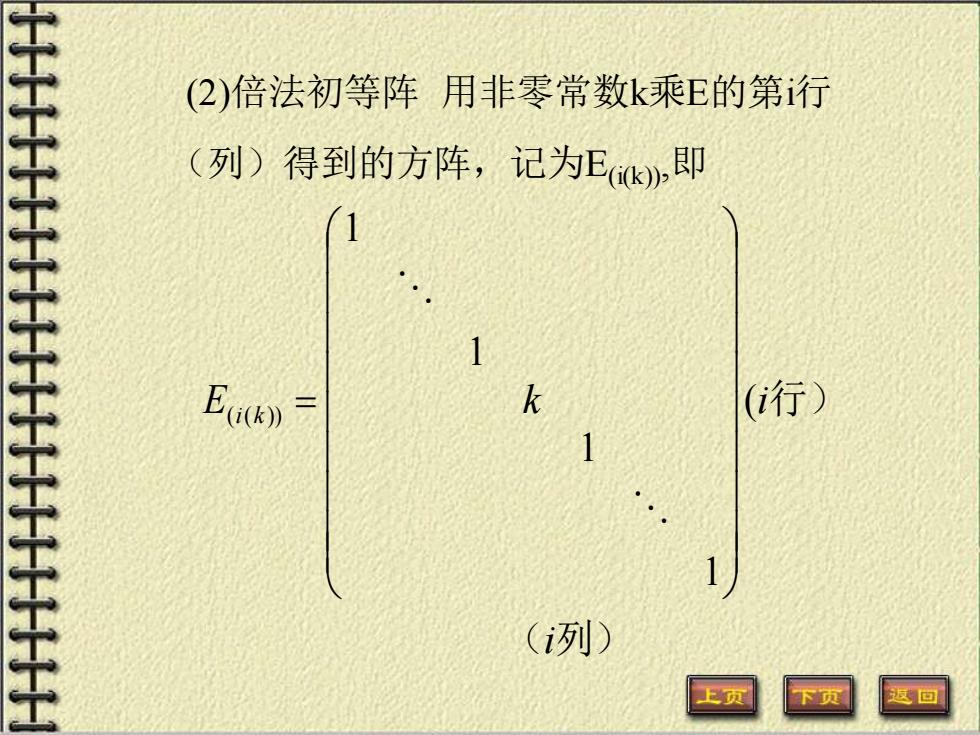
(2)倍法初等阵用非零常数k乘E的第行 (列)得到的方阵,记为E,即 1 1 (行) 1 1 (列) 上页 下页 返回
(2)倍法初等阵 用非零常数k乘E的第i行 (列)得到的方阵,记为E(i(k)),即 ( 列) 行) i E k i i k ( 1 1 1 1 ( ( )) =
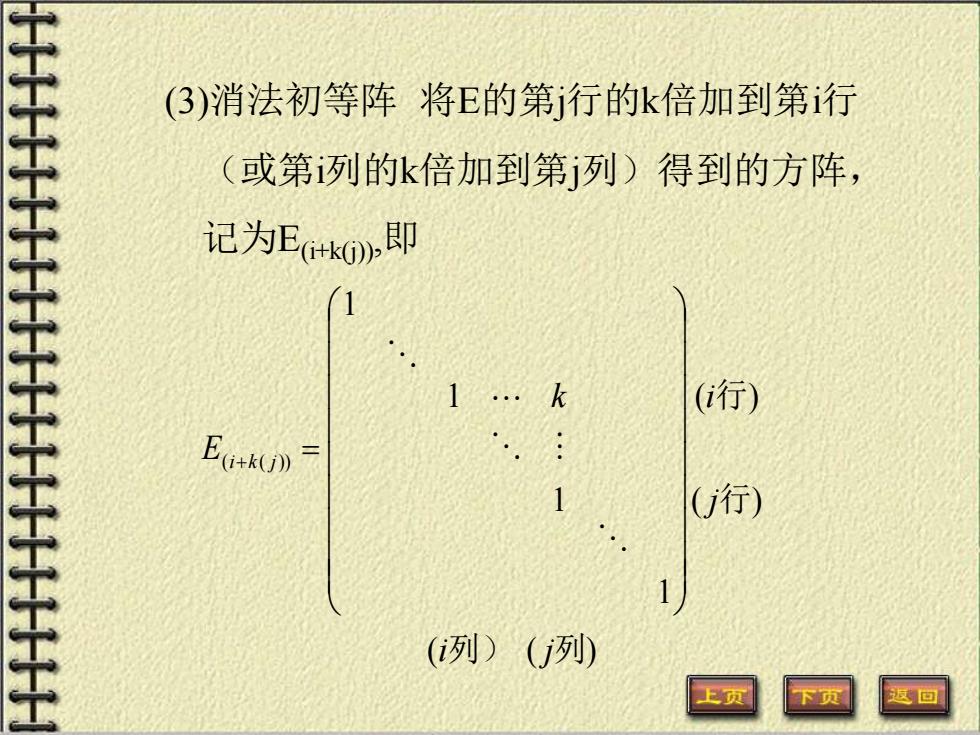
(3)消法初等阵将E的第j行的k倍加到第行 (或第列的k倍加到第j列)得到的方阵, 记为E+kO,即 1 1..k (行) EG+U》 1 (行) (列)(列)
(3)消法初等阵 将E的第j行的k倍加到第i行 (或第i列的k倍加到第j列)得到的方阵, 记为E(i+k(j)),即 ( ( ) ( ) ( ) 1 1 1 1 ( ( )) 列) 列 行 行 i j j k i E i k j + =

初等矩阵具有下列性质 (1)初等矩阵都是可逆阵,且它们的逆阵 仍为同类初等阵,即 Bd-Ra B-bs-m (2)对m×n矩阵A作一次初等行变换,相 当于在A的左边乘上一个m阶相应的初等阵; 对m×n矩阵A作一次初等列变换,相当于在 A的右边乘上一个n阶相应的初等阵。 这回
初等矩阵具有下列性质 (1)初等矩阵都是可逆阵,且它们的逆阵 仍为同类初等阵,即 ( , ) 1 E(i, j) = E i j − )) 1 ( ( 1 ( ( )) k i E i k = E − ( ( )( )) 1 E(i k ( j)) E i+ −k j − + = (2)对m×n矩阵A作一次初等行变换,相 当于在A的左边乘上一个m阶相应的初等阵; 对m×n矩阵A作一次初等列变换,相当于在 A的右边乘上一个n阶相应的初等阵

证明:仅证行变换的情况。 将m×n阵A=(a,)按行分成 a11 412 A a21 022 … A= A2n am am2 上页
仅证行变换的情况。 = Am A A 2 1 = m m mn n n a a a a a a a a a A 1 2 21 22 2 11 12 1 将mn阵A = (ai j)按行分成 证明:

4: 4:. 0 1 Ed4= 1 0 4 上页 这回
1 1 ( , ) 1 1 0 0 1 1 = m m j i m m i j A A A A E A 1 1 = m m i j A A A A

主王二二二二二二二二王王 1 A E(k4 k . kA 1 mxm mx mx 上页 下 回
1 1 ( ( )) 1 1 = m m i m m i k A A A E A k 1 1 = m m i A kA A

1 4三 1 A +kA Eu+kU》A= 1 4:. mxl 王页 返回
1 1 ( ( )) 1 1 1 1 + = m m j i m m i k j A A A A k E A 1 1 + = m m j i j A A A kA A

定理3任一m×n矩阵A,一定存在有限 个m阶初等阵P,P,…,P,和n阶初等阵Q1, Q2,…,0,使 Bgg-58-1 推论1如果n阶方阵A可逆,一定存在有 限个n阶初等阵P,P2,…,P;Q1,Q2,…,2, 使 P…PAQ…Q,=E 上页
使 个 阶初等阵 和 阶初等阵 任一 矩阵 ,一定存在有限 , , , m , , , n Q , A 2 1 2 1 t s Q Q P P P m n I E P P AQ Q r s t = = 0 0 0 1 1 P P AQ Q E P P P Q Q n s t s t = 1 1 1 2 1 2 n , , , ;Q , , , , A 使 限个 阶初等阵 如果 阶方阵 可逆,一定存在有 定理3 推论1