北京化工大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵 第三节 特殊矩阵

第三节 特殊矩阵 单位方阵 一二三四五六 对角阵 三角阵 转置矩阵 对称矩阵 奇异方阵

第三节 特殊矩阵 一 单位方阵 二 对角阵 三 三角阵 四 转置矩阵. 五 对称矩阵 六 奇异方阵

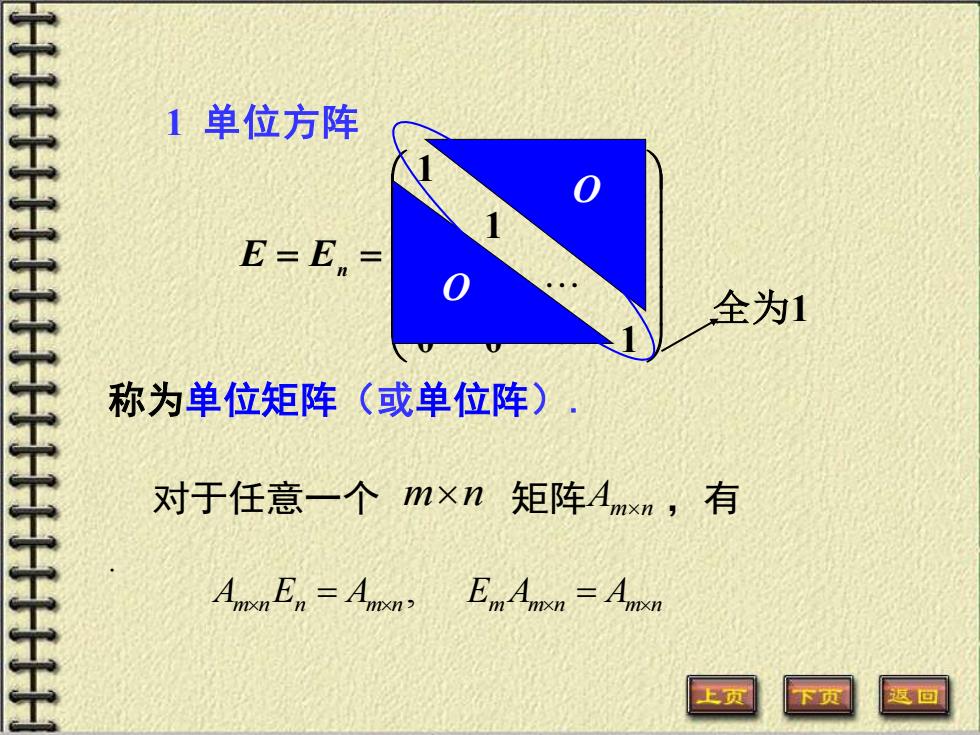
1单位方阵 E-E,= 全为1 称为单位矩阵（或单位阵) 对于任意一个m×n矩阵Amxn,有 Anpon En=Ancn Fm Angon=Aopn 上页

1 单位方阵             = = 0 0 1 0 1 0 1 0 0        E En 称为单位矩阵（或单位阵）. O O . 全为1 AmnEn = Amn Em Amn = Amn , 对于任意一个 mn 矩阵Amn ，有

特别当A是n阶方阵时AE=EA 2.对角阵 40 0 0 az 0 diag(a,a2,,a)= 0 0 an)nxn diag(a,az,,a)tdiag(b,b2,..,b) =diag(a1±b,a2±b2,,an±bn) 上页 这回

特别当 A 是 n 阶方阵时 A E = E A 2. 对角阵 ( ) n n n n a a a diag a a a                =         0 0 0 0 0 0 , , , 2 1 1 2 * ( ) ( ) ( ) n n n n diag a b a b a b diag a a a diag b b b =     , , , , , , , , , 1 1 2 2 1 2 1 2   

kdiag (a1,a2,…,an）=diog(ka1,ka2,…,kan) diag(a az,aliag(,bb) =diag(b:b2,..,b)diag(a,az: .…,an） =diag(ab:ab2,,a,b) (diag(a,a,,an》m=diaga,a,,a） 米 (aE)A=a(EA)=a(AE)=A(aE) 上页

( ) ( ) n n kdiag a , a , , a diag ka , ka , , ka 1 2  = 1 2  ( ) ( ) ( ) ( ) ( ) n n n n n n diag a b a b a b diag b b b diag a a a diag a a a diag b b b , , , , , , , , , , , , , , , 1 1 2 2 1 2 1 2 1 2 1 2      = = * ( ) ( ) m n m m m n (diag a, a , , a ) diag a , a , , a 2  = 1 2  * (aE)A = a(EA) = a(AE) = A(aE)

3三角阵 上三角阵 下三角阵 a111 a12 … a1 d22 A= a21 an2 上页 这回

3 三角阵 上三角阵 下三角阵               = n n n n a a a a a a A 0 0 0 0 22 2 111 12 1                     = an an an n a a a A        1 2 21 22 11 0 0 0 0

4转置矩阵 定义 把矩阵A 的行换成同序数的列得到的新矩阵，叫 做A 的转置矩阵，记作A a11 412 … ain a21 am A= a22 AT= a2 am2 am2 … a2n amn 上页

4 转置矩阵 定义 把矩阵 A 的行换成同序数的列得到的新矩阵，叫 做 A 的转置矩阵，记作 T A               = n n mn m m T a a a a a a a a a A        1 2 12 22 2 11 21 1               = m m mn n n a a a a a a a a a A        1 2 21 22 2 11 12 1

例 1 B=(18 6 18 上页 这回

例 , 4 5 8 1 2 2       A = ; 2 8 2 5 1 4           = T A B = (18 6), . 6 18      = T B

转置矩阵的运算性质 ()(4y=生 (2)(A+B)'=A+B; (3)(24)'=24'; (4)(AB)'=BA 上页

转置矩阵的运算性质 (1) (A ) A; T T = (2)( ) ; T T T A+ B = A + B (3)( ) ; T T A = A (4)( ) . T T T AB = B A

例5 已知 17 求(4B). 解法1 7、 :AB- -3 10 上页 区回

例5 已知 , 2 0 1 4 2 3 1 7 1 , 1 3 2 2 0 1           −  =      − A = B ( ) . T 求 AB 解法1           −       − = 2 0 1 4 2 3 1 7 1 1 3 2 2 0 1  AB , 17 13 10 0 14 3       − = ( ) . 3 10 14 13 0 17           −  = T AB

解法2 (AB)=BAT 4 2 17 = -3 30 上页

解法2 ( ) T T T AB = B A           −           − = 1 2 0 3 2 1 1 3 1 7 2 0 1 4 2 . 3 10 14 13 0 17           − =