第四节矩阵秩与向量组秩的关系 ☒无法显示该图片 1 2 设A= 02N 02 是mxn的矩阵 m2 mn
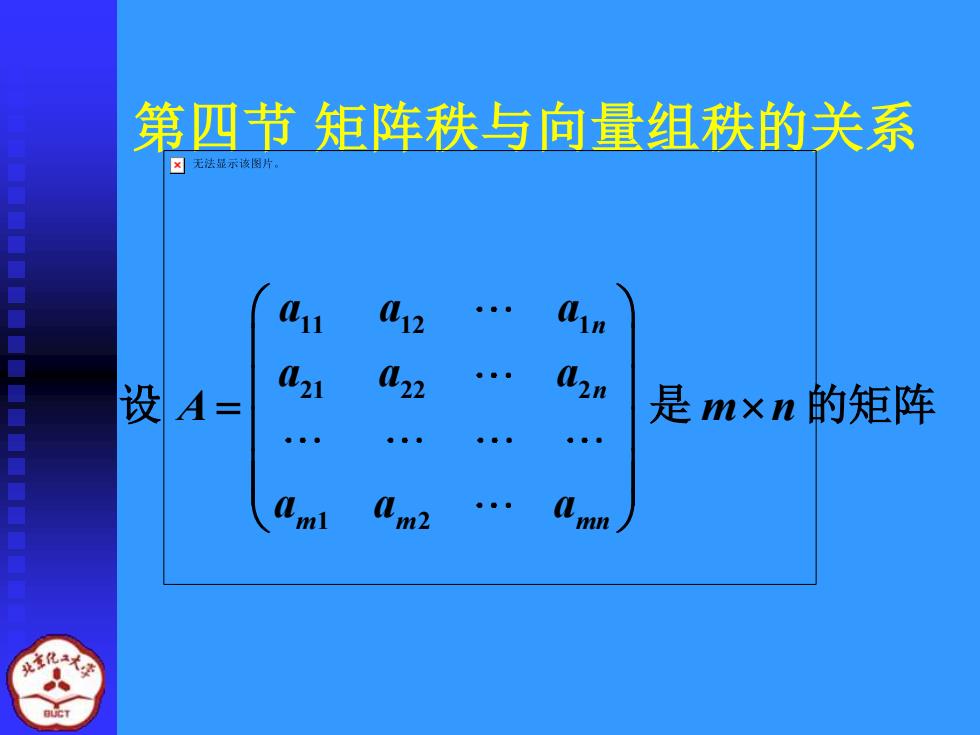
第四节 矩阵秩与向量组秩的关系 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A m n a a a = 设 是 的矩阵

按行分块得到 A= B. 其中p=(a1,42,…un) 是A的第行构成的向量 (年1,2,…m
按行分块得到 1 2 m A = ( ) ( ) 1 2 , , i i in a a a A i 其中 i = 是 的第 行构成的向量 i= 1,2, m

将该矩阵按列分块得到 A=(aag2… j 其中0,= 是A的第例构成的 向量(手1,2,…n)
将该矩阵按列分块得到 A= ( 1 2 n ) 1 2 j j j mj a a a = 其中 ( ) A n 是 的第j列构成的 向量 j= 1,2

{f,…pnm} 称为A的行向量组 {ap…on} 称为A的列向量组 定义9矩阵A的行向量组的秩成为A 的行秩,A的列向量组的秩称为A的 列秩。 矩阵A的秩与其行秩和列秩有 什么关系呢?
称为A的行向量组 1 , m n 1 , 称为A的列向量组 定义9 矩阵A的行向量组的秩成为A 的行秩,A的列向量组的秩称为A的 列秩。 矩阵A的秩与其行秩和列秩有 什么关系呢?

先看一个例子 0 B 此矩阵为具有4个非零行的 B-型矩阵
先看一个例子 1 1 2 2 3 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 a b a b B b = 此矩阵为具有4个非零行的 B-型矩阵

R(B)=4 显然B的列向量组B,阝2,B,B。 线性无关,并 B3=4B1+42B, Bs=bB+b2B2+b3B 故阝,P2,B,B。 是B的列向量组的极大无关组
R B( ) = 4 显然B的列向量组 1 2 4 6 , , , 线性无关,并且 3 1 1 2 2 5 1 1 2 2 3 3 a a b b b = + = + + 故 1 2 4 6 , , , 是B的列向量组的极大无关组

般的,对有个非零行的B-型阶梯 型矩阵,有 B的列秩=B的秩=4 B的列秩=B的秩=r 引理设矩阵A经过行初等变换化为B, 分别记为:A=(01,2,n) B=(β,B2,Bn》
B的列秩=B的秩=r 一般的,对有r个非零行的B-型阶梯 型矩阵,有 B的列秩=B的秩=4 引理 设矩阵A经过行初等变换化为B, 分别记为: 1 2 ( , ,..., ) A = α α αn B = (β β β 1 2 , ,..., n )

则A的列向量组与B的列向量组 之间有完全相同的线性关系,即 y01+X202+..+Xnn=0 当且仅当xB1+x2B2+.+xBn=0 证因为矩阵A经过行初等变换化为 B,A的列向量组与B的列向量组等 价,也就是说齐次线性方程组AX=0 与BX=0同解,即
之间有完全相同的线性关系,即 则A的列向量组与B的列向量组 1 1 2 2 α α α 0 ... n n x x x + + + = 当且仅当 1 1 2 2 ... n n x x x β + + + = β β 0 证 因为矩阵A经过行初等变换化为 B,A的列向量组与B的列向量组等 价,也就是说齐次线性方程组AX=0 与BX=0同解,即

¥01+X202+..+x,0n=0与 xB1+x2B2+…+xnBn=0同解 于是知列向量组 01,02,0n与B1,B2,B, 有相同的线性相关性
有相同的线性相关性。 于是知列向量组 1 2 , ,..., α α αn 与 1 2 , ,..., β β βn 1 1 2 2 ... n n x x x β + + + = β β 0 同解 1 1 2 2 ... n n x x x α + + + = α α 0 与

定理5矩阵的秩等于它的行秩,也等 于它的列秩。 证设矩阵A=(a,)mm (A)= B是与之对应的B-型阵 设A的r阶非零子式D.≠O 下证A的列向量组的秩为 D,所在的r列构成的m×P矩阵为
定理5 矩阵的秩等于它的行秩,也等 于它的列秩。 证 设矩阵 ( ij )m n a A = r r ( ) A = B是与之对应的B-型阵 设A的r阶非零子式 0 D r 下证A的列向量组的秩为r D r 所在的r列构成的 m r 矩阵为