北京化工大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵 第一节 高斯消元法与矩阵的初等变换

第二章矩阵 第一节 高斯消元法与矩阵的初等变换 第二节矩阵的运算 第三节特殊矩阵 第四节逆矩阵 第五节分块矩阵 第六节利用初等变换求逆矩阵 第七节矩阵的秩

第一节 高斯消元法与矩阵的初等变换 第二章 矩 阵 第二节 矩阵的运算 第三节 特殊矩阵 第四节 逆矩阵 第五节 分块矩阵 第六节 利用初等变换求逆矩阵 第七节 矩阵的秩

第一节 高斯消元法与矩阵的初等变换 消元法解方程 二、矩阵的定义 三矩阵的初等变换 四方程组的求解问题 五利用Gauss消员元法求解线性方程 六结论思考题

第一节 高斯消元法与矩阵的初等变换 一 消元法解方程 二、矩阵的定义 三 矩阵的初等变换 四 方程组的求解问题 六 结论 思考题 五 利用 Gauss 消员元法求解线性方程

第一节 高斯消元法与矩阵的初等变换 对于包含n个未知数n个方程的方程组，或未知数系数 成的行列式值是零的方程组的解的存在条件和解法和解 个数。 一般考虑n个方程几个未知数的线性方程组 aux+a2x2+...+arnx=b azax2+az=b2 () amx+am2x2+amnxnbm

第一节 高斯消元法与矩阵的初等变换 对于包含 个未知数 个方程的方程组，或未知数系数形 成的行列式值是零的方程组的解的存在条件和解法和解的 个数。 一般考虑 个方程 个未知数的线性方程组 (1) 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1        + + + = + + = + + + = m m m n n m n n n n a x a x a x b a x a x a x b a x a x a x b        n n m m n

+3x=-2 X1 X2 X3 b 乃-x=1 1 0 3 -2 0=b+3 (3) 0 1 -1 1 0 0 0 b+3 方程组(3)是方程组(2)同解的梯形方程组。 如果b≠-3方程组(3)无解，从而方程组(2)无 解。当b=-3时，方程组(3)改写为 x1=-2-3x9 x2= 1+x3 其中变量x3可自由选取， 令x3-k 代入上式，得到 上页

     = + − = + =− 0 3 1 3 2 2 3 1 3 b x x x x (3) 0 0 0 3 0 1 1 1 1 0 3 2 1 2 3 + − − b x x x bi 方程组(3)是方程组(2)同解的梯形方程组。 如 果 b  −3 方程组(3)无解，从而方程组(2)无 解。当 b = −3 时，方程组(3)改写为    = + = − − 2 3 1 3 1 2 3 x x x x 其中变量 3 x 可自由选取， 令 x = k 3 代入上式，得到

消元法解方程 1.变换两个方程的位置： 2.用非零常数乘某一个方程； 3.将某一个方程的常数倍加到另一个 方程上。 上述三种变换称为线性方程组的初等变换。初等变换 可逆，方程组(1)经过上述三种初等变换后得到的新方程 组与方程组(1)有相同的解，即方程组的初等变换是方程 组的同解变换。 上页

消元法解方程 1. 变换两个方程的位置； 2. 用非零常数乘某一个方程； 3. 将某一个方程的常数倍加到另一个 方程上。 上述三种变换称为线性方程组的初等变换。初等变换 可逆，方程组(1)经过上述三种初等变换后得到的新方程 组与方程组(1)有相同的解，即方程组的初等变换是方程 组的同解变换

x1+2x2+x3=0 X2 X3 bi 例1 (2)对应系数 2 1 0 2x1+5x2+3=1 2 5 11 -3x2+3x3=b 0-33b 用-2乘第一个方程后加到第二个方程上，得到 x1+2x2+x3=0 X1 X2 X3 b 1210 x2-x1=1 01 -11 -3x2+3x3=b 0-3 用-2乘第二个方程后加到第一个方程上；再用3乘第二 个方程后加到第三个方程上，得到 这回

例 1      − + = + + = + + = x x b x x x x x x 2 3 1 2 3 1 2 3 3 3 2 5 1 2 0 (2) 对应系数 b x x x bi 0 3 3 2 5 1 1 1 2 1 0 1 2 3 − 用− 2乘第一个方程后加到第二个方程上，得到      − + = − = + + = x x b x x x x x 2 3 2 1 1 2 3 3 3 1 2 0 b x x x bi 0 3 3 0 1 1 1 1 2 1 0 1 2 3 − − 用− 2乘第二个方程后加到第一个方程上；再用3乘第二 个方程后加到第三个方程上，得到

x1=-2-3k x2=1+k 由常数的任意性可知，方程 x3=k 组(2)有无穷多解。 将方程组系数的变化用数表表示成下面的形式 12101210103-2 2511￥01-11-￥01-1 1 0-33b0-33b000b+3

将 方 程 组 系 数 的 变 化 用 数 表 表 示 成 下 面 的 形 式           + − − →           − → −           − 0 0 0 3 0 1 1 1 1 0 3 2 0 3 3 0 1 1 1 1 2 1 0 0 3 3 2 5 1 1 1 2 1 0 b b b      = = + = − − x k x k x k 3 2 1 1 2 3 由常数k 的任意性可知，方程 组(2)有无穷多解

二、矩阵的定义 由m×n个数a,(i=1,2,,m;j=1,2,…,n) 排成的m行n列的数表 L11 012 L21 L22 2… 称为行n列矩阵.简称mxn矩阵.记作 上页 这回

二、矩阵的定义 由 个数 排成的 行 列的数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 m 行 n 列矩阵.简称 mn 矩阵. 记作

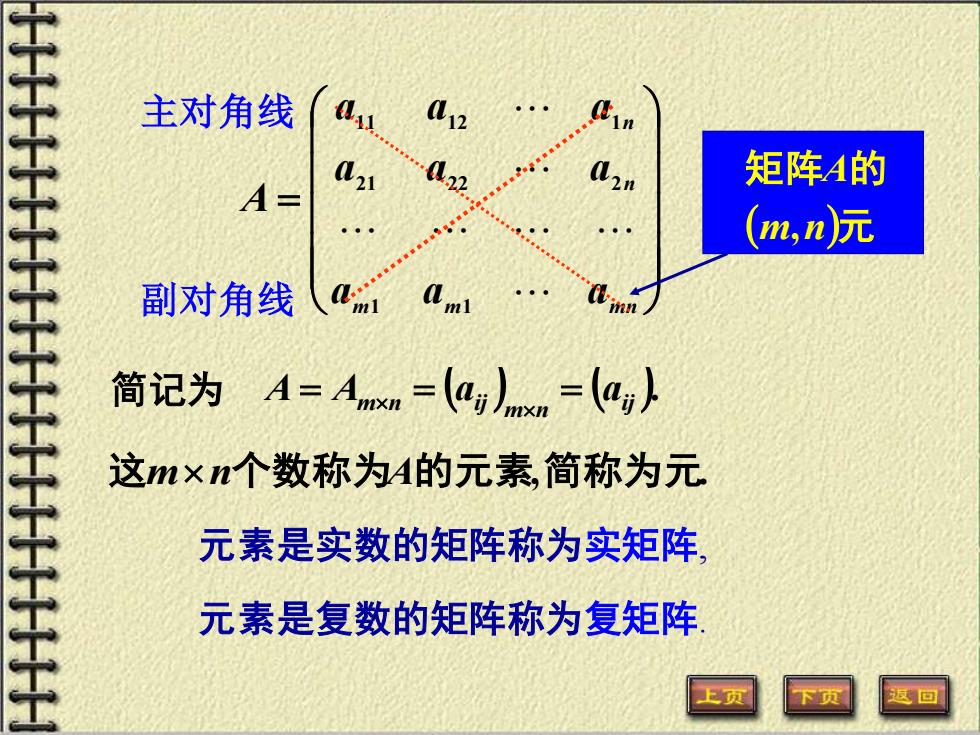
主对角线 矩阵4的 A (m,n元 副对角线 简记为A=Axn=(a与nm=(a,) 这m×n个数称为A的元素，简称为元 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵

              = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 简记为 ( ) ( ). ij m n A = Am n = aij = a   ( )元 矩阵 的 m n A , 这mn个数称为A的元素,简称为元. 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵. 主对角线 副对角线

例如 03 643 是一个2×4实矩阵， 136 21 2 2 2 是一个3×3复矩阵， 、22 2) 124 是一个3×1矩阵， (2359) (4) 是一个1×4矩阵， 是一个1×1矩阵 回

例如       − 9 6 4 3 1 0 3 5 是一个 24 实矩阵,           2 2 2 2 2 2 13 6 2i 是一个 33 复矩阵,           4 2 1 是一个 31 矩阵, (2 3 5 9) 是一个 14 矩阵, (4) 是一个 11 矩阵