
多变量函数的连续性
多变量函数的连续性
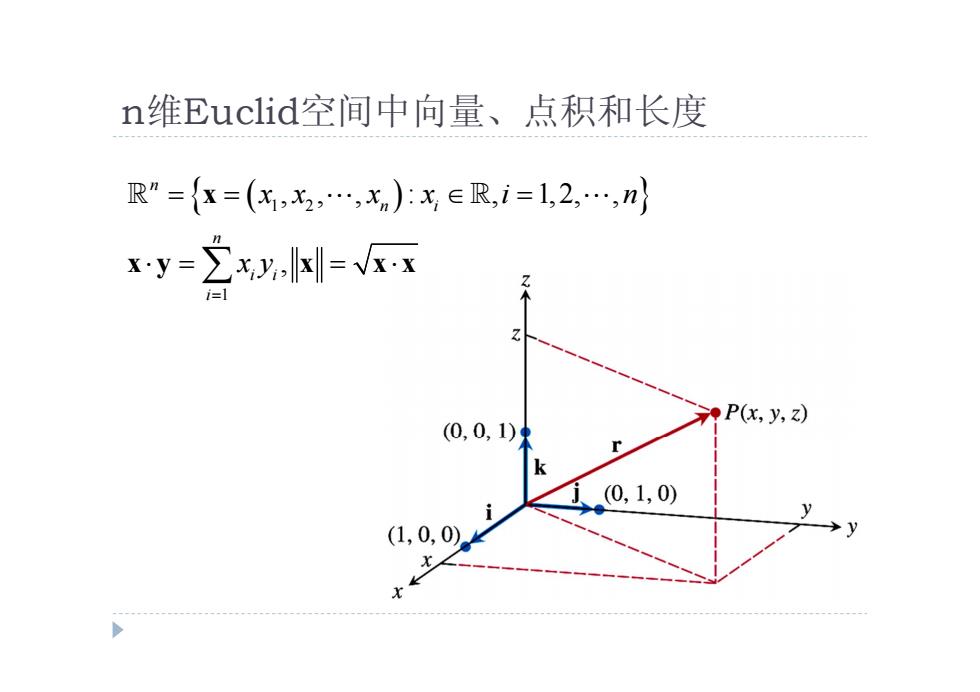
n维Euclid空间中向量、点积和长度 R”={x=(x,x,…,x)x∈R,i=1,2…,n} y=立y,小= P(x,y,z) (0,0,1) (0,1,0) (1,0,0) →y X
n维Euclid空间中向量、点积和长度 1 2 1 , , , : , 1,2, , , n n i n i i i x x x x i n x y x x y x x x
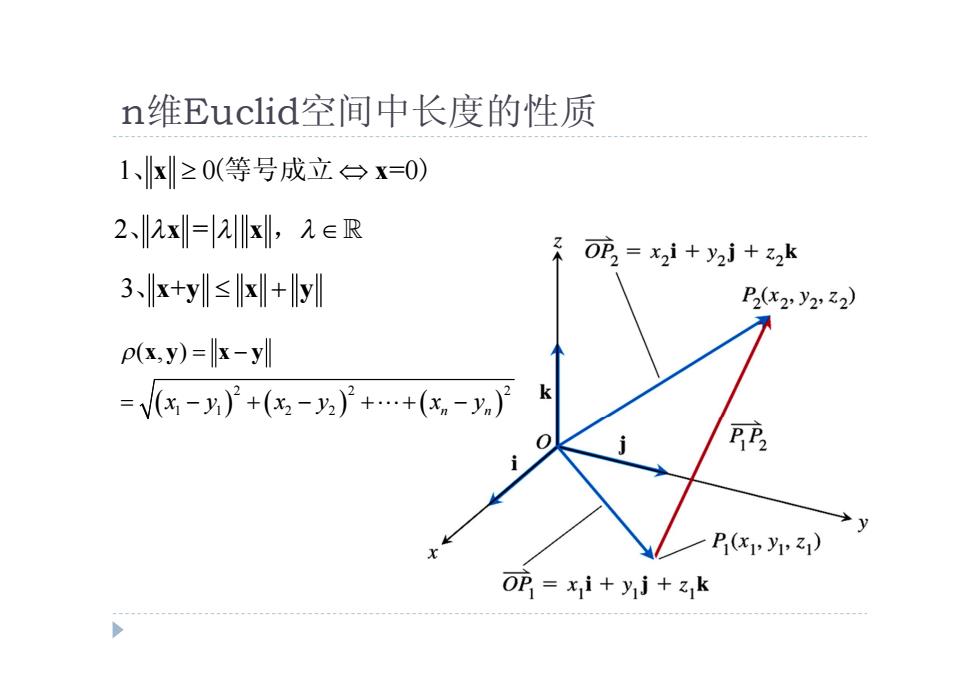
n维Cuclid空间中长度的性质 1、x≥0(等号成立台x=0) 22x=2x,元∈R 0m2=x21+y21+22k 3x+y≤✉+Il P2(x2y2:z2) p(飞,y)=k-y列 =V(x-y)+(x-乃)+…+(x,-y)月 k x1乙1) OP=xi+yj+zk
n维Euclid空间中长度的性质 1 0 =0 、x x (等号成立 ) 2 = 、 x x , 3 + 、x y x y 2 2 2 1 1 2 2 ( , ) n n x y x y x y x y x y

例 1、一个6牛顿的力F作用在向量v=2i+2j-k的方向上,把F表示成它的长度和方 向的乘积 2、求u=6i+3j+2k在v=i-2j-2k上的向量投影和u在方向v的数量分量
例 1、一个6 2 2 牛顿的力F v i j k F 作用在向量 = 的方向上,把 表示成它的长度和方 向的乘积 2 2 2 2 1 6 6 6 9 3 3 3 v i j k F i j k v 2 6 3 2 2 2 、求u i j k v i j k u v 在 上的向量投影和 在方向 的数量分量 2 4 8 8 proj cos cos 9 9 9 4 cos 3 v u v u u u v i j k v u v u v v v v v v v
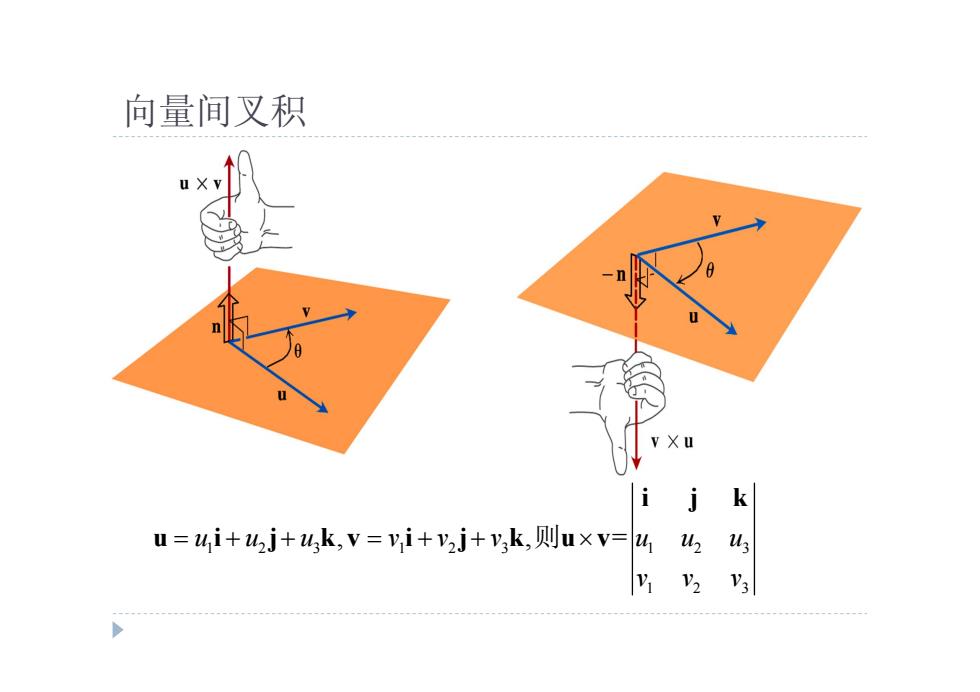
向量间叉积 i j k u=u,i+2j+4k,V=yi+y2j+yk,则u×v=
向量间叉积 1 2 3 1 2 3 1 2 3 1 2 3 u u u v v v u u u , , = v v v i j k u i j k v i j k u v 则
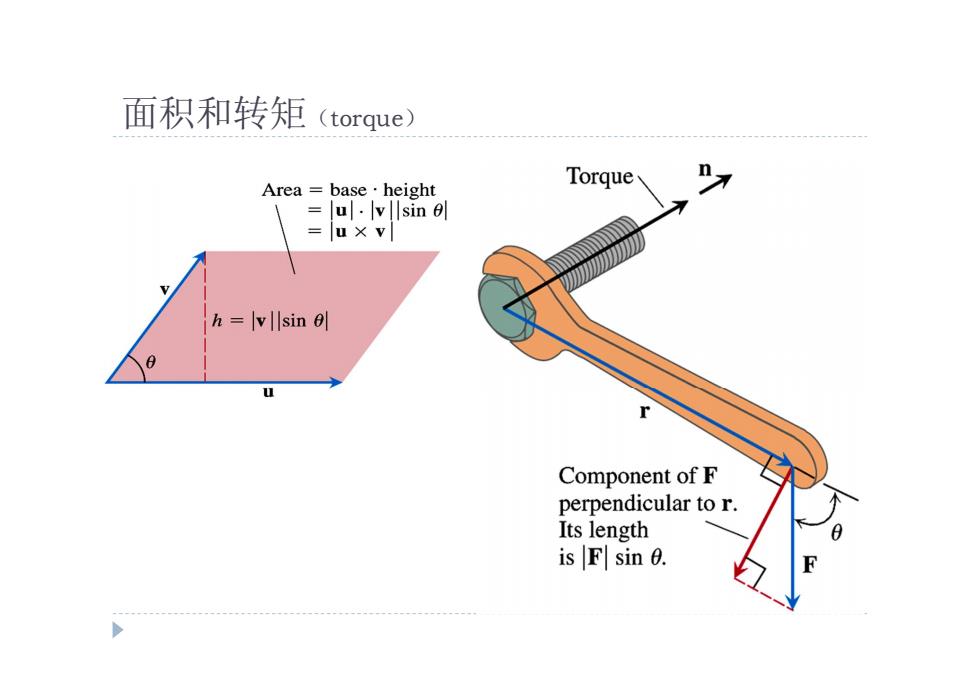
面积和转矩(torque) Area=-base·height Torque u.v sin =u x v h=vsin Component of F perpendicular to r. Its length is F sin 0
面积和转矩(torque)
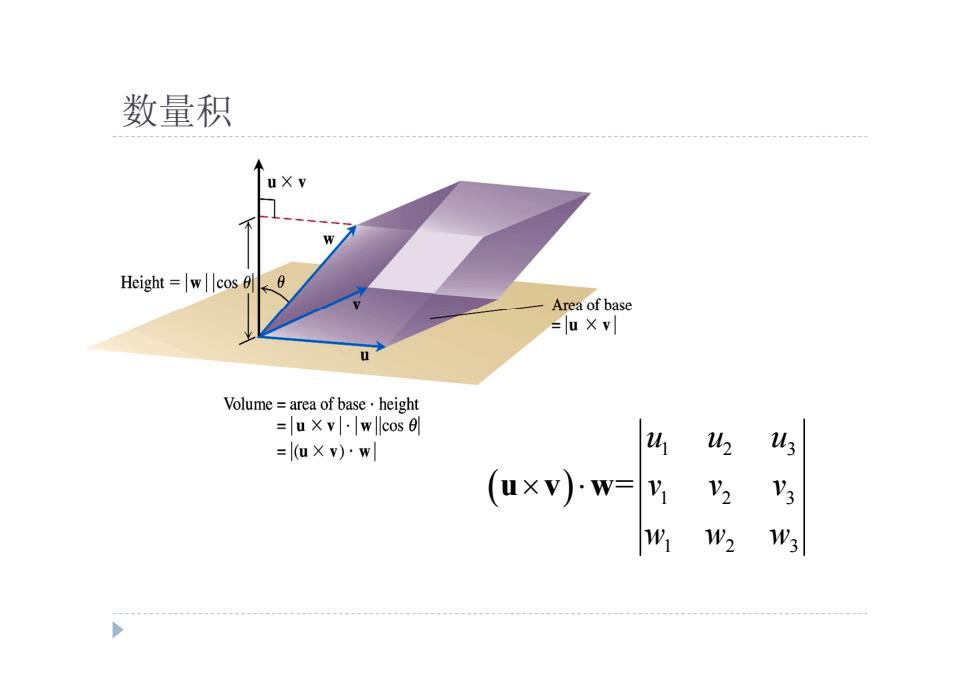
数量积 Height =wcos0 Area of base =u X v Volume=area of baseheight =lu×v|·wllcos =lu×)·w u 23 (uxv)w= w W2 W3
数量积 1 2 3 1 2 3 1 2 3 = u u u v v v w w w u v w
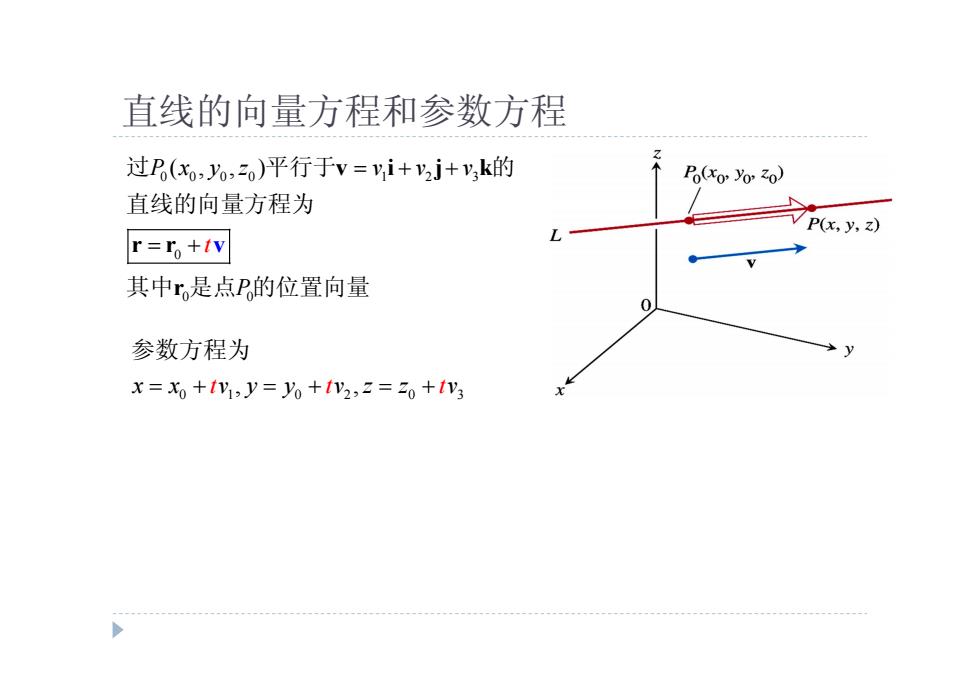
直线的向量方程和参数方程 过P(xo,yo,平行于v=yi+2j+y,k的 Po(xo Yo Zo) 直线的向量方程为 VP(x,y,z) r=r。+w 其中r是点P的位置向量 参数方程为 x=xo+1y,y=yo+1v2,2=20+1v3
直线的向量方程和参数方程 0 0 0 0 1 2 3 0 0 0 P x y z v v ( , , ) t v P v i j k r r v r 过 平行于 的 直线的向量方程为 其中 是点 的位置向量 0 1 0 2 0 3 x x v y y t t t , , v z z v 参数方程为

空间中平面的方程 过点P(o,o,二)且垂直于n=Ai+Bj+Ck的平面有 向量方程:nP。P=0 分量方程:A(x-x)+B(y-y)+C(z-2)=0 简化分量方程:Ax+By+Cz=D, (其中D=Ax+By+C) Plane M P(x,y,2) w
空间中平面的方程 0 0 0 0 0 0 0 0 0 0 0 ( , , ) P 0 ( ) ( ) ( ) 0 , ( P x y z A B C P A x x B y y C z z Ax By Cz D D Ax By Cz n i j k n 过点 且垂直于 的平面有 向量方程: 分量方程: 简化分量方程: 其中 )
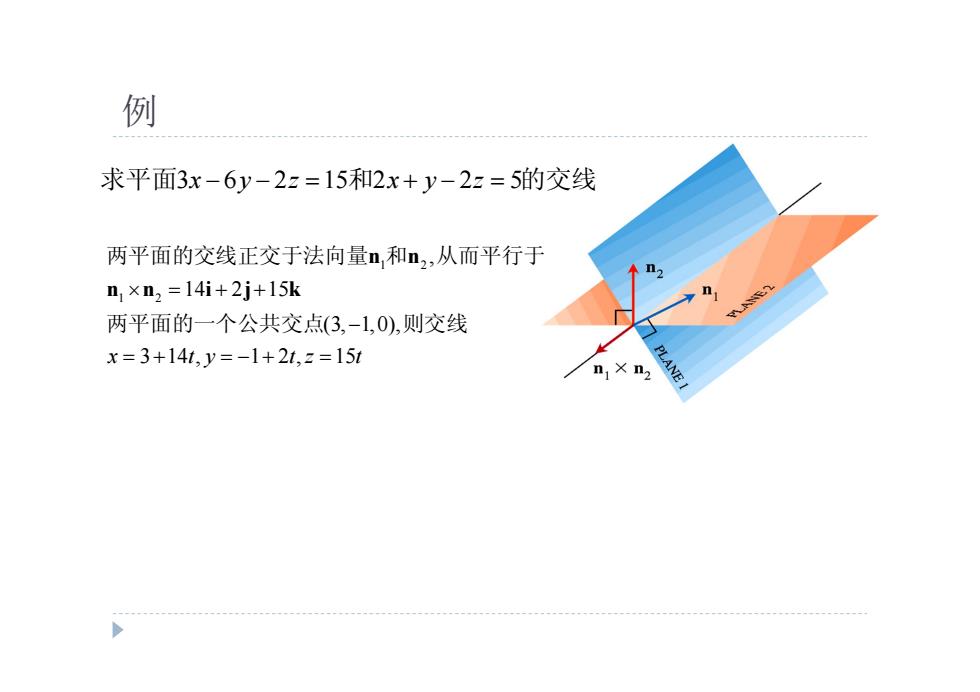
例 求平面3x-6y-2z=15和2x+y-2z=5的交线 两平面的交线正交于法向量n,和n,从而平行于 n,×n2=14i+2j+15k 两平面的一个公共交点(3,-1,0),则交线 x=3+14t,y=-1+2t,z=15t n1×n2 ANE
例 求平面3 6 2 15 2 2 5 x y z x y z 和 的交线 1 2 1 2 , 14 2 15 (3, 1,0), x t y t z t 3 14 , 1 2 , 15 n n n n i j k 两平面的交线正交于法向量 和 从而平行于 两平面的一个公共交点 则交线