函数的积分
函数的积分
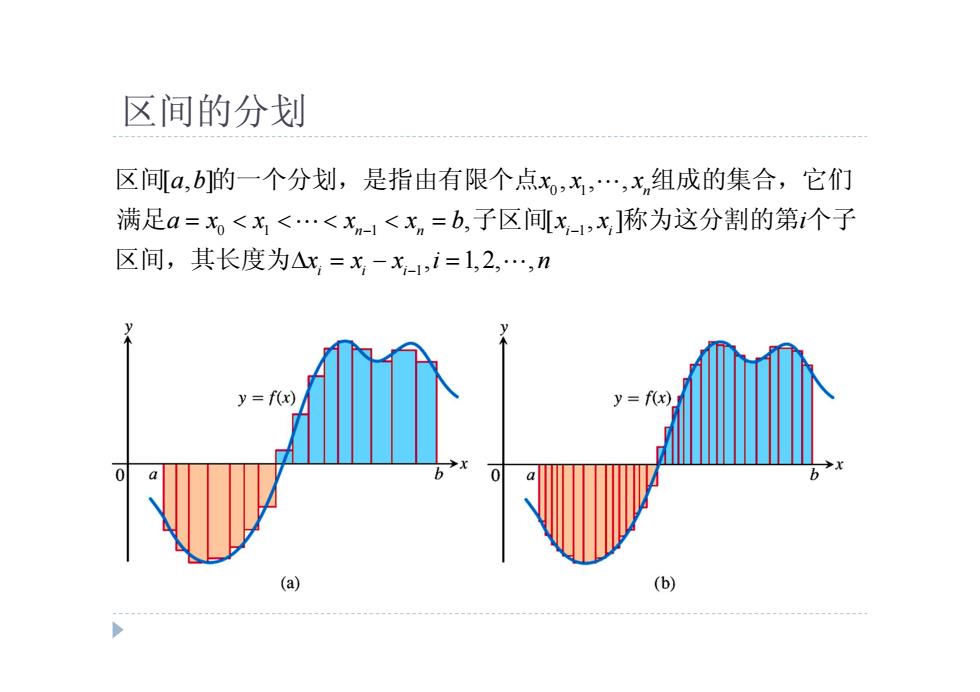
区间的分划 区间[a,b的一个分划,是指由有限个点x,x,…,x,组成的集合,它们 满足a=x<x<<x-1<,=b,子区间[x-1,x]称为这分割的第个子 区间,其长度为△x,=x,-x-,i=1,2,…,n y=f(x) y=f(x) 0 b 0 b (a) (b)
区间的分划 0 1 0 1 1 1 1 [ , ] , , , , [ , ] , 1, 2, , n n n i i i i i a b x x x a x x x x b x x i x x x i n 区间 的一个分划,是指由有限个点 组成的集合,它们 满足 子区间 称为这分割的第 个子 区间,其长度为
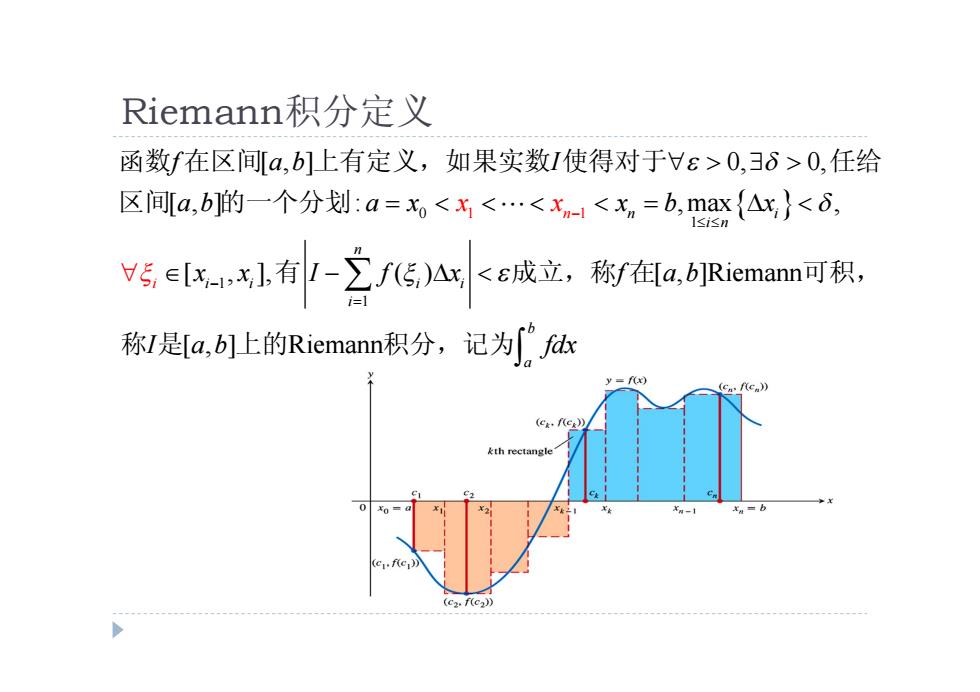
Riemann积分定义 函数f在区间[a,b]上有定义,如果实数I使得对于Vε>0,δ>0,任给 区间[a,b]的一个分划:a=x<x<…<xn-1<x,=b,max{Ax}<d, V发ck1有-立GA<e成立,称.Riemamt可积, 称I是[a,b]上的Riemann积分,记为fr =x c.(C kth rectangl (cfc2》
Riemann积分定义 0 1 1 1 1 1 [ , ] 0, 0, [ , ] : ,max , [ , ], ( ) [ , ]Riemann [ , ] Riemann n i i n n i i i i i i b a n f a b I a b a x x b x x x I f x f a b I a dx x x b f 函数 在区间 上有定义,如果实数 使得对于 任给 区间 的一个分划 有 成立,称 在 可积, 称 是 上的 积分,记为

可积函数的有界性 f在[a,b]可积,则f在[a,b]有界 取=l,存在分划△:a=x<x<<x-1<xn=b,5,∈[xX,] 满足:1-立A<1,即它八A<川+L进而有 sX<+1+2G数G+1+空G 固定5,i=2,3,,n,立即得到f在[x,x]区间上的有界性,同理可得 在[x-x,](i=2,3,…,n)区间上的有界性,从而得到f的有界性
可积函数的有界性 f a b f a b 在[ , ] [ , ] 可积,则 在 有界 0 1 1 1 1 1 1 1 1 2 2 1 0 1 1 =1 , [ , ], ( ) 1 ( ) 1, 1 ( ) 1 ( ) , ( ) 1 ( ) , , 2,3, , , [ , ] [ , n n i i i n n i i i i i i n n i i i i i i i i i a x x x x b x x I f x f x I f x I f x f I f x x i n f x x f x x 取 ,存在分划 : 满足: ,即 进而有 故 固定 立即得到 在 区间上的有界性,同理可得 在 ] 2,3, , i n f 区间上的有界性,从而得到 的有界性

函数的振幅、Darboux上和、下和 给定区间[a,b]和定义在其上的有界函数f(x),f在[a,b]上的上下确界分别 为M,m,令o=M-m称为f在[a,b]区间上的振幅 给定区间[a,b的一个分割△:a=x。<x<…<xn1<xn=b,在每个子区间 [x-,x]上f的上下确界分别记为M,m,并令o,=M,-m,称之为f在子区间 [xx止的振幅,定义5=∑MAx,S=∑mAx 份别称为f关于分割△ 的Darboux.上和Darboux下和
函数的振幅、Darboux上和、下和 0 1 1 1 1 1 1 [ , ] ( ) [ , ] , , [ , ] [ , ] , [ , ] , , [ , ] , n n i i i i i n n i i i i i i i i i i a b f x f a b M m f a b a b a x x x x b x x f M m M m f x M m x f S M x S m x 给定区间 和定义在其上的有界函数 , 在 上的上下确界分别 为 令 称为 在 区间上的振幅 给定区间 的一个分割 : 在每个子区间 上 的上下确界分别记为 并令 称之为 在子区间 上的振幅,定义 分别称为 关于 Darboux Darboux 分割 的 上和 下和

区间分划的加细和上下和的关系 设分划:a=<x<…<x1<xn=b,子区间[x-1,x]长度记为△g=x,-x, 在上述分划基础上再增加一个分点,称为分划的加细。不失一般性,可设 在第个区间内增加一个分点x,即=x<…<x<x<x,<…<xn=b,此时, 前者下和中的一项m△被后者(-x小()+(区-x)/(✉所代替, 但(x-EJ因)+(飞-)f)2(-m+(飞-)m=mA 由此下和随分划的加细而单调上升,同理上和随分划的加细而单调下降。 Darboux.上和的下确界称为f在a,b]上的上积分5,Darboux下和的上确 界称为f在a,b]上的下积分3,由上下和随分划加细的单调性,有 mS=3, lim S -3
区间分划的加细和上下和的关系 * * 1 0 1 1 1 1 * * 0 1 * * 1 , , * 1 , [ , ] , , inf inf i i i n n i i i i i i i n i i i i x x x x i a x x x x b x x x x x i x x x x x x b m x x x f x x x f x x x 设分划: 子区间 长度记为 在上述分划基础上再增加一个分点,称为 。不失一般性,可设 在第 个区间内增加一个分点 ,即 此时, 前者下和中的一项 被后者 所代替, 但 分划的加细 * * 1 * * * 0 1 , , 0 nf inf = Darbou lim lim x [ , ] Darboux [ , ] i i i i i i i i i x x x x f x x x f x x x S m x x m m x f a b a S f b 由此 ,同理 。 上和的下确界称为 在 上的上积分 , 下和的上确 界称为 在 上的下积分 ,由上下和随分划加细的单调性, 下和随分划的加细而单调上升 有 上和随分划的加细而单调下降

例(Darboux.上下和) 1.0时 0.75 0.75 05 0.5 025 025 00+ 00 025 05 075 10 00 0.25 0.5 07570 10y 10 0.75 0,75 02 0.25 00+ 0 00 0.25 05075 10 00 05 0.75 1.0
例(Darboux上下和)

Gaston Darboux 达布(Darboux),(1842-1917)法国数学家.Darboux 的主要贡献在数学分析,微分几何,微分方程等领 域。在数学分析方面,他给出了一个“病态函数” 当自变量x=a变到=b时,这个函数取遍了两个给 定值之间的一切中间值,但却是不连续的。这使人 们对连续的概念有了更深入的理解,因为当时对 “连续性”还没有给出严格定义。在定积分理论中, 有以他的名字命名的“Darboux和”,上积分,下 积分等概念。他的工作对Riemann积分论的发展起 到了重要作用。在微分几何方面的两本专著:《曲 面通论教程》(1887-1896)和《正交系与曲线坐 标》(1898).书中系统地介绍了近百年来微分几何学 方面的成就,其中包括了很多他自己的研究成果。 在微分方程方面,他研究了微分方程的可积性及积 分法等问题。总结了Laplace级数方法,并应用于所 有二阶偏微分方程,还深入地研究了非线性方程的 Monge方法,建立了Darboux方程。此外他在解析 函数论,代数函数以及数学物理方程等方面都取得 了重要成果。1870年他创办了《数理科学通报》
Gaston Darboux 达布(Darboux),(1842-1917)法国数学家.Darboux 的主要贡献在数学分析,微分几何,微分方程等领 域。在数学分析方面,他给出了一个“病态函数”, 当自变量x=a 变到 x=b时,这个函数取遍了两个给 定值之间的一切中间值,但却是不连续的。这使人 们对连续的概念有了更深入的理解,因为当时对 “连续性”还没有给出严格定义。在定积分理论中, 有以他的名字命名的“Darboux和”,上积分,下 积分等概念。他的工作对Riemann积分论的发展起 到了重要作用。在微分几何方面的两本专著:《曲 面通论教程》(1887-1896)和《正交系与曲线坐 标》(1898).书中系统地介绍了近百年来微分几何学 方面的成就,其中包括了很多他自己的研究成果。 在微分方程方面,他研究了微分方程的可积性及积 分法等问题。总结了Laplace级数方法,并应用于所 有二阶偏微分方程,还深入地研究了非线性方程的 Monge方法,建立了Darboux方程。此外他在解析 函数论,代数函数以及数学物理方程等方面都取得 了重要成果。1870年他创办了《数理科学通报》

可积性条件 设函数f为区间可[a,b]上的有界函数,以下三个条件相互等价: f在[a,b]上可积 台 E>0,3δ>0,[a,b的-个分划,当max{Ax}<δ时,∑0,Ax<e 台 [a,b]上f的上下积分相等
可积性条件 [ , ] [ , ] f a b f a b 设函数 为区间 上的有界函数,以下三个条件相互等价: 在 上可积 1 1 0, 0 [ , ] max n i i i i n i a b x x , 的一个分划,当 时, [ , ] a b f 上 的上下积分相等

可积性条件的证明 如果f可积,设其积分值为1,则Vε>0,36>0,[a,b的一个分划: a=0,36>0,[a,b]的一个分划:a=x<x<…<xm=b, max{a<6,5,∈cx1.有2a,Ax<6,则 0≤5-S≤5-S=0,Ay<e,由e的任意性,5=3 如果[a,b]上f的上下积分相等,由于S≤∑f(5,)△x≤S,两边取极限即得
可积性条件的证明 0 1 1 1 1 1 1 1 , 0, 0 [ , ] : , max , [ , ], ( ) 3 2 3 3 3 n n i i i i i i i n i n n n i i i i i i i i i f I a b a x x x b x x x I f x I m x M x I x 如果 可积,设其积分值为 则 , 的一个分划 有 , 则 ,从而有0 0 1 1 1 1 1 0, 0 [ , ] : , max , [ , ], , n n i i i i i i i n i n i i i a b a x x x b x x x x S S x 如果 , 的一个分划 有 ,则 0 由 的任意性, 1 [ , ] ( ) n i i i a b f S f x S 如果 上 的上下积分相等,由于 ,两边取极限即得