一元微分学
一元微分学

瞬时速度 △、=等速运动所走的距离+重力加速度g引起的多走的距离 =G)+28(a 另外宜接由公式:A=方86+a0-方6=8既4+8(月 比较上面两式得到v(t)=gt
瞬时速度 2 2 2 2 0 0 0 0 0 0 + 1 2 1 1 1 2 2 2 ( ) ( = ) s g t g t s g t t gt t g t v t g v t t gt 等速运动所走的距离 重力加速度 引起的多走的距离 另外直接由公式: 比较上面两式得到
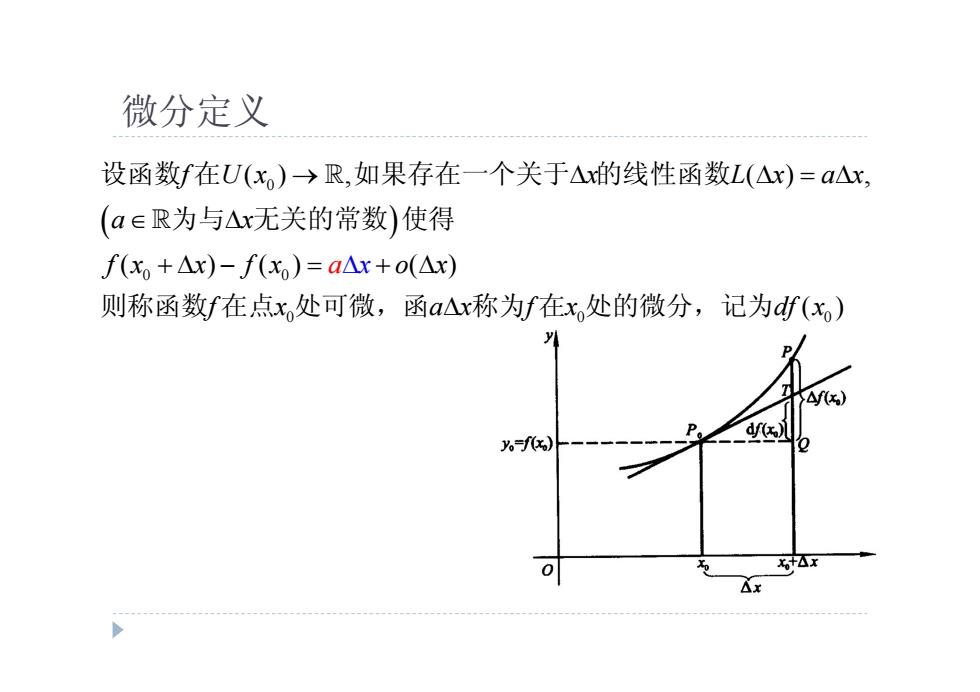
微分定义 设函数f在U(x)→R,如果存在一个关于△x的线性函数L(△x)=a△x, (a∈R为与△x无关的常数)使得 f(x,+△x)-f(x)=a△x+o(△x) 则称函数f在点x处可微,函a△x称为f在x,处的微分,记为df(x) d(x.) f3) 0
微分定义 0 0 0 0 0 0 ( ) , ( ) , ( ) ( ) ( ) ( ) f U x x L x a x a x a x f x x f x o x f x a x f x df x 设函数 在 如果存在一个关于 的线性函数 为与 无关的常数 使得 则称函数 在点 处可微,函 称为 在 处的微分,记为

可微与可导的关系 单变量函数f(x)在x处可导一f(x)在x处可微 证明:若y=f(x)在x处可导,则f(x+△x)-f(x)=f"(x)△x+o(△x), 故f在x处可微,且例6=∫'(xo)Ax 反之,如果f在x处可微,则f(x。+△x)-f(x)=a△x+o(△x),即 f飞+△)-f_aAx+o△,故fx,)=a △x △x 注:由可微与可导的关系,立即得到 df(x)=∫"(x)△x=f'(x)d,由此导数也记为 dx
可微与可导的关系 0 0 单变量函数f x x f x x ( ) ( ) 在 处可导 在 处可微 0 0 0 0 0 0 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) x x y f x x f x x f x f x x o x f x dy f x x f x f x x f x a x o x f x x f x a x o x f x a x x 证明:若 在 处可导,则 故 在 处可微,且 反之,如果 在 处可微,则 ,即 ,故 0 0 0 ( ) ( ) ( ) ( ) df df x f x x f x dx f x dx 注:由可微与可导的关系,立即得到 ,由此导数也记为
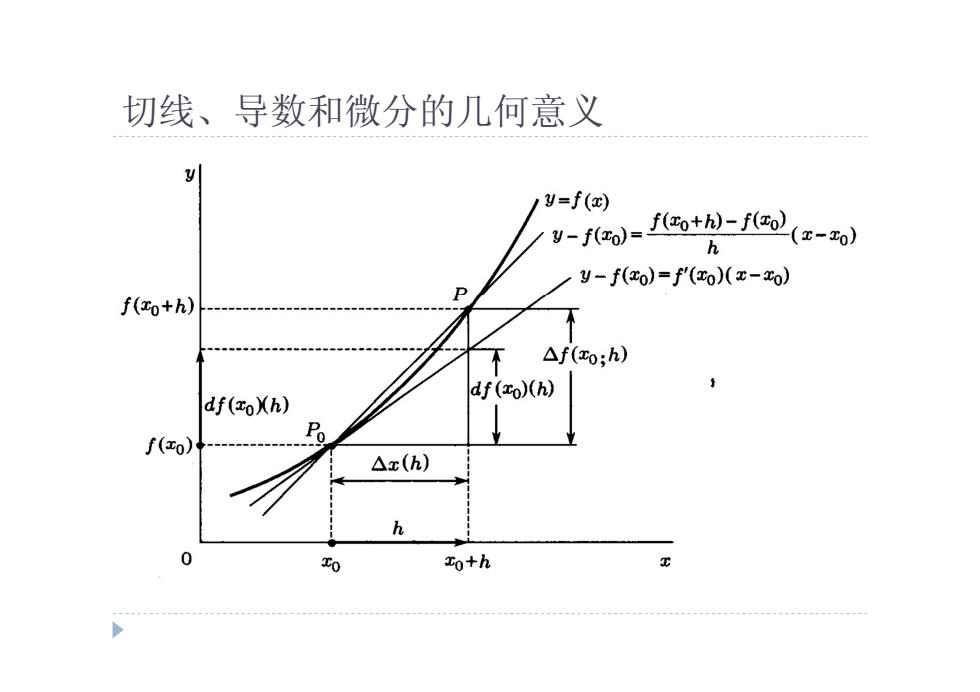
切线、导数和微分的几何意义 y y=f(x) y-fo-fo+h-f3o(x-0) h y-f(zo)=f'(xo)(x-Zo) P f(o+h) △f(xo;h) df (xo)(h) df(zoXh) f(xo) △x(h) h 0 xo+h
切线、导数和微分的几何意义

y=f(x) △f=fa+dx)-fa) △L=f'(a)dx (a,f(a)) dx When dx is a small change in x, Tangent the corresponding change in line the linearization is precisely df. →X 0 e a +dx
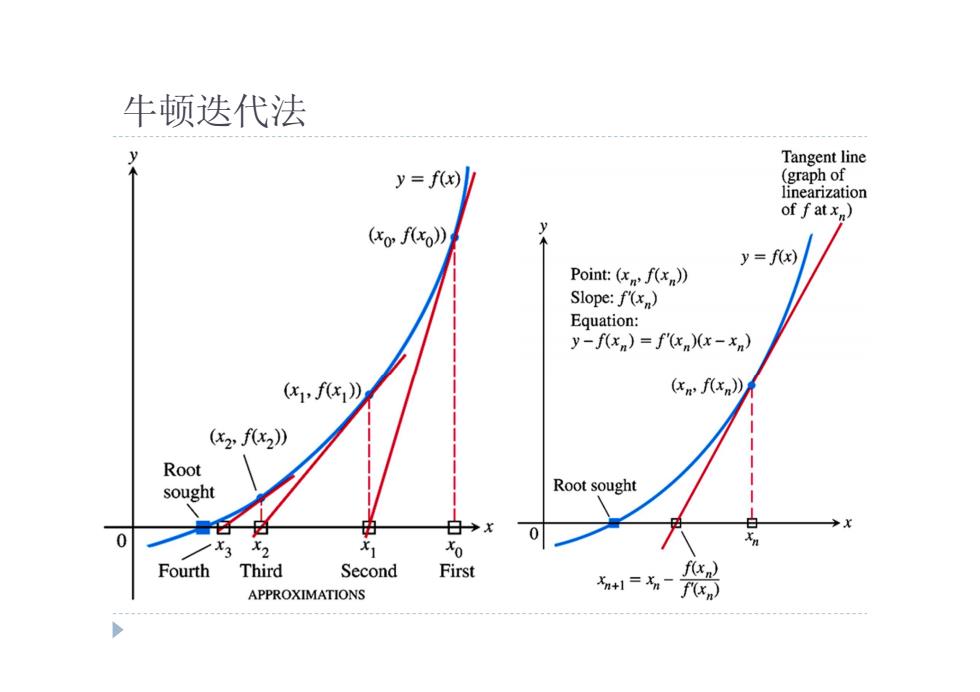
牛顿迭代法 Tangent line y=f(x)l (graph of linearization of f atxn) (xo f(xo)》 y=f(x) Point:(cn,fxn》 Slope:f(x) Equation: y-f(xn)=f(xn)(x-x) ,f) (xn f(xn)》 (2f0x2》 Root sought Root sought 日→x 0 3 0 0 Fourth Third Second First f(xn) APPROXIMATIONS ntl=n-f(xn
牛顿迭代法
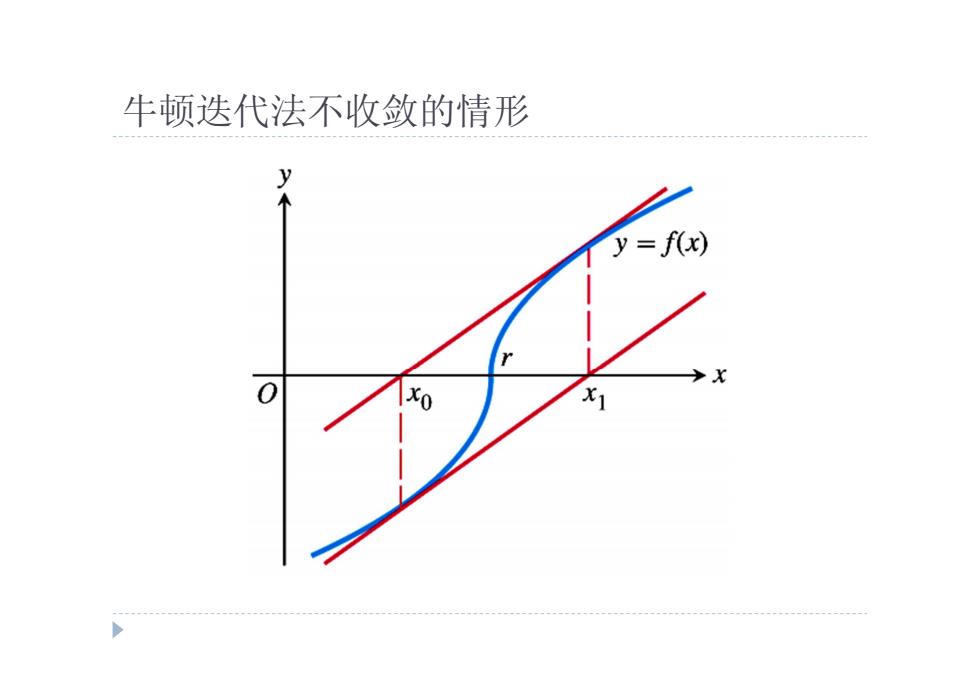
牛顿迭代法不收敛的情形 y y=f(x) 0 X
牛顿迭代法不收敛的情形
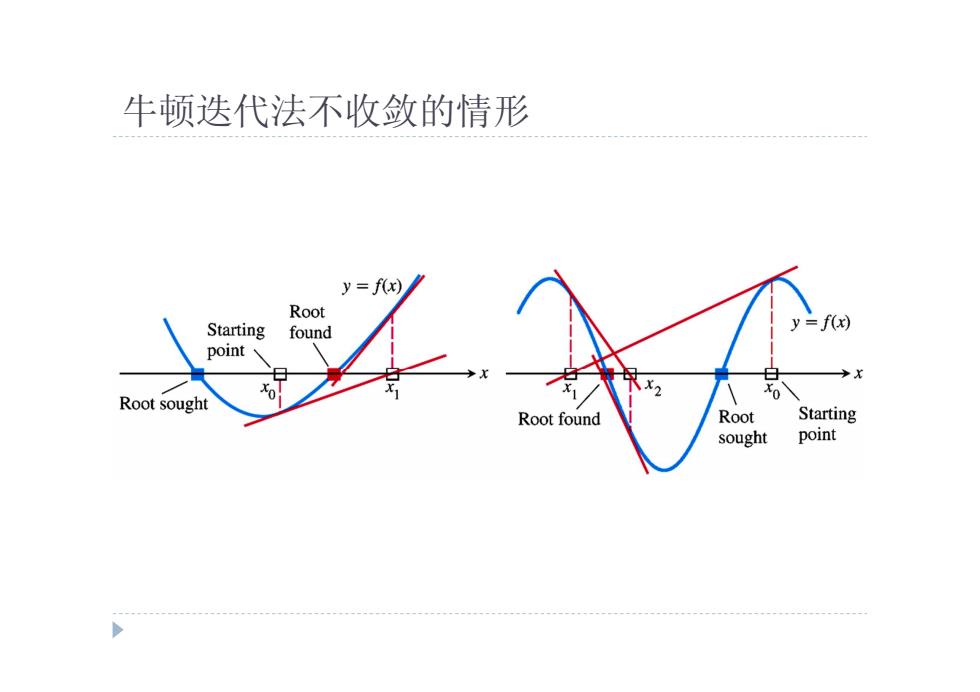
牛顿迭代法不收敛的情形 y=f(x) Root Starting =f(x) found point Root sought Root found Root Starting sought point
牛顿迭代法不收敛的情形

牛顿法求根的不确定性 y=4x4-4x2 RootA 2 Root B 2 7 Root C V21 2 (a) 6) 0 (c)
牛顿法求根的不确定性