函数的导数
函数的导数

例 细棒的线密度问题 0 +Ar1x ,平面的切线斜率问题 2 0 +△x
例 细棒的线密度问题 平面的切线斜率问题

万有引力定律和牛顿动力学定律 太阳S位于惯性坐标系(x,y,z)的原点O,而地球E的坐标向量为 r(t)=(x(t),y(t),z(t),E的运动速度和加速度分别为v(t)以a(t), 万有引力定律 f(t) G mme r(t) r(r(o ma=-Gmme r(t) 牛顿第二定律 r(02 r(t) ma f(t) 其中r(t)=Vx()2+y()2+z()2 v)=lm)-r,a6)=lim0)- 1-→0 1-to 1-→l0 1-to
万有引力定律和牛顿动力学定律 0 2 2 2 2 0 0 2 S ( , , ) O E ( ) ( ( ), ( ), ( )) E ( ) ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) li ( ) ( ) ( ) m s e e s e e t t x y z t x t y t z t t t m m t t G t t m t t x t y t z t t t t t m m t m G t t r v a r f r r a f r a r r r r r v 万有引力定律 牛顿第二定律 太阳 位于惯性坐标系 的原点 ,而地球 的坐标向量为 , 的运动速度和加速度分别为 、 其中 0 0 0 0 0 ( ) ( ) , ( ) lim t t t t t t t t v v a

导数定义 设函数f定义在x,的邻域U(xo)内,如果极限Iim f(x,+△x)-f(x) 存在,称 △r0 △x 这个极限值为在点的导数,记作或旷(国 ,并称函数f在x点可导。 Y=x 设函数f在一点x的右边[x,x。+δ)有定义,如果极限lim f(x,+△x)-f(x) △r-→0 △x 存在并且有限,称这个极限值为f在点x,的右导数,记作(x),并称函数 f在x点右可导。类似可定义左导数f'(x)。 如果函数f在开区间(a,b)中的每点可导,则称f在(a,b)上可导,如果 f在(a,b)上可导,在a点有右导数,在b点有左导数,则称f在闭区间 [a,b]上可导
导数定义 0 0 0 0 0 0 0 0 ( ) ( ) lim ( ) , x x x f x x f x U x d f f x f x f x f x x x x d 设函数 定义在 的邻域 内,如果极限 存在,称 这个极限值为 在点 的导数,记作 或 并称函数 在 点可导。 ( , ) ( , ) ( , ) [ , ] f a b f a b f a b a b f a b 如果函数 在开区间 中的每点可导,则称 在 上可导,如果 在 上可导,在 点有右导数,在 点有左导数,则称 在闭区间 上可导。 0 0 0 0 0 0 0 0 ( ) ( ) [ , ) lim ( ), ( ) x f x x f x f x x x x f x f x f x f x 设函数 在一点 的右边 有定义,如果极限 存在并且有限,称这个极限值为 在点 的右导数,记作 并称函数 在 点右可导。类似可定义左导数
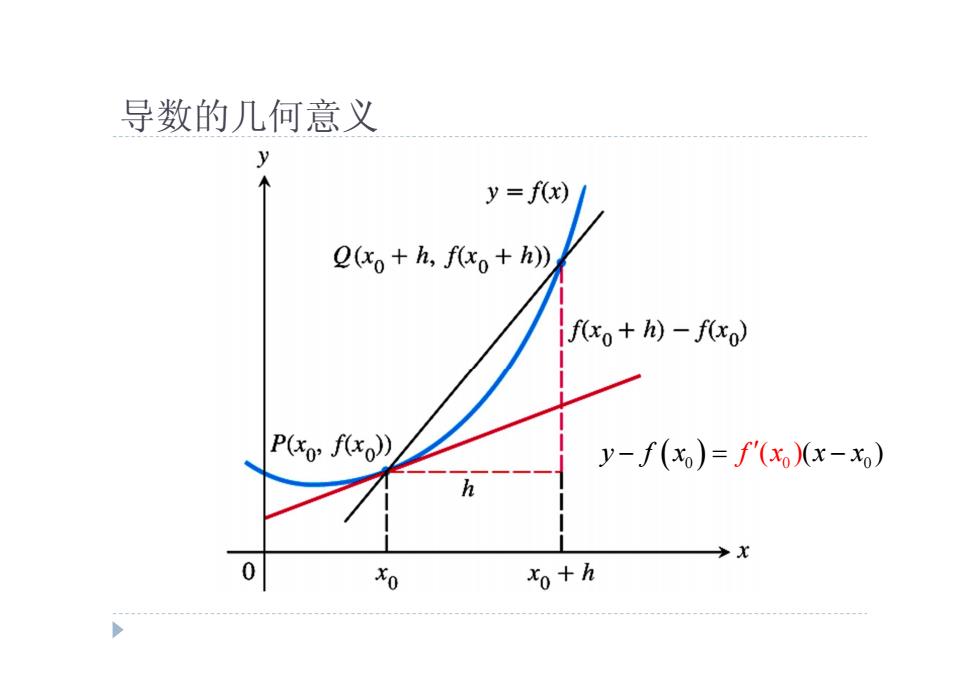
导数的几何意义 y y=f(x) xo+h,fxo+h)) if(xo+h)-f(xo) P(xo:f()) y-f(xo)=f(xo)(x-xo) h 0 0 xo+h
导数的几何意义 0 0 0 y f x x x f x ( )( )

切线 如果函数f:E→R定义在集合EcR且在点x∈E处可导,那么方程 y-f(xo)=f(xo)(x-xo) 给出的直线就叫做这个函数图像在点(x,f(x)的切线
切线 0 0 0 0 0 0 ( )( ) : ( , ( )) y f x f f E E x E x f x x x x 如果函数 定义在集合 且在点 处可导,那么方程 给出的直线就叫做这个函数图像在点 的切线
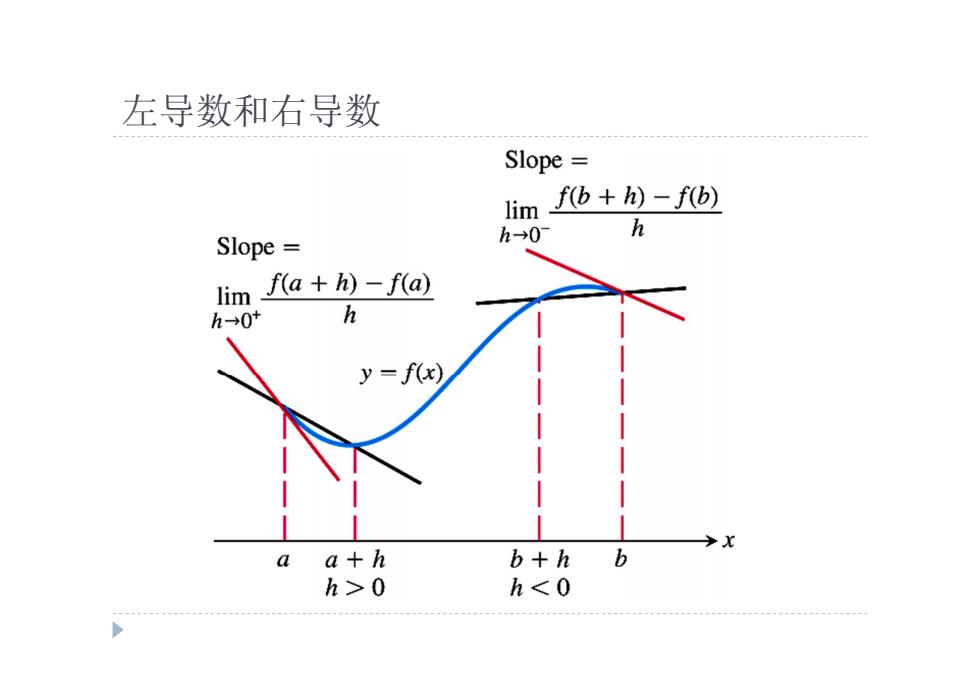
左导数和右导数 Slope= limbh)-f(b) h→0 h Slope= lim fa+h)-f(a) h→0* h y=f(x) aa+h b+h b h>0 h<0
左导数和右导数

例 (x)=ax-,a∈R,(00,a≠l,x∈R) (o.)-zhg(-Oazwaz) (sinx)'=cosx,(cosx)=-sinx
例 1 , , 0 ln , 0, 1, 1 log , 0, 0, 1 ln sin cos , cos sin x x a x x x a a a a a x x x a a x a x x x x

例 1、考察f(x)=x在x=0处的可导性 .1 2、考察函数f(x)= xsin,x≠0 x=0处的连续性和可导性 0, x=0 3、设函数f:(0,+o)→R在x=1处可导,且 f(xy)=f(x)+f(y),x,y∈(0,+o) 证明f在0,+∞处处可导,并且旷(=C田+f0
例 1 ( ) 0 、考察f x x x 在 处的可导性 1 sin , 0 2 ( ) 0 0, 0 x x f x x x x 、考察函数 在 处的连续性和可导性 3 : (0, ) 1 ( ) ( ) ( ), , (0, ) ( ) (0, ) ( ) (1) f x f xy yf x xf y x y f x f f x f x 、设函数 在 处可导,且 证明 在 处处可导,并且

例 奇函数的导函数为偶函数 ,偶函数的导函数为奇函数 周期函数的导函数还是周期函数
例 奇函数的导函数为偶函数 偶函数的导函数为奇函数 周期函数的导函数还是周期函数