北京化工大学：《微积分》课程授课教案（专题讲稿）工科数学分析专题——多变量函数的微分学

多变量函数的微分学

多变量函数的微分学

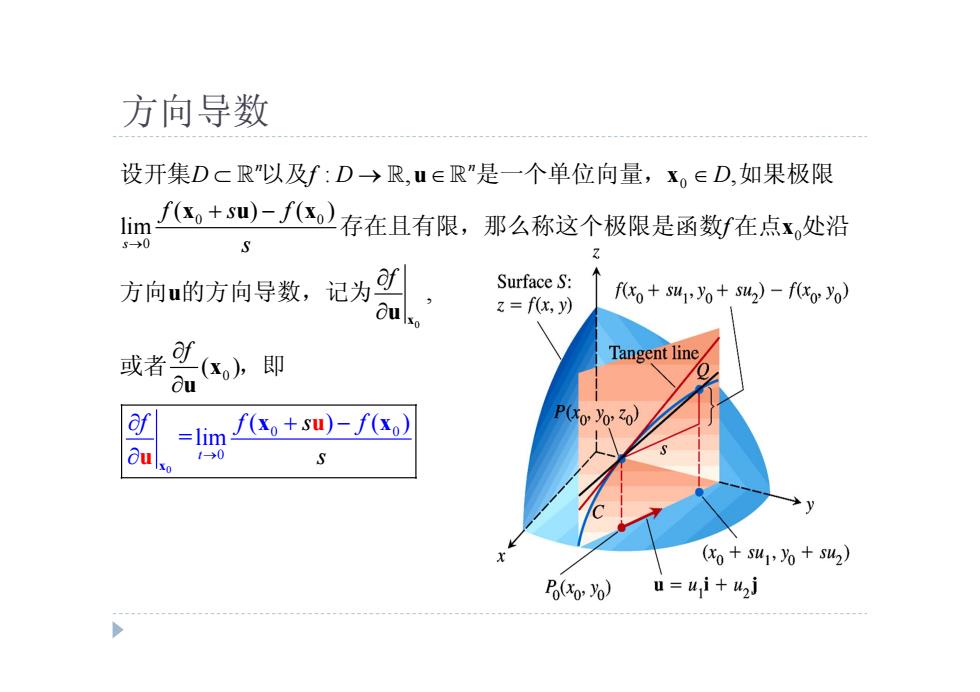
方向导数 设开集DcR"以及f:D→R,u∈R"是一个单位向量，X。∈D,如果极限 m。十0-存在且有限，那么称这个极限是函数在点x处沿 Z 方向u的方向导数，记为 Surface S: z=f(x,y) f(xo+su,yo+su2)-f(xo yo) 或者斗（K,h即 Tangent line Ou f(K+s四)-f(Ko) Pto%,0） =lim 1-→0 S (o+Su1,%+Su2) P(o)u=ui+uzj

方向导数 0 0 0 0 0 0 0 0 0 0 0 : , , ( ) ( ( ) li ) ( ) = m m ) li , ( n n s t D f D D f s f f s f f s s f f f                 x x u u u x x u x x u u x u x x 设开集    以及 是一个单位向量， 如果极限 存在且有限，那么称这个极限是函数 在点 处沿 方向 的方向导数，记为 或者 ，即

例（沿某一方向的方向导数存在但不连续） f(x,y)= 器0 1, (xy)=0 取方向u=(cos0,sin0),f0+u)=sin20=454→1=f(0),其他方向 不连续 计彩方个号国-- 的方向导数存在，f八lo00=0

例（沿某一方向的方向导数存在但不连续）     2 2 2 , , 0 ( , ) 1, , 0 xy x y f x y x y x y          (0 / 4,5 / 4 ,0) =(cos ,sin ) ( )=sin 2 1 ( ) , , 0 f t f f                           取方向u 0 u 0 ， ，其他方向 不连续 2 2 2 2 计算得沿方向 或 的方向导数存在， 2 2 2 2

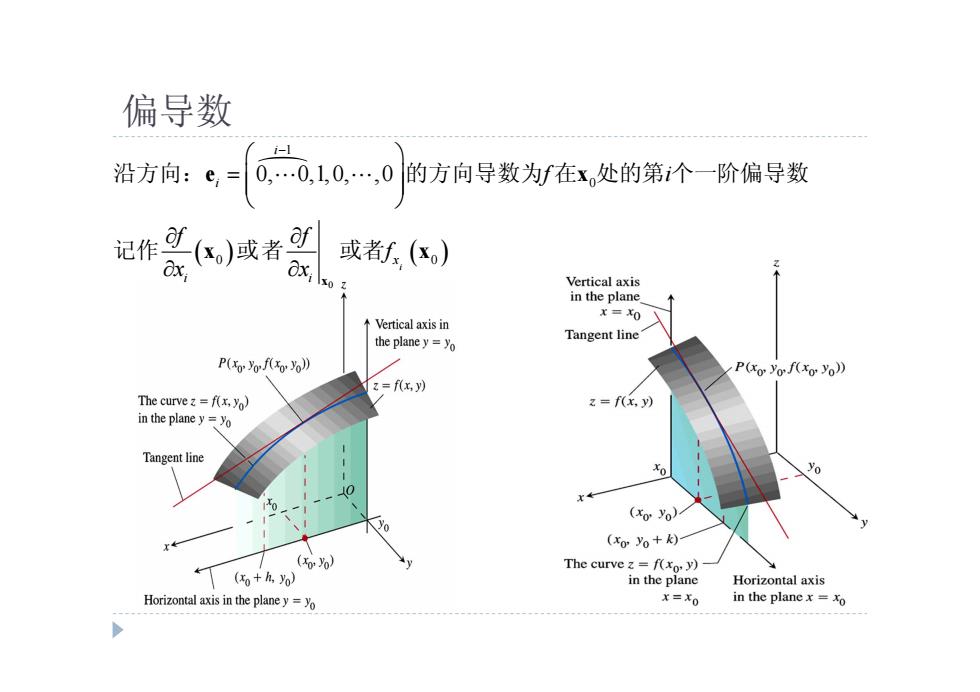
偏导数 沿方向：e,= 0,0,10,…,0的方向导数为f在x处的第个一阶偏导数 记作可，)或者 或者f() Ox, Vertical axis in the plane x=X0 个Vertical axis in the planey=o Tangent line P(o》 P(oof(xor o)) z=f(x,y) The curvez=f(x.Yo) z=f(x,y) in the plane y=yo Tangent line 0 t (xo yo) (xo%+) (o+h,yo) The curve z=f(xo.y) in the plane Horizontal axis Horizontal axis in the plane yo x=x0 in the plane x xo

偏导数      0 1 0 0 0 0, 0,1,0, ,0 i i i x i i f i f f f x x             x e x x x 沿方向：   的方向导数为 在 处的第 个一阶偏导数 记作 或者 或者

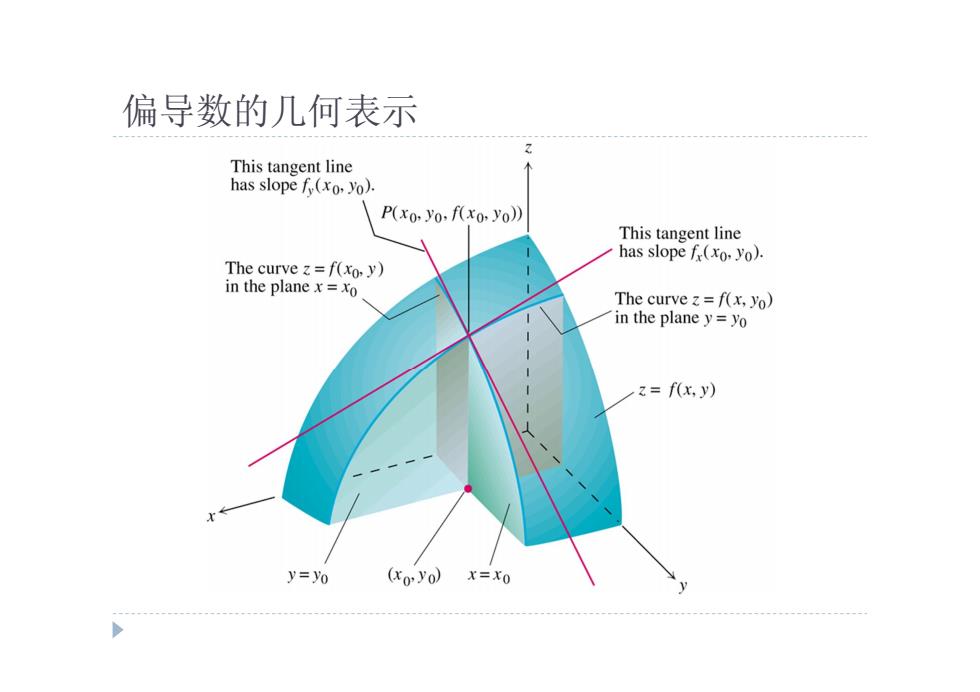
偏导数的几何表示 This tangent line has slope f(xo,yo). P(xo.yo.f(xo.yo)) This tangent line has slope f(xo.yo). The curve z=f(xo.y) in the plane x=xo The curve z=f(x,yo) in the plane y=yo z=f(x,y) y=yo (xoyo)x=xo

偏导数的几何表示

例 1、计算函数x水)=x+y+c0s0y2s)=N,x≠0,2y y+cosx 的各个方向的偏导数 2、计算函数f(x,y)=x2+3xy+y-1在点(4，-5)的偏导数值 3、若方程-n:=x+定义：为x的函数并且偏导数存在，求产 4、平面x=1交抛物面z=x2+y成一抛物线，求此抛物线在(L,2,5)的斜率 5、R,R和R,欧姆的电阻并联成R欧姆的电阻，的值可以从公式 1-上+1+1求出，求R=30,R,=45和R=90欧姆时的 OR RRR R3 Rz

例 2 2 2 1 ( , , ) cos( ) ( ) , 0 cos y f x y z x y y z f y x       、计算函数 ， x x x , 的各个方向的偏导数 2 2、计算函数f x y x xy y ( , ) 3 1 (4, 5)      在点 的偏导数值 3 ln , z yz z x y z x y x      、若方程 定义 为 的函数并且偏导数存在，求 2 2 4 1 (1,2,5) 、平面x z x y    交抛物面 成一抛物线，求此抛物线在 的斜率 1 2 3 1 2 3 1 2 3 2 5 , 1 1 1 1 =30, =45 =90 R R R R R R R R R R R R R R      、 和 欧姆的电阻并联成 欧姆的电阻， 的值可以从公式 求出，求 和 欧姆时的

多变量函数的全微分 设开集DcR"以及f:D→R,取定x∈D,△x=(△x,△x2,…,△x)∈R”, △x=x-x,如果存在一个线性函数L(Ax)=∑L,(K)△x使得 f(xo+Ax)-f(xo)=L(Ax)+o(JAxl) L与△x无关，只与x,有关，则称函数f在x,可微，而△x的一次式L(△x) 称为f在x,的全微分，记作d(,b即d(x,)=∑L,(,)dk 如果f在D的每一点都可微，称f是D上的可微函数

多变量函数的全微分           0 1 2 0 1 0 0 0 0 0 0 0 1 ( : , , , o ) ( , ( ) ) ( ) + ) ) i n i i n n n n i i i i i i D f D D x x x x df x x x f f L L L f df L dx                             0 0 x x x x x x x x x x x x x x x L L x x x 设开集     以及 ，取定 ， ,如果存在一个线性函数 = 使得 与 无关，只与 有关，则称函数f在 可微，而 的一次式 称为 在 的全微分，记作 ( ，即 ( 如果f D f D 在 的每一点都可微，称 是 上的可微函数

一元向量值函数的导数 设f:U(xo)cR→Rm,x,+△xeU(x),若lim f(飞，+△x-f(】存在，则称在 r→0 △x 处可号.记化)减 或Df(x),E 即f'(xo)=lim f(x+△x)-f(x) △r-→0 x=X0 △x sin 2x 例：f(x)= ln(x+V1+x2),求f'(x),f"(x,f"(0) arctanx

一元向量值函数的导数         0 0 0 0 0 0 0 0 0 0 0 0 0 0 ( )= lim : ( ) , ( ), lim ( ) ( ) m x x x x x x x x x x x U x x x U x x d x x D x dx x                   f   f f f f f f f f f 设   若 存在，则称 在 处可导，记为 或 或 ，即 2 sin 2 ( ) ln( 1 ) , ( ), ( ), (0) arctan x x x x x x x                 例：f f f f 求

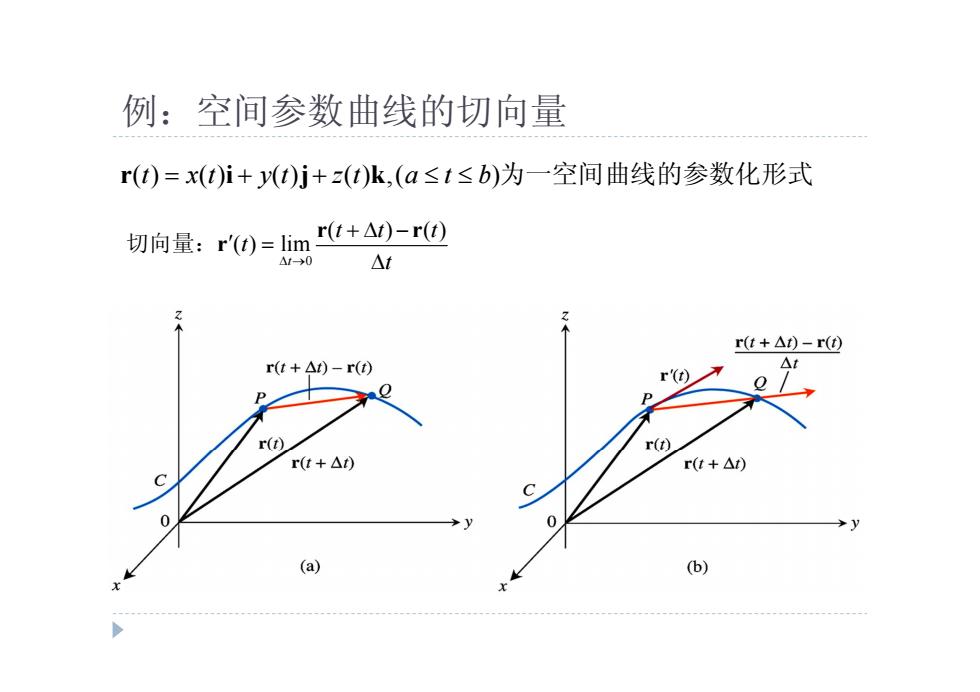
例：空间参数曲线的切向量 r(t)=x(ti+y(t)j+z(t)k,(a≤t≤b)为一空间曲线的参数化形式 切向量：r'(t)=lim r(t+△t)-r(t) △0 △t r(t+△)-r(@ r(t+△)-r() '() At 力 r(t) r() r(t+△) r(t+△) C 0 0 >y (a) (b)

例：空间参数曲线的切向量 r i j k ( ) ( ) ( ) ( ) ,( ) t x t y t z t a t b      为一空间曲线的参数化形式 0 ( ) ( ) ( ) lim t t t t t t         r r 切向量：r

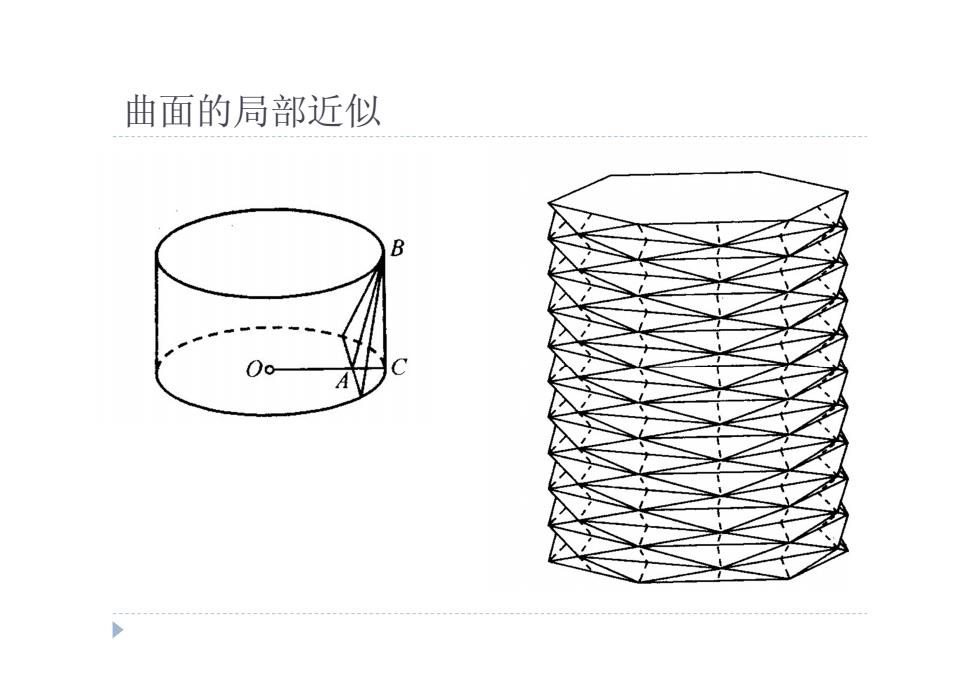
曲面的局部近似 B

曲面的局部近似