
《线性代数》第一章习题解答 1.确定下列排列的逆序数,并指出它们是奇排列还是偶排列. (1)41253 (2)654321(3)nn-1(n-2)…321 解:(1)x(41253)=4偶排列 (2)t(654321)=15奇排列 (3)nn-1)…32.)=nn-1) 当n=4织或4织+1时: 偶排列 当n=4织+2或4明+3时,奇排列. -1325 2只? 706 9 ,试求:A4A2,A2 16231419 1270 解:A4=(-1)-4311=908 162314 -125 42=(-12*2-4119=-803 161419 -125 42=(-1)2*31206=-660 161419 124 -1 3设四阶行列式!11 1 ,试求:A41+A2+A+A4 -256 8 31-5-2 1124-1 1111 解:A1+A2+A3+A4= -2568 =0 1111
-1- 《线性代数》第一章习题解答 1.确定下列排列的逆序数,并指出它们是奇排列还是偶排列. (1)41253 (2)654321 (3) n n n ( 1)( 2) 3 2 1 − − 解:(1) (41253) 4 = 偶排列 (2) (654321) 15 = 奇排列 (3) 1 2 ( ( 1) 3 2 1) ( 1) n n n n − = − , 当 n = + 4 4 1 或 时: 偶排列 当 n = + + 4 2 4 3 或 时,奇排列. 2.设四阶行列式 1 3 2 5 12 7 0 6 4 3 11 9 16 23 14 19 − − ,试求: 14 22 32 A A A , , . 解: 1 4 14 12 7 0 ( 1) 4 3 11 908 16 23 14 A + = − − = , 2 2 22 1 2 5 ( 1) 4 11 9 803 16 14 19 A + − = − − = − , 2 3 32 1 2 5 ( 1) 12 0 6 660 16 14 19 A + − = − = − 3.设四阶行列式 1 2 4 1 1 1 1 1 2 5 6 8 3 1 5 2 − − − − ,试求: 41 42 43 44 A A A A + + + . 解: 41 42 43 44 1 2 4 1 1 1 1 1 0 2 5 6 8 1 1 1 1 A A A A − + + + = = −

4.计算下列行列式: 1352 a12 (1)423 (2) 09 0 -124 0 -2 1 0 0 0 0 (3) 03 2 -1 (3) 0 0 02 4-10 -3 0 a 12 -6 a a 1 0 0 0 a b -1b 1 0 a (5) 0 1 (6) c b a 0 0 0 -1 a b a 1+x 1 1 1 1 1 (7) 1-x 1 11+y 1 1 1 1-川 解:(1)-69(2)-a142241 (3)0(4)a14a202a41 (5)abcd+ab+cd+ad+1 (6)b(b2-4a2)(7)x'y2 5.证明: la? ab b2 (1)2aa+b2b=(a-b) 111 ax+by ay+bz az+bx x y (2)ay+bz az+bx ax+by =(a+b)y =x az+bx ax+by ay+bz x y a2(a+1)2(a+2)2(a+3) (3) 62(b+1)2(b+2)2(b+3) c2(c+1)2(c+2)}2(c+3) =0 d2(d+1)2(d+2)2(d+3)2
-2- 4.计算下列行列式: (1) 3 5 2 4 2 3 −1 2 4 (2) 11 12 13 21 22 31 0 0 0 a a a a a a (3) 1 2 1 0 0 3 2 1 4 1 0 3 1 2 6 3 − − − − − − (3) 14 23 24 32 33 34 41 42 43 44 0 0 0 0 0 0 a a a a a a a a a a (5) 1 0 0 1 1 0 0 1 1 0 0 1 a b c d − − − (6) 0 0 0 0 a b a a a b b a a a b a (7) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 x x y y + − + − 解:(1)-69 (2) −a a a 13 22 31 (3)0 (4) a a a a 14 23 32 41 (5) abcd ab cd ad + + + +1 (6) 2 2 2 b b a ( 4 ) − (7) 2 2 x y 5.证明: (1) 2 2 3 2 2 ( ) 1 1 1 a ab b a a b b a b + = − (2) 3 3 ( ) ax by ay bz az bx x y z ay bz az bx ax by a b y z x az bx ax by ay bz z x y + + + + + + = + + + + (3) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ( 1) ( 2) ( 3) ( 1) ( 2) ( 3) 0 ( 1) ( 2) ( 3) ( 1) ( 2) ( 3) a a a a b b b b c c c c d d d d + + + + + + = + + + + + +

(4) 1 11 1 b cd b2 d =(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)(a+b+c+d) a b c d 解:证明略。 x y 6. 已知 02 3=1, 求下列各行列式的值 11 x-1y-1-1 (1)02 3 (2)13 4 111 11 1 x y (3)3x3y+43z+6 x+1y+12+1 (2)1(3)2 a1a2a3…am a21a2a23… 42m 7.n阶行列式D=a1 dn a3g… di 中,若 … … … … aan2an3…am a,=-anij=1,2,…,n那么称Dn为反对称行列式(n阶) 证明:奇数阶反对称行列式等于零. 明 a1a21a31…an -012 -a13 a12a2a2…an2 -022 -a23 … -02m Dh=a3a23a…an -as -a32 -a3 … … … … … … aa2na3…am-a1 -0n2 -d,m =(-1)Dn=(-1)2Dn=-Dn,∴Dn=0
-3- (4) 2 2 2 2 4 4 4 4 1 1 1 1 ( )( )( )( )( )( )( ) a b c d a b a c a d b c b d c d a b c d a b c d a b c d = − − − − − − + + + 解:证明略. 6.已知: 0 2 3 1 1 1 1 x y z = ,求下列各行列式的值. (1) 1 1 1 3 3 3 0 2 3 1 1 1 x y z (2) 1 1 1 1 3 4 1 1 1 x y z − − − (3) 3 3 4 3 6 1 1 1 x y z x y z x y z + + + + + 解:(1) 1 3 (2)1 (3)2 7. n 阶行列式 11 12 13 1 21 22 23 2 31 32 33 3 1 2 3 n n n n n n n nn a a a a a a a a D a a a a a a a a = 中, 若: , 1, 2, , a a i j n ij ji = − = 那么称 Dn 为反对称行列式( n 阶). 证明:奇数阶反对称行列式等于零. 证明: 11 21 31 1 11 12 13 1 12 22 32 2 21 22 23 2 1 13 23 33 3 31 32 33 3 1 2 3 1 2 3 n n n n n n n n n n nn n n n nn a a a a a a a a a a a a a a a a D a a a a a a a a a a a a a a a a − − − − − − − − = = − − − − − − − − 2 1 ( 1) ( 1) n D D D n n n + = − = − = − , 0 = D n

8.计算n阶行列式 100…01 1010… 0 0 … 2 0 0 0 … 0 (1) 人 (2 … n-1 … 0 0 … 0 … 0 0 n 0 0 … 0 y…00 0x·0 x-m X2 … 0 Xw X2-m (3) ……… (4) … X. 0 … …x y 0 Xa-m … 0 /1 3 … n-1 n 1 1 0 … 0 (5) 2 2 0 o … … … 0 0 n-1 1-n川 1+a 1 1 1 1+a2 1 (6) 1 1+a … … 1 …1+a a 11… a0 … 0 (7) 1 0 0 (aa2…an≠0) ……… 100… (2)(-1)nl
-4- 8. 计算 n 阶行列式 (1) 0 0 0 1 0 0 2 0 0 1 0 0 0 0 0 n n − (2) 0 1 0 0 0 0 2 0 0 0 0 1 0 0 0 n n − (3) 0 0 0 0 0 0 0 0 0 x y x x y y x (4) 1 2 1 2 1 2 n n n m x m x x x x m x x x x − − − (5) 1 2 3 1 1 1 0 0 0 0 2 2 0 0 0 0 0 1 1 n n n n − − − − − (6) 1 2 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 n a a a a + + + + (7) 0 1 2 1 1 1 1 1 0 0 1 0 0 1 0 0 n a a a a − ( a a a 1 2 n 0 ) 解: (1) ( 3) 2 ( 1) ! n n n + − (2) 1 ( 1) ! n n + −

(3)x+(-)“y(4)(←m)一(∑x-m)(各列加到第一列) )(-y子a+(各列如到第一列 1+a1 11+a 1 …1 (6)D.= 11+a2…1 11+a2…1 + …… 0 0…an 1 11 a10…0l =aD-1+ 0a3…0 =anDn-1+a42…an- ………… 11.1 =an[an-Dn-2+a,a2…an-2]+a,a2…an-l =…=a0…aa+a03a.+…+a%a-24.+a4aa =1a1+2马) a (仞44aa.a,-(各列乘-加到第一列1≤15n-D a 9.证明 (1) x-10…0 01 …0 0 …… … =x"+ax-+a2x-2+…+an-x+a。 000 …x -1 a a-an2 …a2x+a cosa 1 0 …0 0 1 2cosa 1 …0 0 (2) 0 1 2cosa… 0 0 cos(na) …… 0 0 … 1
-5- (3) 1 ( 1) n n n x y + + − (4) 1 1 ( ) ( ) n n i i m x m − = − − (各列加到第一列) (5) 1 ( 1) ( 1)! 2 n − + n (各列加到第一列) (6) 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 n n a a a a D a + + + + = + 1 2 1 1 1 2 1 0 0 0 0 1 1 1 n n n n n a a = + = + a D a D a a a − − − 1 2 1 2 2 1 2 1 [ ] = + + a a D a a a a a a n n n n n − − − − = = + + + + a a a a a a a a a a a a a a n n n n n n − − − 1 2 1 2 3 1 2 2 1 2 1 1 1 1 (1 ) n n i i i i a = = a = + (7) 1 1 2 1 0 1 1 ( ) n n n i i a a a a a a − − = − (各列乘 1 i a − 加到第一列 1 1 − i n ) 9. 证明: (1) 1 2 1 2 1 1 2 2 1 1 0 0 0 0 1 0 0 0 0 0 1 n n n n n n n n x x x a x a x a x a x a a a a x a − − − − − − − = + + + + + − + (2) cos 1 0 0 0 1 2 cos 1 0 0 0 1 2 cos 0 0 cos( ) 0 0 0 1 2 cos n =

a1+xa2a3… an-l 0 … 0 0 (3) 0 … 0 0 … … … =…x0+受这里 0 0 X-1 0 0 0 0… -Xn-1 x1x2x3…xn≠0 a+b ab 0 …0 0 a+b ab .0 0 (4) 0 1 a+b…0 0 a-b -(a≠b) 0 0 0 …1a+bl 证明: x -1 0 0 0 0 1 … 0 0 (1)左C-1+xCa… … … … 00 0 … 0 -1 da-l d-2 …x2+ax+a2x+a1 0 -10…00 0 0-1…00 C+xCC+xC … …………… 00…0-1 k+2a,x…………x+a =(-1(x+∑a,x)-(-l1)=+ax++ax+x=右 (2)当n=1时成立,设当n=k时成立,则当n=k+1时,行列式按 第k+1行展开
-6- (3) 1 2 3 1 1 2 2 3 1 1 1 1 0 0 0 0 0 0 (1 ) 0 0 0 0 0 0 0 n n n i n i i n n n a x a a a a x x x x a x x x x x x − = − − + − − = + − ,这里 1 2 3 0 n x x x x . (4) 1 1 0 0 0 1 0 0 0 1 0 0 ( ) 0 0 0 1 n n a b ab a b ab a b a b a b a b a b + + + + − + = − + 证明: (1)左 1 2 1 2 1 2 1 1 0 0 0 0 1 0 0 0 0 0 0 1 n n n n n x x C xC a a a x a x a x a − − − − − + − + + + 2 1 1 2 1 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 n n n n i n i i C xC C xC x a x x a − − − = − − + + − + + 1 1 1 ( 1) ( ) ( 1) n n n n i n i i x a x + − − = = − + − 1 1 1 n n n x a x a x x − = + + + + − =右 (2)当 n =1 时成立, 设当 n k = 时成立,则当 n k = +1 时,行列式按 第 k +1 行展开

lcosθ 1 0 1 2cos0 0 Dm1=2cos0.Dm-… … … 2cos0 0 1 1 =2cos0.D-D-=2cos0.coske-cos(k-1)0=cos(k+1)0 故命题成立 (3) -110…00 左备提出国子≤j≤m)(3名…X,) 0 -11…00 …………… 000…10 0 00…-11 1+ 1 0 0 C+C2+…+Cn)x1x2…xn) … 0 -1 1 0 … … …… 0 00…1 =(出…x1+2=右 a 0 0 … 0 0 1 a+b ab … 0 0 (4) 左=D= 0 0 a+b ab 10 0 0 … a+b b ab 0… 0 0 a+b 名 … 0 0 0 0 0 … a+b ab 0 0 … 1 a+b
-7- 1 cos 1 0 1 2 cos 0 2 cos 2 cos 0 1 1 D D + = − = − = − − = + 2cos 2cos cos cos( 1) cos( 1) D D k k k −1 故命题成立. (3). 1 2 3 1 1 2 3 1 1 2 1 1 1 0 0 0 0 1 1 0 0 (1 ) ( ) 0 0 0 1 0 0 0 0 1 1 n n n n a a a a a x x x x x n j n x x x − − + − − − 左各列提出因子 j 2 3 2 3 1 1 2 1 2 1 0 1 0 0 )( ) 0 1 1 0 0 0 0 1 i n i n n a a a a x x x x i C C C x x x n n = + + + + − 1 2 1 ( )(1 )i i n a n x i x x x = = + =右 (4) 0 0 0 0 1 0 0 0 0 0 0 0 0 1 n a a b ab D a b ab a b + = = + + + 左 0 0 0 1 0 0 0 0 0 0 0 0 1 b ab a b ab a b ab a b + + +
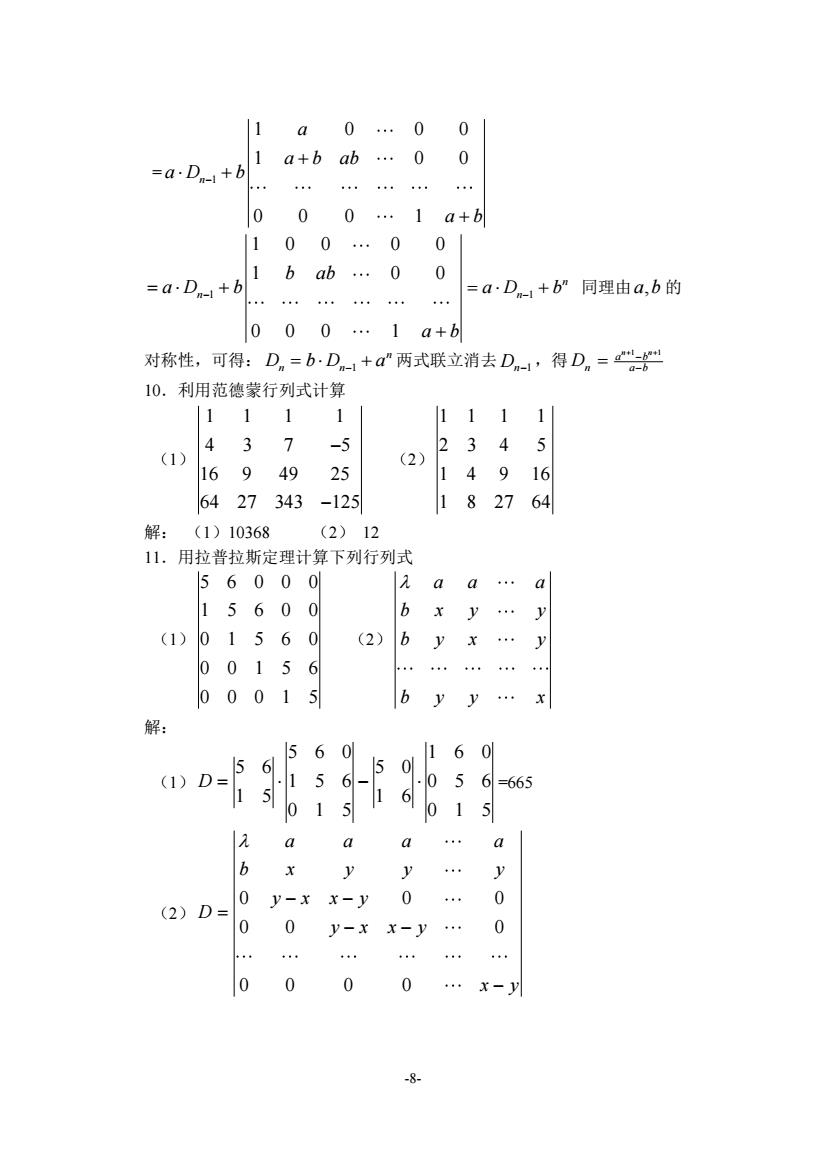
11a 0…00 -a-D+ba+6b…0 0 ……… … 000.1a+b 100…00 =aDn+b16ab… 0 =a·Dn1+b”同理由a,b的 ………… 000…1a+b 对称性,可得:D=b-D1+d两式联立消去Dn1,得Dn=2一 10.利用范德蒙行列式计算 1111 1111 437 (1) (2) 2345 16949 25 14916 6427343-125 182764 解:(1)10368 (2)12 11.用拉普拉斯定理计算下列行列式 56000 2aa…a 15600 bxy…y (1)01560 (2)byx… 00156 …… 0001 5 byy… x 解: 1)D=56560 5 h 056=665 015 6 015 a b y y … 0 y-x x-y (2)D= 0 0 0 y-x x-y … 0 … … 0 0 0 0 …x-y列
-8- = 1 1 0 0 0 1 0 0 0 0 0 1 n a a b ab a D b a b − + + + 1 1 0 0 0 0 1 0 0 0 0 0 1 n b ab a D b a b = + − + 1 n = + a D b n− 同理由 a b, 的 对称性,可得: 1 n D b D a n n = + − 两式联立消去 Dn−1 ,得 n n 1 1 a b D n a b + + − = − 10.利用范德蒙行列式计算 (1) 1 1 1 1 4 3 7 5 16 9 49 25 64 27 343 125 − − (2) 1 1 1 1 2 3 4 5 1 4 9 16 1 8 27 64 解: (1)10368 (2) 12 11.用拉普拉斯定理计算下列行列式 (1) 5 6 0 0 0 1 5 6 0 0 0 1 5 6 0 0 0 1 5 6 0 0 0 1 5 (2) a a a b x y y b y x y b y y x 解: (1) 5 6 0 1 6 0 5 6 5 0 1 5 6 0 5 6 1 5 1 6 0 1 5 0 1 5 D = − =665 (2) 0 0 0 0 0 0 0 0 0 0 a a a a b x y y y y x x y D y x x y x y − − = − − −

|2(n-1)a a 6 x+(n-2)y y 0 0 x-y 0 0 0 0 x-y… 0 … … … 0 0 0 0 x- x-y 0 0 0 … 0 0 x-y 0 0 0 (n-1)a 0 0 x-y 0 … 0 b x+(n-2)y 0 0 0 x-y… 0 … … … … 0 0 0 x-y =[2x+(n-2)y-(n-1)ab(x-y)-2 12.用克莱姆法则解下列线性方程组 2x1+x2-5x3+x4=8 2x1+5x2-3x3+2x4=3 (1) x-3x2 -6x4=8 (2) -x1-3x2+2x3-x4=-1 2x2-x3+2x4=-5 -3x1+4x3+8x-2x4=-5 x+4x2-7x3+6x4=0 6x1-x2-6x3+4x4=2 解:(1)△=27,△=81,△2=-108,△=-27,△4=27 x=3,x2=-4,x3=-1,x4=1 (2)△=17,41=-34,42=0,4=17,4=85 x1=-2,x2=0,x3=1,x4=5 13.求k的值,使下列方程组有非零解 kx+y+=0 x+-2=0 2x-y+z=0 k11 解:△=1k-1=k2-3k-4=0k=4或k=-1 2-11
-9- ( 1) ( 2) 0 0 0 0 0 0 0 0 0 0 0 0 n a a a a b x n y y y y x y x y x y − + − − = − − 0 0 0 0 0 0 0 0 ( 1) 0 0 0 0 ( 2) 0 0 0 0 0000 x y x y n a x y b x n y x y x y − − − − = + − − − 2 [ ( 2) ( 1) ]( )n x n y n ab x y − = + − − − − 12. 用克莱姆法则解下列线性方程组 (1) 1 2 3 4 1 2 4 2 3 4 1 2 3 4 2 5 8 3 6 8 2 2 5 4 7 6 0 x x x x x x x x x x x x x x + − + = − − = − + = − + − + = (2) 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 2 5 3 2 3 3 2 1 3 4 8 2 5 6 6 4 2 x x x x x x x x x x x x x x x x + − + = − − + − = − − + + − = − − − + = 解:(1) = = = − = − = 27 , 81 , 108 , 27 , 27 1 2 3 4 x x x x 1 2 3 4 = = − = − = 3 , 4 , 1 , 1 (2) 1 2 3 4 = = − = = = 17 , 34 , 0 , 17 , 85 1 2 3 4 x x x x = − = = = 2 , 0 , 1 , 5 13. 求 k 的值,使下列方程组有非零解 0 0 2 0 kx y z x ky z x y z + + = + − = − + = 解: 2 1 1 1 1 3 4 0 4 1. 2 1 1 k = − = − − = = = − k k k k − 或k

x+y+2=1 14.设有方程组 ax+by+cz=d 试求它能用克莱姆法则求解的条 a'x+by+cz=d 件,并求出解。 解 111 △=abc=(b-ac-a)(c-b)a+b+c)≠0 a≠b,a≠c,b≠c,a+b+c≠0时有解,且解为 x-(b-dXc-dXc-b)d+b+c) (b-a)(c-a)(c-b)a+b+c) x,-(d-aXc-aXc-d)d+b+c) (b-a)(c-a)(c-b)(a+b+c) (b-a)(d-a)(d-b)(a+b+c) x3= (b-a)(c-a)(c-b)a+b+c) 111. 1 xa1a2…an- 14.设F(x)=x2a2 a…a,其中a,…an互不相同。 … …… x-laag-…a 请说明F(x)为n-I次多项式,并求出F(x)=0的全部根 解:F)=a-)几(a-a),最高次x前系数为: (-r几(a-a,少,F)-0的全部根为a,=l2…,n-) -10-
-10- 14.设有方程组 3 3 3 3 x y z 1 ax by cz d a x b y c z d + + = + + = + + = 试求它能用克莱姆法则求解的条 件,并求出解. 解: 3 3 3 1 1 1 a b c b a c a c b a b c ( )( )( )( ) 0 a b c = = − − − + + + + a b a c b c a b c , , , 0 时有解,且解为: 1 2 3 ( )( )( )( ) ( )( )( )( ) ( )( )( )( ) ( )( )( )( ) ( )( )( )( ) ( )( )( )( ) b d c d c b d b c x b a c a c b a b c d a c a c d d b c x b a c a c b a b c b a d a d b a b c x b a c a c b a b c − − − + + = − − − + + − − − + + = − − − + + − − − + + = − − − + + 14. 设 1 2 1 2 2 2 2 1 2 1 1 1 1 1 1 2 1 1 1 1 1 ( ) n n n n n n n x a a a F x x a a a x a a a − − − − − − − = ,其中 1 1 , n a a − 互不相同。 请说明 F x( ) 为 n −1 次多项式,并求出 F x( ) 0 = 的全部根. 解: 1 1 1 1 ( ) ( ) ( ) n i i j i j i n F x a x a a − = − = − − , 最高次 n 1 x − 前系数为: 1 1 1 ( 1) ( ) n i j j i n a a − − − − , F x( ) 0 = 的全部根为 ( 1,2, , 1) a i n i = −