
北京化工大学2008一2009学年第二学期 《线性代数(48学时)》考试试卷 班级: 姓名: 学号: 分数: 题号 二 总分 得分 一、填空题(每题4分) 1.设A,B都是四阶方阵,列分块为A=(a,B,B2,月),B=(y,B,B,月),且 |A=1,=2,则A-2=一 2设4-028(引则4- 3.设a=(-3,0,1),B=(0,3,-2)是Ar=0的两个解,其中 (123 A=-1a-3 12 b 则a=,b= 4.实二次型fx,出,x)=x-号+3x的秩为一,正惯性指数为一。 5.设(I),(II)是线性空间V的两个基,(I)到(II)的过渡矩阵为T。若线性变 换o在基(II)下的矩阵为A,则o在基(I)下的矩阵为 第1页
第 1 页 北京化工大学 2008——2009 学年第二学期 《线性代数(48 学时)》考试试卷 班级: 姓名: 学号: 分数: 题号 一 二 三 总分 得分 一、填空题(每题 4 分) 1. 设 A B, 都是四阶方阵,列分块为 A = ( , , , 1 2 3 ) , B = ( , , , 1 2 3 ) ,且 A =1, B = 2 ,则 A B − = 2 。 2.设 A = (1 2 3), 1 1 1 2 3 B = ,则 ( ) 5 T A B = 。 3.设 ( 3,0,1)T = − , (0,3, 2)T = − 是 Ax = 0 的两个解,其中 1 2 3 1 3 1 2 A a b = − − , 则 a = ,b = 。 4. 实二次型 2 2 2 1 2 3 1 2 3 f x x x x x x ( , , ) 3 = − + 的秩为 ,正惯性指数为 。 5. 设(I),(II)是线性空间 V 的两个基,(I)到(II)的过渡矩阵为 T 。若线性变 换 在基(II)下的矩阵为 A ,则 在基(I)下的矩阵为
二、计算题(每题14分) 1.求行列式的值。 a(a-l)”…(a-n) 1a100 P1610 a-(a-l)-…(a-n) (1) 0-1c2) (n≥2)。 o0-1d aa-1…a-n 1 1… 1 第2页
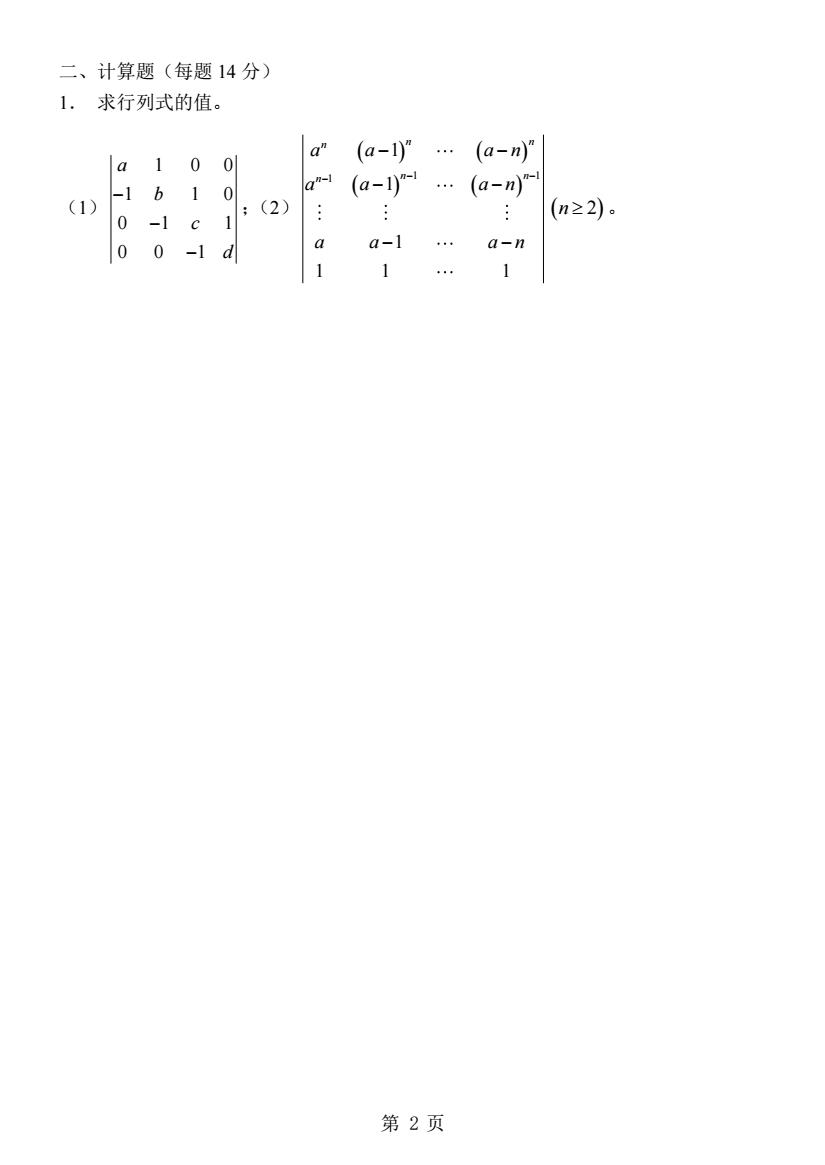
第 2 页 二、计算题(每题 14 分) 1. 求行列式的值。 (1) 1 0 0 1 1 0 0 1 1 0 0 1 a b c d − − − ;(2) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 1 1 1 n n n n n n a a a n a a a n a a a n − − − − − − − − − (n 2)

2.设 2 1= as 449 ()求向量组的秩: (2)求向量组的一个极大线性无关组,并用它线性表示其余向量。 第3页
第 3 页 2.设 1 2 3 4 5 2 1 1 1 2 1 1 2 1 4 , , , , . 4 6 2 2 4 3 6 9 7 9 − − − = = = = = − − − (1) 求向量组的秩; (2) 求向量组的一个极大线性无关组,并用它线性表示其余向量

3.对线性方程组 X-x2-x3+x4=0, x-x2+x3-3x4=1, -%-2%+3现= ()求导出方程组的一个基础解 (2)求方程组的通解。 第4页
第 4 页 3.对线性方程组 1 2 3 4 1 2 3 4 1 2 3 4 0, 3 1, 1 2 3 , 2 x x x x x x x x x x x x − − + = − + − = − − + = − (1) 求导出方程组的一个基础解系; (2) 求方程组的通解

4.设 (400 A=031 013 求一个正交矩阵T,使TAT为对角矩阵,并写出这个对角矩阵。 第5页
第 5 页 4.设 400 0 3 1 0 1 3 A = , 求一个正交矩阵 T ,使 1 T AT − 为对角矩阵,并写出这个对角矩阵

5.设,,是几何向量空间R的一个基,T表示把向量投影到xOy平面的线性变换, 即T(xi+yj+)=xi+yj, (1)求T在基后,万下的矩阵: (2)求T在基(,j,i+j+)下的矩阵。 第7页
第 7 页 5.设 (i j k , , ) 是几何向量空间 3 R 的一个基, T 表示把向量投影到 xOy 平面的线性变换, 即 T xi y j zk xi y j ( + + = + ) , (1)求 T 在基 (i j k , , ) 下的矩阵; (2)求 T 在基 (i j i j k , , + + ) 下的矩阵

三、证明题(10分) 设A是mxn矩阵,m>n。证明:A4=0。 第8页
第 8 页 三、证明题(10 分) 设 A 是 m n 矩阵,m n 。证明: 0 T AA =