
第三章 线性方程组 3.1维向量及其线性运算 3.2 线性相关性 3.3 向量组的秩 3.4 矩阵的秩 3.5 齐次线性方程组 3.6非齐次线性方程组
第三章 线性方程组 3.1 n维向量及其线性运算 3.2 线性相关性 3.3 向量组的秩 3.4 矩阵的秩 3.5 齐次线性方程组 3.6 非齐次线性方程组

第一节n维向量及其运算 定义1: 数域P上的n个有次序的数41,2,,m 所组成的有序数组 称为数域P上的一个 n 维向量(vector),其中心称为第i个分量。 以后我们用小写希腊字母Q,B,Y·来代表向量。 而用小写拉丁字母,b,C,·来代表数
定义1:数域P上的n 个有次序的数 所组成的有序数组 称为数域P上的一个 n 维向量(vector), 其中 称为第 i 个分量。 1 2 , , , n a a a ( ) 1 2 , , , n a a a i a 以后我们用小写希腊字母 , , 来代表向量。 而用小写拉丁字母 a,b,c, 来代表数。 第一节 n 维向量及其运算
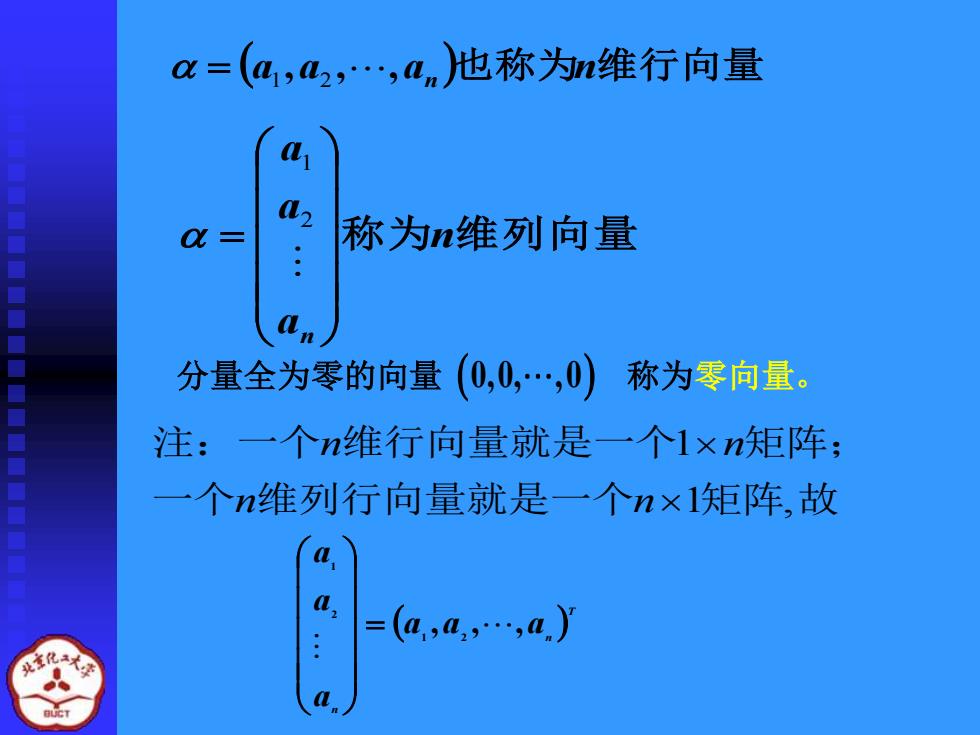
a=(a,a2,,an也称为n维行向量 0 称为n维列向量 分量全为零的向量(0,0,…,0 称为零向量。 注:一个n维行向量就是一个1×n矩阵; 一个n维列行向量就是一个nx1矩阵,故 a =(a,4,,a)
= (a1 ,a2 , ,an )也称为n维行向量 称 为n维列向量 a a a n = 2 1 分量全为零的向量 (0,0, ,0) 称为零向量。 一个 维列行向量就是一个 矩阵 故 注:一个 维行向量就是一个 矩阵; 1 , 1 n n n n ( ) T n n a a a a a a , , , 1 2 2 1 =

例: ()n个未知量的任一齐次线性方程组的每一个 解都是一个每一个解都是一个维向量,且其几 个解的线性组合仍是齐次线性方程组的解。 (2)一个×n矩阵的每一行都是一个n维向量, 而它的每一列都是m维向量;反之,将m个n 维向量按行排列,就可构成一个m×n矩阵。将 n个m维向量按列排列,就可构成一个m×n矩 阵
例: (1) n个未知量的任一齐次线性方程组的每一个 解都是一个每一个解都是一个n维向量,且其几 个解的线性组合仍是齐次线性方程组的解。 (2) 一个 m× n 矩阵的每一行都是一个 n 维向量, 而它的每一列都是 m 维向量;反之,将 m 个 n 维向量按行排列,就可构成一个 m× n 矩阵。将 n个 m 维向量按列排列,就可构成一个m× n 矩 阵

定义2如果a=(a,,…,an)和B=(b,b,,b) 是两个维向量,如果他们的对应分量都相等 即a,=b: (i=1,2,,n),则称向量a和B 相等,记做:a=B。 定义3 如果a=(41,,,an)和B=((亿,b,,b)》 是两个n维向量,则c与B的和a+B为 a+B=(a1+b,a2+b2,…,an+bn) 负向量:向量-C=(一4,一a2,,一am 称为向量的负向量 向量的差:a-B=a+(-β)
定义2 如果 和 是两个 n 维向量,如果他们的对应分量都相等, 即 , 则称向量 和 相等,记做: = 。 ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b 1,2, , ( ) i i a b i n = = 定义3 如果 和 是两个n 维向量,则与的和 + 为: ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b ( , , , ) 1 1 2 2 n n + = a + b a + b a + b 负向量:向量 称为向量的负向量; ( , , , ) 1 2 n − = −a −a −a 向量的差: − = + (−)

数乘运算:设k为数域P中的数,向量 (ka,ka,,ka,)称为向量a=(a,4,,a,) 与数k的数量乘积。记为ka。 数乘运算满足下列四条规则: (1)1ox=c (2)k(la)=(k)a (3)(k+1a=ka+la (4)k(a+B)=ka+kB Q,B是n维向量,k,l∈P
数乘运算:设 k 为数域 P 中的数,向量 ( ) 1 2 , , , n ka ka ka 称为向量 ( ) 1 2 , , , n = a a a 与数 k 的数量乘积。记为 k 。 数乘运算满足下列四条规则: ( ) n k l P k k k k l k l k l k l + = + + = + = = , , (4) ( ) (3) (2) ( ) ( ) (1)1 是 维向量,

加法运算满足性质 (5)a+B=B+a (6(a+)+y=(a+B)+ (7)a+0=c (8)a+(a)=0 注 ·零向量和负向量是唯一的 ·加法的逆运算是减法
(8) ( ) 0 (7) 0 (6)( ) ( ) (5) + − = + = + + = + + + = + 加法运算满足性质 注: • 零向量和负向量是唯一的 •加法的逆运算是减法

线性运算:上述向量的加法及数乘运算称为向量 的线性运算。 注: 满足上述(1)一(8)的运算称为线性运算。 1)0a=0 (2)(-1)a=-C, (3)20=0 (4)如果ka=0,则k=0或a=0
线性运算:上述向量的加法及数乘运算称为向量 的线性运算。 注: •满足上述 (1)–(8) 的运算称为线性运算。 (4) 0, 0 0 (3) 0 0. (1) 0 0 (2) ( 1) ; = = = = = − = − 如果k 则k 或
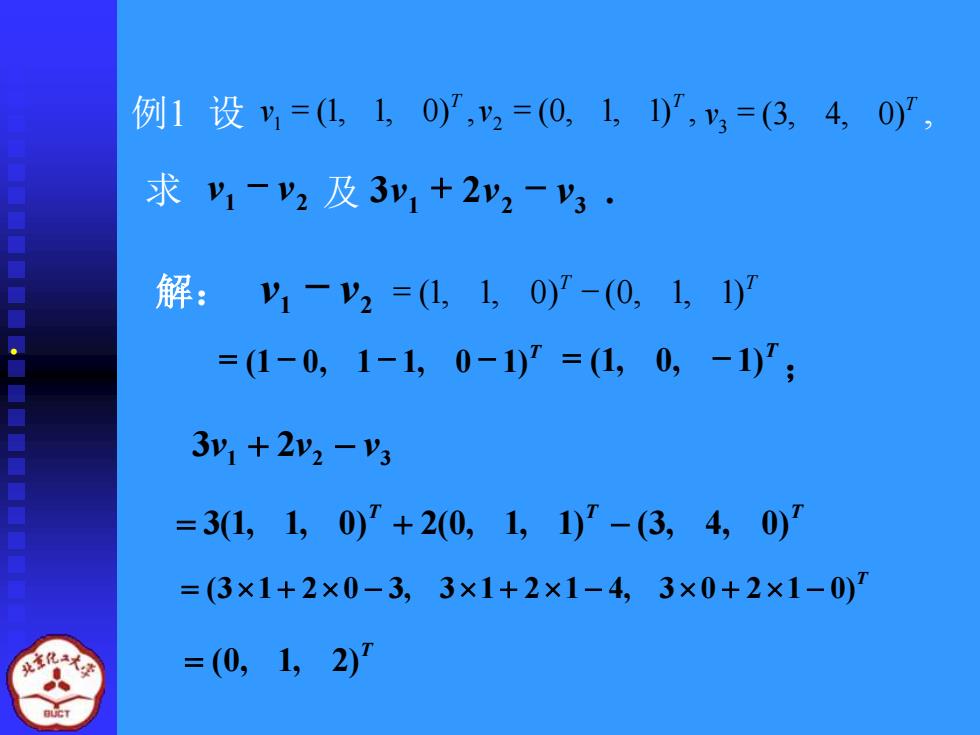
例1设y=(L10),y2=(0,1,1),y3=(3,4,0) 求1-2及3y1+2y2-V· 解:y-y2=(1,10)-(0,1,1) =0-0,1-1,0-1)=(1,0,-1); 3y1+2y2- =31,1,0)+2(0,1,1)'-3,4,0) =(3×1+2×0-3,3×1+2×1-4,3×0+2×1-0) =(0,1,2)1
例1 设 (1, 1, 0) , (0, 1, 1) , 1 2 T T v = v = T v (3, 4, 0) 3 = , 求 1 2 v − v 及 1 2 3 3v + 2v − v . 解: 1 2 v − v T T = (1, 1, 0) − (0, 1, 1) T = (1 − 0, 1 − 1, 0 − 1) T = (1, 0, − 1) ; . 3 1 2 2 3 v + v − v T T T = 3(1, 1, 0) + 2(0, 1, 1) − (3, 4, 0) T = (31 + 2 0 − 3, 31 + 21 − 4, 3 0 + 21 − 0) T = (0, 1, 2)

例2.设3(a1-a)+2(a2+a)=5(a3+a) 其中a1=(2,5,1,3)a2=(10,1,5,10) a3=(4,1,-1,1)7,求a 解:由3(a,-a)+2(a2+a)=5(a3+a 整理得 a=63a+2a-5a =325,13+2101,510-541,-1,1y] =(1,2,3,4)7
例 2.设 3( ) 2( ) 5( ) 1 2 3 a − a + a + a = a + a 其中 T a (2,5,1,3) 1 = , T a (10,1,5,10) 2 = , T a (4,1, 1,1) 3 = − , 求 a 解: 由 3( ) 2( ) 5( ) 1 2 3 a − a + a + a = a + a 整理得 (3 2 5 ) 6 1 a a1 a2 a3 = + − [3(2,5,1,3) 2(10,1,5,10) 5(4,1, 1,1) ] 6 1 T T T = + − − T = (1,2,3,4)