北京化工大学：《线性代数》课程教学资源（PPT课件）第三章 线性方程组 第五节 齐次线性方程组的解法

第五节 齐次线性方程组的解法 ~齐你线性方腥组解的性质 >基础解系及其求法

第五节 齐次线性方程组的解法 ➢ 齐次线性方程组解的性质 ➢基础解系及其求法

,齐次线性方程组解的性质 1。解向量的概念 设有齐次线性方程组 011+0122++a1nXn=0 02131+422少2+…+42mXn=0 (1 0m心1+0m22+…+ann=0 写成矩阵形式为 A4x=0. 其中 A=( 为(1)的系数矩阵

一.齐次线性方程组解的性质 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     （1 写成矩阵形式为 Ax = 0. A (a ) ij mn 其中 = 为（1）的系数矩阵， １．解向量的概念

X= 称为方程组(1)的解向量，亦即方程组(1)的 解。 2,齐次线性方程组解的性质 (1)若x=51,x=52为Ax=0的解，则 x=51+52 也是Ax=0的解， 证明A51=0,A5=0 ∴.A(5+5)=A5+A52=0

              = n x x x x  2 1  A 1 = 0, A 2 = 0 称为方程组（1）的解向量，亦即方程组（1）的 解。 ２．齐次线性方程组解的性质 （1）若 x =  1 ,x =  2 为 Ax = 0 的解，则 x =  1 +  2 也是 Ax = 0 的解. 证明  A( 1 +  2 ) = A 1 + A 2 = 0

故x=5气+52也是Ax=0的解 (2)若x=5为Ax=0的解，k为实数，则 x=k5也是Ax=0的解. 证明A(k5)=kA(5)=k0=0. 证毕

0 . 故 x =1 + 2 也是Ax = 的解 （ 2）若 为 的解， 为实数，则 也是 的解． x =  1 Ax = 0 k x = k 1 Ax = 0 证明 A(k ) kA( ) k 0 0.  1 =  1 = = 证毕

二、 基础解系及其求法 1。基础解系的定义 01,2,…,7,称为齐次线性方程组Ax=0的基础 解系，如果 (1)门1,12，…，1是Ax=0的一组线性无关的解； 如果1,2，，，为齐次线性方程组Ax=0 的一组基础解系，那么，Ax=0的通解可表示为

１．基础解系的定义 二、基础解系及其求法 解系 如果 称为齐次线性方程组 的基础 , h1 ,h 2 ,,h t Ax = 0 (1) , , , 0 ; h 1 h 2  h t是Ax = 的一组线性无关 的解 的一组基础解系 那么 的通解可表示为 如果 为齐次线性方程组 0 = = Ax t Ax , , h1 ,h2 ,,h 0

x=kh1+k22+…+k,n 其中k1,k2,,k,是任意常数 2,线性方程组基础解系的求法 定理 若齐次线性方程组的系数矩阵A的秩 R(A)片<n(未知量的个数)，则(1)必有基础解系： 且基础解系中含有n-r个解向量. 证明 因R(A)戶<n,则A可经有限次初等行变换和列 的换法变换化为B型阵，即

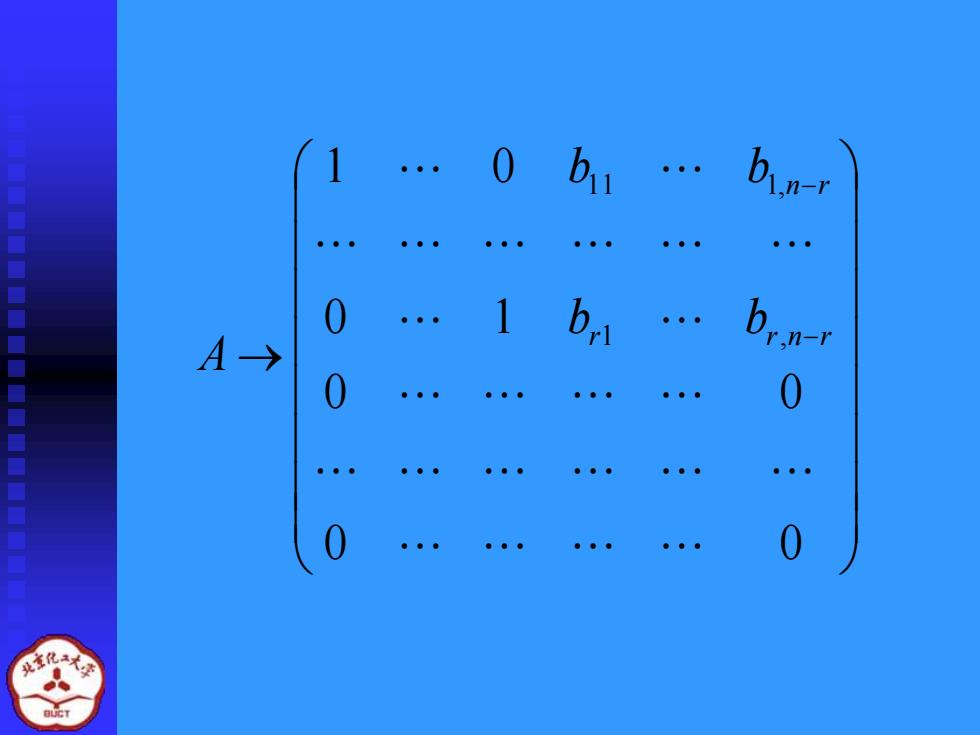
t t x = k1h1 + k2h2 ++ k h , , , . 其中k1 k2  kn−r是任意常数 ２．线性方程组基础解系的求法 定理 若齐次线性方程组的系数矩阵A的秩 R(A)=r<n(未知量的个数），则（1）必有基础解系； 且基础解系中含有n-r个解向量. 证明 因R(A)=r<n,则A可经有限次初等行变换和列 的换法变换化为B型阵,即 ．

0b1…bnr 0 A- r.n-r 0

                    → − − 0 0 0 0 0 1 1 0 1 , 1 1 1,                         r r n r n r b b b b A

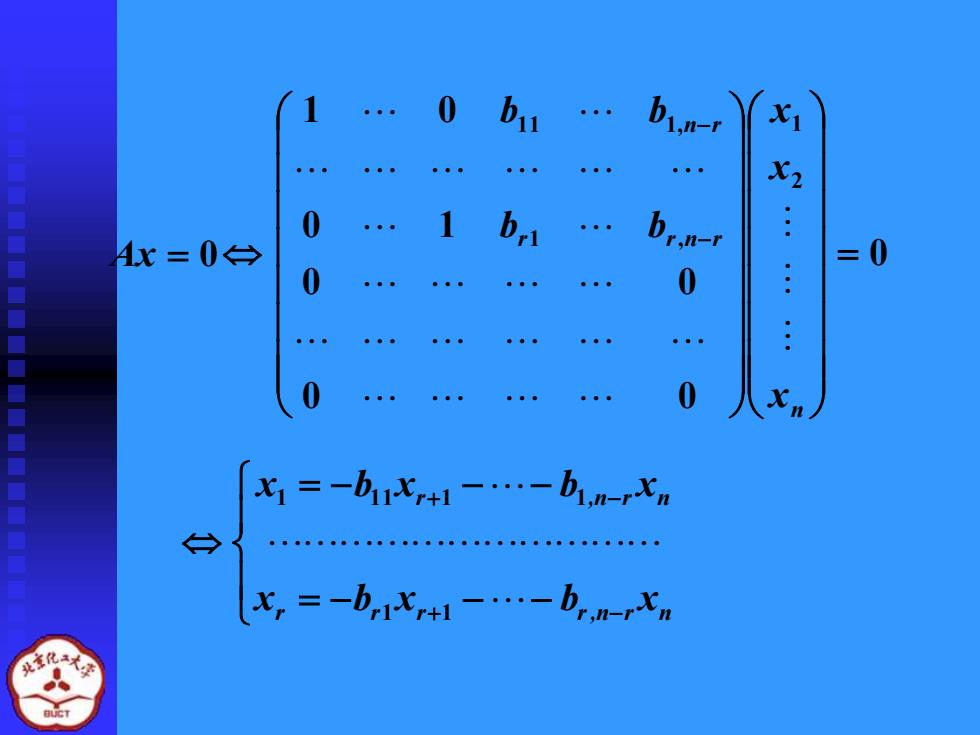
1 bin-r 2 0 b 4x=0台 :.: =0 0 0 0 0 =-b心+1--bn-n x=-b-brn

0 0 0 0 0 0 1 1 0 2 1 1 , 1 1 1, =                                       − − n r r n r n r x x x b b b b                                 = − − − = − − −  + − + − r r r r,n r n r ,n r n x b x b x x b x b x    1 1 1 1 1 1 1 Ax = 0

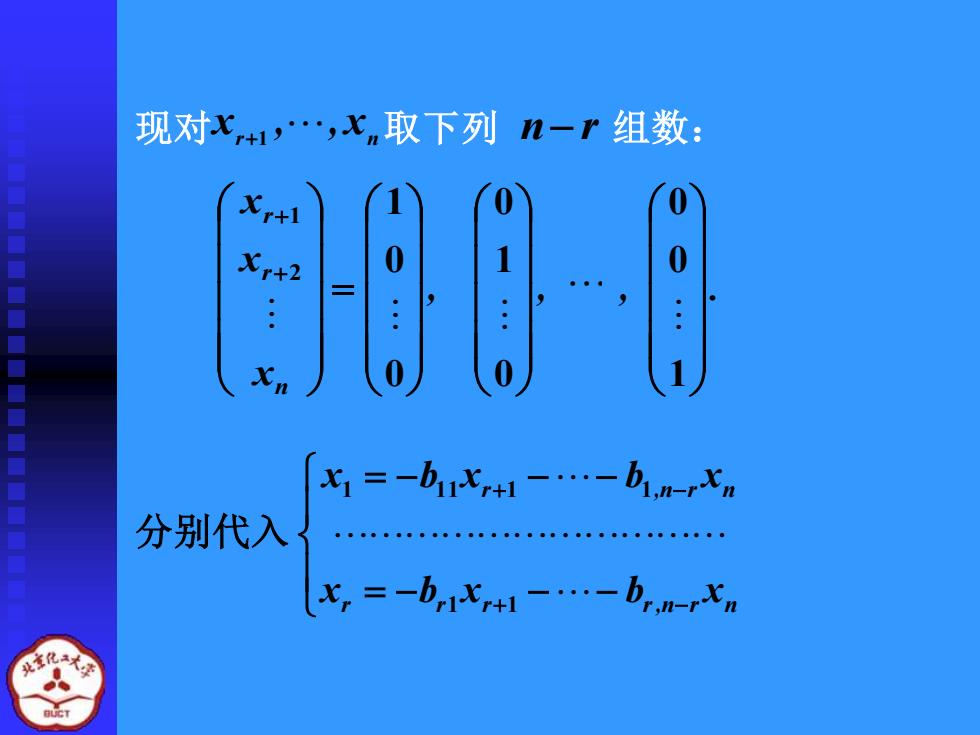
现对x,41,,心n取下列n一r组数： 1=-b1X+1--b1-x2 分别代入 =br1br-rn

现对 x r+1 ,  , x n 取下列 n− r 组数：               + + n r r x x x  2 1      = − − − = − − − + − + − r r r r,n r n r ,n r n x b x b x x b x b x    1 1 1 1 1 1 1 分别代入 , .               1 0 0  ,               0 1 0  ,               = 0 0 1  

依次得 从而求得原方程组的n一P个解： bi b12 bi.n-r b b:2 5 1 52= 0 5- 0 0 0 0

依次得           xr x  1 , b b r                       − − = 0 0 1 1 11 1    , 0 1 0 2 12 2                       − − =   br b  . b b r,n r ,n r n r                       − − = − − − 1 0 0 1    从而求得原方程组的 n− r 个解： . b b , r,n r ,n r           − − − −  1 , b b r           − − 2 12 ,  b b r           − − = 1 11   