
08-09高数(上)期中试题 一、填空3分×27=81分) 1.设f(x)的定义域D=[0,1],f(x-a),(a>0)的 定义域D,=[a,a+1] 0≤x-a≤1, a≤x≤a+1, 2.1g(0+3x)= m(1+3x)=lim+3x)3=e
08-09高数(上)期中试题 1 2 f x D = f x - a a [0,1], ( ),( 0) D = 1.设 ( )的定义域 的 定义域 ( ) 1 0 lim 1 3 x x x → 2. + = 一 、填空(3 27 81 分 = 分) 0 1, − x a a x a+ 1, [ 1] a,a+ ( ) ( ) 1 1 3 3 3 0 0 lim 1 3 lim 1 3 x x x x x x e → → + = + =
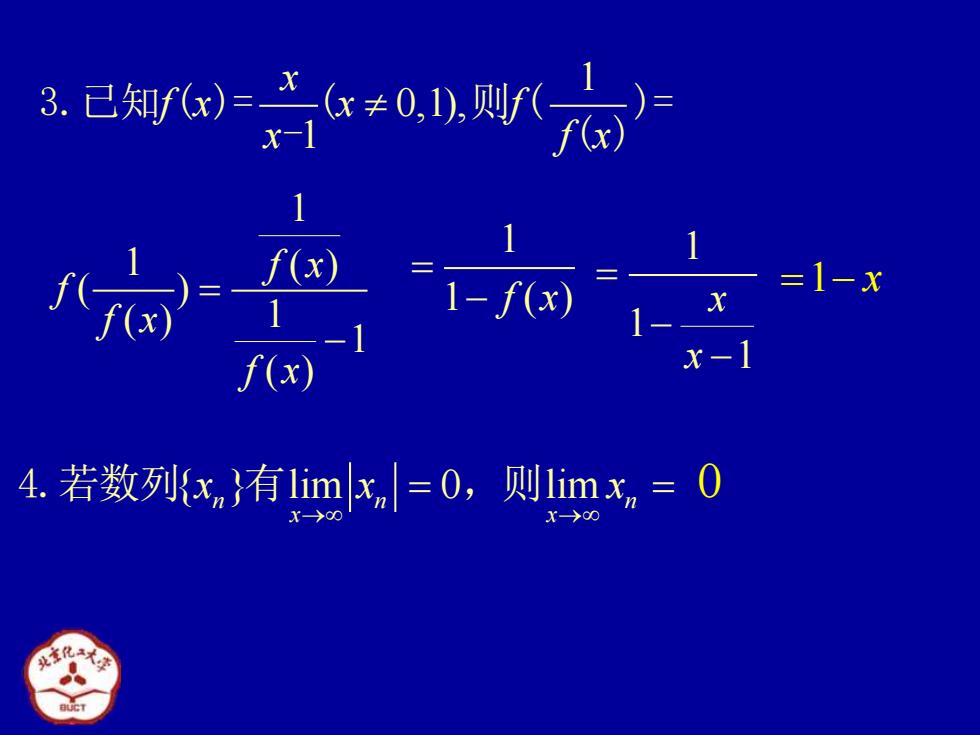
3已w六=7友 f(x) 4.若数列{xn}有1imx=0,则1imxn=0 r-so →00
1 0,1), 1 x f x x f x f x 3.已知 ( )= ( 则 ( )= - ( ) 1 1 ( ) ( ) ( ) 1 1 ( ) f x f f x f x = − 1 1 ( ) f x = − = −1 x 1 1 1 x x = − − { } lim 0 lim n n n x x x x x → → 4.若数列 有 = = ,则 0

5.lim x→+arccotx In lim lim x→+arccotx x→+arc cot x 1 lim 1+x2 =lim x>+∞ x-+o0 =1 1+x2
1 ln 1 5 lim cot x x →+ arc x + . = =1 1 lim cot x x →+ arc x 2 2 1 lim 1 1 x x x →+ − = − + 2 2 1 lim x x →+ x + = 1 ln 1 lim cot x x →+ arc x + =
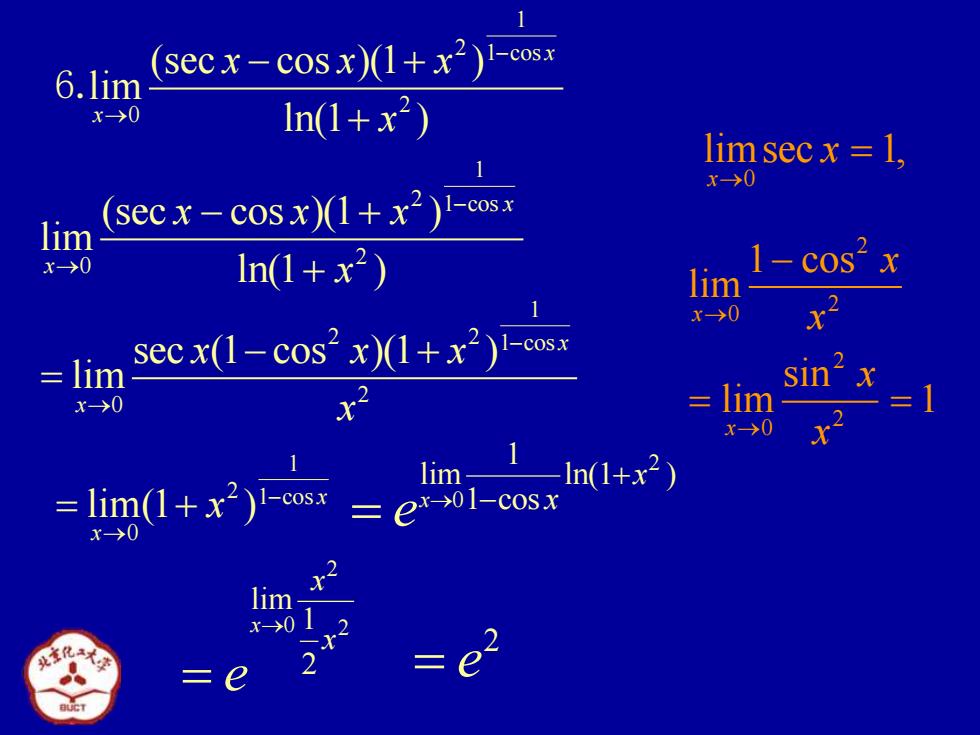
6.lim (secx-cosx)(1+x2)1-cosx x→0 In(1+x2) limsecx =1, x-)0 lim (secx-cosx)(1+x2)1-cosx x-→0 ln(1+x2) lim 1-cosx lim Seex(1-cos'(1+ x→0 x sin2 x x→0 lim =1 =lim1+x2))-eosx lim,In(+x2) =e1w x0 2 lim x-0 =e
1 2 1 cos 2 0 (sec cos )(1 ) lim ln(1 ) x x x x x x − → − + + 6. 2 = e 1 2 2 1 cos 2 0 sec (1 cos )(1 ) lim x x x x x x − → − + = 1 2 1 cos 0 lim(1 ) x x x − → = + 2 0 1 lim ln(1 ) x 1 cos x x e → + − = 2 0 2 lim 1 2 x x x e → = 1 2 1 cos 2 0 (sec cos )(1 ) lim ln(1 ) x x x x x x − → − + + 0 limsec 1, x x → = 2 2 0 2 2 0 1 cos lim sin lim 1 x x x x x x → → − = =

7.若数列x,}满足对Vn,xn>0且lim=a,则a的取值范围 a≥0 8.给间断点分类:点x= 是函数y=X的 间断点 tan x lim* 第一类可去间断点 x→tanx 9.无穷小阶的比较:当x→>0时,f(x)=2+3-2与x 比较是同阶 无穷小 lim 2*+3-2 2-1 +3- x→0 x→0 X xIn 2 lim lim xIn3 =1n2+ln3=1n6 x)0 x→0X
2 tan x x y x 8.给间断点分类:点 = = 是函数 的 间断点 2 lim 0 x tan x x → = { } , 0 lim , n n n n x n x x a a → 7.若数列 满足对 = 且 则 的取值范围 a 0 第一类可去间断点 9 0 ( ) 2 3 2 x x .无穷小阶的比较:当x f x x → = + − 时, 与 比较是 同阶 无穷小 0 0 2 3 2 2 1 3 1 lim lim( ) x x x x x x → → x x x + − − − = + = + = ln 2 ln3 ln6 0 0 ln 2 ln 3 lim lim x x x x → → x x = +

10.曲线y=e在点(0,1)处的切线方程y=x+1 y'=e* y(0)=1当x=0时,y=1 y-1=1(x-0) 山设y+1=e确应妃的函数则密 y+x'=e'y' 当x=0时,y=0 y(0)=0
0 1 , y x dy xy e y x dx + = = = 11.设 确定 是 的函数 则 当x y = = 0 , 0 时 x 10.曲线y e = 在点(0,1)处的切线方程 x y e = y y xy e y + = y (0) 0 = y (0) 1 = 当x y = = 0 , 1 时 y - x = ( − ) y x+ = 1 y y y e x = −

12.设 在t=0处法线方程 2x-y-3=0 t=0,x=2,y=1 法线方程为y-1=2(x-2) 13,设/有在,y=nV则= dx Φ_∫' dy_f"(x)f(x)-[f"(x)P dx f(x) dr? f(x)
2 , 0 t t x e t y e − = = = 12.设 在 处法线方程 1 2 2 2 t t t dy e e dx e − − − = = − 2 2 ( ) ln[ ( )] d y f x y f x dx 13.设 存在, = = ,则 ( ) ( ) dy f x dx f x = 0 1 2 t dy dx = = − t x y = = = 0, 2, 1 法线方程为y x − = − 1 2( 2) 2 3 0 x y − − = 2 2 2 2 ( ) ( ) [ ( )] ( ) d y f x f x f x dx f x − =
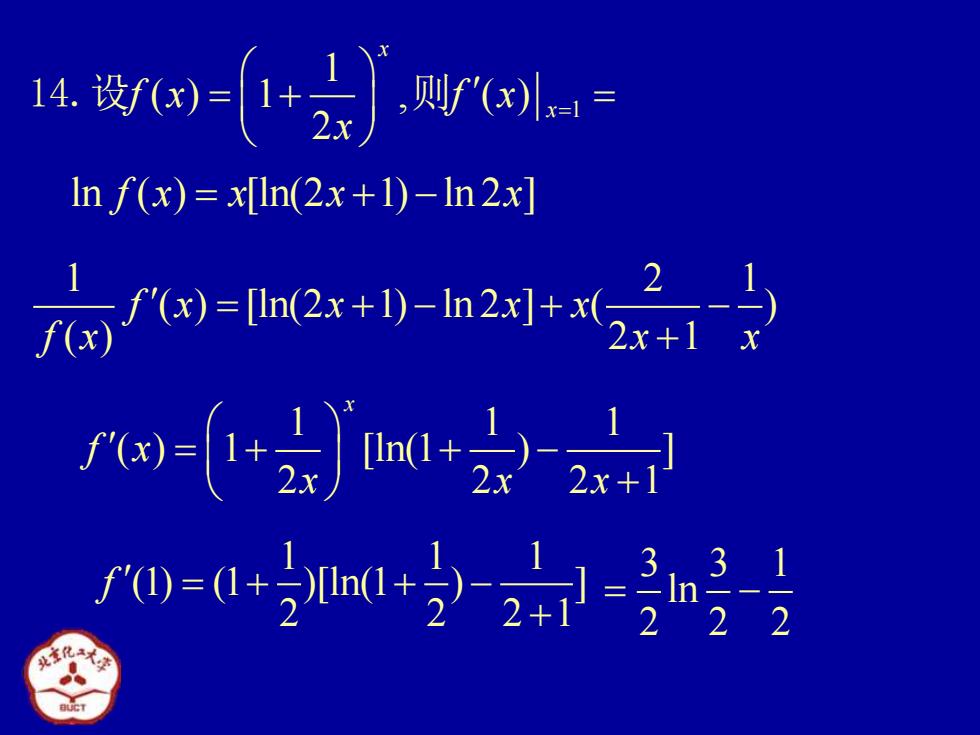
网=+】 则x In f(x)x[In(2x+1)-In 2x] 名网=m2x*)-h29t2名 w=2会m+22 w=0++宁-2-月
1 1 ( ) 1 , ( ) 2 x x f x f x x = = + = 14.设 则 ln ( ) [ln(2 1) ln 2 ] f x x x x = + − 1 2 1 ( ) [ln(2 1) ln 2 ] ( ) ( ) 2 1 f x x x x f x x x = + − + − + 1 1 1 ( ) 1 [ln(1 ) ] 2 2 2 1 x f x x x x = + + − + 1 1 1 (1) (1 )[ln(1 ) ] 2 2 2 1 f = + + − + 3 3 1 ln 2 2 2 = −

15.设y=tan2(1+2x2),则d= y=2tan(1+2x2)-sec2(1+2x2)4x dy 8xtan(1+2x2).sec2(1+2x2)dx 16.设函数)在x=处可导,1m)-/-力-1 h->0 2h 则f'(x)= 1m/)-f-2=1mf--/x】 h->0 2h h0 -2h 7f'(x)=-1 f'(x)=-2
2 2 15.设y x dy = + = tan (1 2 ),则 0 0 0 0 0 ( ) ( ) ( ) lim 1 2 ( ) h f x f x h f x x x h f x → − − = = − = 16.设函数 在 处可导, 则 2 2 2 y x x x = + + 2tan(1 2 ) sec (1 2 ) 4 2 2 2 dy x x x dx = + + 8 tan(1 2 ) sec (1 2 ) 0 f x ( ) 2 = − 0 0 0 0 0 0 ( ) ( ) ( ) ( ) lim lim h h 2 2 f x f x h f x h f x → → h h − − − − = − 0 1 ( ) 1 2 = = − f x

17.设点,3)是曲线y=ax+bx的拐点,则a=, b= y'3ax2 +2bx,y"6ax +2b 6a+2b=0,a+b=3 2 18.函数y=2x3-3x在区间[-1,4]上的最大值是80 y'=6x2-6x 令y=0,得x=0,x=1 -1)=-5,y(0)=0,y1)=-1,(4)=80
3 2 (1,3) y ax bx a b = + = = 17.设点 是曲线 的拐点,则 , 2 y ax bx y ax b = + = + 3 2 , 6 2 6 2 0, 3 a b a b + = + = 3 9 , 2 2 a b = − = 3 2 18.函数y x x = − 2 3 在区间[-1,4]上的最大值是 2 y x x = − 6 6 令y x x = = = 0, 0, 1 得 y y y y ( 1) 5, (0) 0, (1) 1, (4) 80 − = − = = − = 80