
《数值计算》课程教学大纲 一、课程基本信息 课程代码: 课程名称:数值计算 英文名称:Numerical Computation 课程类别:学科基础课 学 时: 48 学分: 3 适用对象: 考核方式:考试 先修课程 二、课程简介 数值分析是信息与计算科学专业学生选修的一门基础课程。课程通过对误差分析、插值方法、 数值积分与微分、方程求根等内容的讲授,使学生掌握数值分析的基本知识、基本原理和基本方 法,并具有设计简单算法解决实际问题的能力。课程主要内容包括误差分析、插值方法、数值积 分与微分、方程求根等。本课程将为后续课程的学习以及相关课程设计、毕业设计等奠定基础。 三、课程性质与教学目的 本课程主要介绍数值计算的基本方法以及数值计算研究中的一些较新的成果。以 数学分析、线性代数、高级语言程序设计为先行课,包含解线性方程组的直接法、解 线性方程组的迭代法、解非线性方程的迭代法、矩阵特征值与特征向量的计算、数据 拟合、多项式插值、数值积分与数值微分等基本内容,为微分方程数值解、最优化方 法、数学实验等后继课程作好准备。通过实验使学生掌握各种常用数值算法的构造原 理,提高算法设计和理论分析能力,为在计算机上解决科学计算问题打好基础。 四、教学内容及要求 第一章数值分析与科学计算引论 (一)目的与要求 深刻理解与熟练掌握有关误差的传播及误差分析:一般理解与掌握误差、 有效数字等相关概念 (二)教学内容 误差,误差的来源,绝对误差、相对误差,有效数字:简便的误差估计: 误差的传递与算法改变:计算过程中应注意的几个问题 重点:有关误差的传播及误差分析
1 《 数值计算 》课程教学大纲 一、课程基本信息 课程代码: 课程名称:数值计算 英文名称:Numerical Computation 课程类别: 学科基础课 学 时: 48 学 分: 3 适用对象: 考核方式:考试 先修课程: 二、课程简介 数值分析是信息与计算科学专业学生选修的一门基础课程。课程通过对误差分析、插值方法、 数值积分与微分、方程求根等内容的讲授,使学生掌握数值分析的基本知识、基本原理和基本方 法,并具有设计简单算法解决实际问题的能力。课程主要内容包括误差分析、插值方法、数值积 分与微分、方程求根等。本课程将为后续课程的学习以及相关课程设计、毕业设计等奠定基础。 三、课程性质与教学目的 本课程主要介绍数值计算的基本方法以及数值计算研究中的一些较新的成果。以 数学分析、线性代数、高级语言程序设计为先行课,包含解线性方程组的直接法、解 线性方程组的迭代法、解非线性方程的迭代法、矩阵特征值与特征向量的计算、数据 拟合、多项式插值、数值积分与数值微分等基本内容,为微分方程数值解、最优化方 法、数学实验等后继课程作好准备。通过实验使学生掌握各种常用数值算法的构造原 理,提高算法设计和理论分析能力,为在计算机上解决科学计算问题打好基础。 四、教学内容及要求 第一章 数值分析与科学计算引论 (一)目的与要求 深刻理解与熟练掌握有关误差的传播及误差分析;一般理解与掌握误差、 有效数字等相关概念。 (二)教学内容 误差,误差的来源,绝对误差、相对误差,有效数字;简便的误差估计; 误差的传递与算法改变;计算过程中应注意的几个问题 重点:有关误差的传播及误差分析

难点:有关误差的传播及误差分析 (三)数学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段使学生较好的 掌握本章的重点和难点。 第二章插值法 (一)目的与要求 深刻匣解与熟练堂握加何插值多顶式,分段插值函数,样条函数及混差估 般理解与掌握格朗日插值公式及其误差,均差与牛顿插值公式、误差, 分与牛 顿(向前、向后)插值公式、误差。 (二)教学内容 插值法与其必要性;格朗日插值公式及其误差:大区间样值处理:均差与 牛顿插值公式、误差:差分与牛顿(向前、向后)插值公式、误差:求导三 次插值公式:样条插值公式 点:如何插值多 分段插值函数,样条函数及误差估计 难点:插值多项式的求法。 (三)敦学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过插值法在现实生活中的例子,培养学生实 事求是,精益求精的工匠精神。 第三章函数逼近 (一)目的与要求 拉解与热练最小二法。了解线性拟合、低次多项式合及数 (二)教学内容 最小二乘法:线性拟合法:二、三次多项式拟合法:几类曲线拟合法:函 数类拟合法简介。 重点:最小二乘法,了解线性拟合、低次多项式拟合及函数拟合法 难点:最小二乘法求多项式 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过函数逼近在现实生活中的例子,培养学生 实事求是,精益求精的工匠精神。 第四章数值积分与数值微分 2
2 难点:有关误差的传播及误差分析 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段使学生较好的 掌握本章的重点和难点。 第二章 插值法 (一)目的与要求 深刻理解与熟练掌握如何插值多项式,分段插值函数,样条函数及误差估 计;一般理解与掌握格朗日插值公式及其误差,均差与牛顿插值公式、误差, 差分与牛顿(向前、向后)插值公式、误差。 (二)教学内容 插值法与其必要性;格朗日插值公式及其误差;大区间样值处理;均差与 牛顿插值公式、误差;差分与牛顿(向前、向后)插值公式、误差;求导三 次插值公式;样条插值公式。 重点:如何插值多项式,分段插值函数,样条函数及误差估计 难点:插值多项式的求法。 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过插值法在现实生活中的例子,培养学生实 事求是,精益求精的工匠精神。 第三章 函数逼近 (一)目的与要求 深刻理解与熟练掌握最小二乘法,了解线性拟合、低次多项式拟合及函数 拟合法。 (二)教学内容 最小二乘法;线性拟合法;二、三次多项式拟合法;几类曲线拟合法;函 数类拟合法简介。 重点:最小二乘法,了解线性拟合、低次多项式拟合及函数拟合法 难点:最小二乘法求多项式。 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过函数逼近在现实生活中的例子,培养学生 实事求是,精益求精的工匠精神。 第四章 数值积分与数值微分

(一)目的与要求 深刻理解与熟练掌握的内容有:了解龙贝格算法及高斯求积分 (二)教学内容 数值积分的必要性与粉值积分的特占,矩形法,梯形法,生师柯特斯公式 误差 复合 第形公式、复合抛物型公式及误差:步长半分的复合梯形,复合 抛物线型的简化算法:龙贝格算法:高斯求积公式:数值微分。 重点:数值积分和数值微分的三种基本方法,矩形法,梯形法,牛顿柯特斯公 式 难占:牛顿柯特斯公式 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过函数积分在现实生活中的例子,培养学生 实事求是,精益求精的工匠精神。 第五章解线性方程组的直接方法 (一)目的与要求 深刻了解与熟练掌握解线性方程的直接法。 (二)教学内容 解的存在性与唯一性:通消元法:列(行、大)主元素消去法;三角分解 与求解方法:追赶法:对称正定方程组的平方根法: 重点:解线性方程的直接法 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 第六章解线性方程组的迭代法 (一)目的与要求 了解方程求根的对分法和迭代法的求解过程。熟练掌握牛顿法。掌握弦截 (二)教学内容 二分法,解一元方程的迭代法,牛顿法,弦截法。 重点:迭代法,牛顷法。 难点:牛顿法。 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点 课程思政融 通过线性方程组在现实生活中的例子,培养 学生实事求是,精益求精的工匠精神
3 (一)目的与要求 深刻理解与熟练掌握的内容有:了解龙贝格算法及高斯求积分 (二)教学内容 数值积分的必要性与数值积分的特点;矩形法;梯形法;牛顿-柯特斯公式、 误差;复合梯形公式、复合抛物型公式及误差;步长半分的复合梯形,复合 抛物线型的简化算法;龙贝格算法;高斯求积公式;数值微分。 重点:数值积分和数值微分的三种基本方法,矩形法,梯形法,牛顿-柯特斯公 式 难点:牛顿-柯特斯公式。 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过函数积分在现实生活中的例子,培养学生 实事求是,精益求精的工匠精神。 第五章 解线性方程组的直接方法 (一)目的与要求 深刻了解与熟练掌握解线性方程的直接法。 (二)教学内容 解的存在性与唯一性;通消元法;列(行、大)主元素消去法;三角分解 与求解方法;追赶法;对称正定方程组的平方根法; 重点:解线性方程的直接法 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 第六章 解线性方程组的迭代法 (一)目的与要求 了解方程求根的对分法和迭代法的求解过程。熟练掌握牛顿法。掌握弦截 法。 (二)教学内容 二分法,解一元方程的迭代法,牛顿法,弦截法。 重点:迭代法,牛顿法。 难点:牛顿法。 (三)教学方法与手段 本章以课堂教学为主,并结合课堂练习与讨论,课后练习及答疑等手段 使学生较好的掌握本章的重点和难点。 课程思政融入主要体现:通过线性方程组在现实生活中的例子,培养 学生实事求是,精益求精的工匠精神
五、各教学环节学时分配 教学环节 习 讨 小 教学时数 论 实验 其他教 课 课 学环节 课程内容 第一章 3 3 第二章 第三章 12 第四章 4 9 第五章 6 6 第六章 9 合计 10 48 六、推荐教材和教学参考资源 选用教材: 李庆扬,王能超,易大义,数值分析(第5版),清华大学出版社2008/12/1。 教学参考资源: 1.Curtis F.Gerald,.PatrickO.Wheatley,应用数值分析,机械工业出版社,20o6 2.李林、金先级,数值计算方法,中山大学出版社2006年2月版. 七、其他说明 1,修订大纲的指导思想:根据专业特点,使学生掌握必备的数值计算基本理论和 基本方法,为学习后继专业课程、从事科学研究或工程技术打下一定的基础。 果程 课程和后续课程的联系 :先修课程解决该课程所必须的数 学基寄,不疾橙署量酬死装系续实程者生处理因给构图 大纲中打星号的部分,教师可根据实际情况选择是否讲解。 大纲修订人: 吕律 修订日期:2017,9-10 大纲审定人: 刘国刚 审定日期:2017,9-10
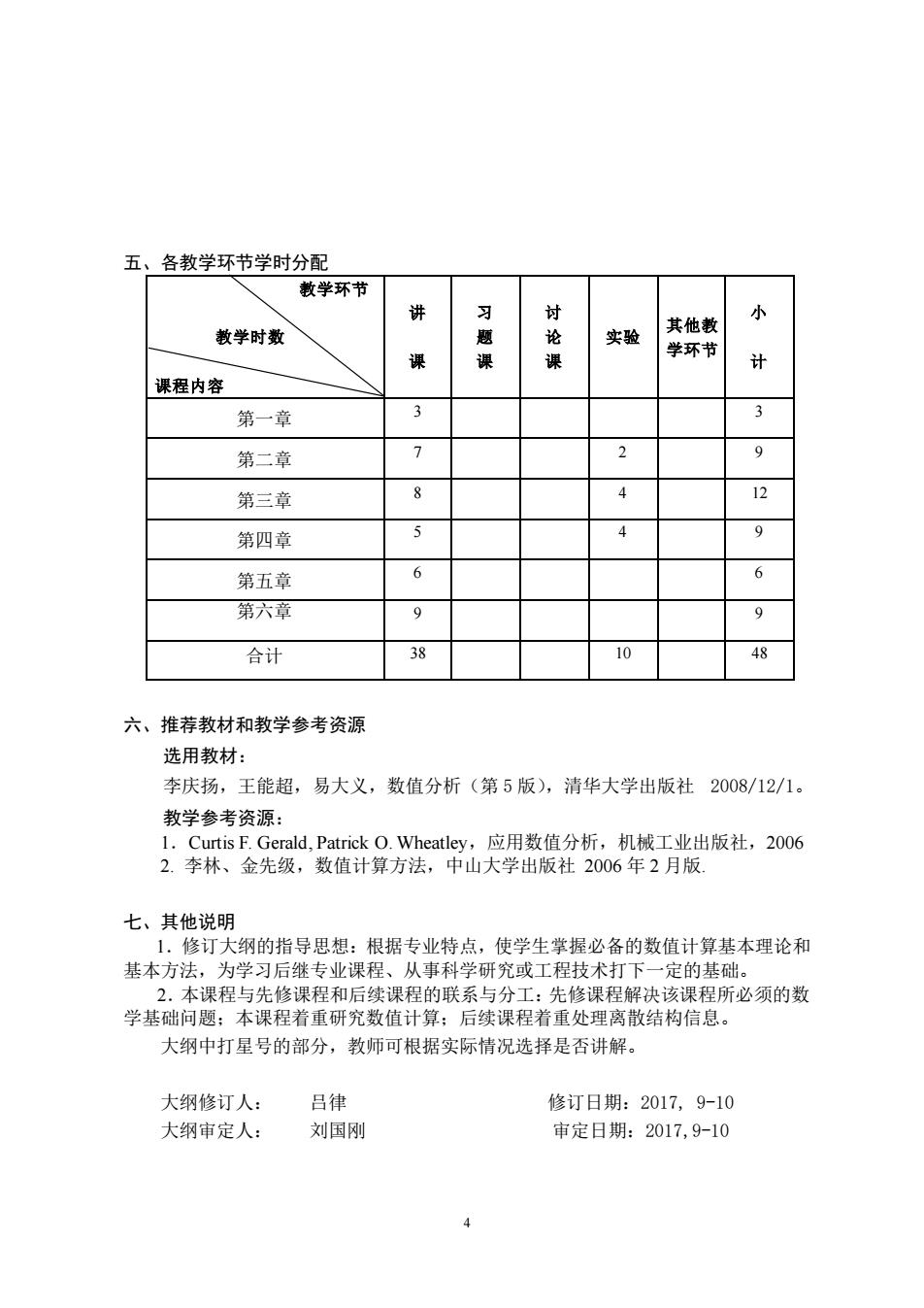
4 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 3 3 第二章 7 2 9 第三章 8 4 12 第四章 5 4 9 第五章 6 6 第六章 9 9 合计 38 10 48 六、推荐教材和教学参考资源 选用教材: 李庆扬,王能超,易大义,数值分析(第 5 版),清华大学出版社 2008/12/1。 教学参考资源: 1.Curtis F. Gerald, Patrick O. Wheatley,应用数值分析,机械工业出版社,2006 2. 李林、金先级,数值计算方法,中山大学出版社 2006 年 2 月版. 七、其他说明 1.修订大纲的指导思想:根据专业特点,使学生掌握必备的数值计算基本理论和 基本方法,为学习后继专业课程、从事科学研究或工程技术打下一定的基础。 2.本课程与先修课程和后续课程的联系与分工:先修课程解决该课程所必须的数 学基础问题;本课程着重研究数值计算;后续课程着重处理离散结构信息。 大纲中打星号的部分,教师可根据实际情况选择是否讲解。 大纲修订人: 吕律 修订日期:2017, 9-10 大纲审定人: 刘国刚 审定日期:2017,9-10

5
5