
“Probabi lity”Course Syl labus 1、Course Information Course Code:20100043 Course Name:Probability Course Type:Basic Major Course Credit Hour:48 Credit:3 Objective Students:Grade2020,Statistics Evaluation Mode:Examination Prerequisite Course:Mathematical analysis,Advanced Algebra 2.Course Introduction Probability is a subject with wide application in finance,insurance,stocks,security, and many other fields in engineering technology and natural science.It brings a lot of fundamental tools for analysis and solving problems in many subjects.The combinations of probability and other areas form a variety of branch of disciplines. Through the study of this course.the students should systematically master the basic knowledge of probability,as well as the fundamental ideas and methods to handle random phenomena,and thus lays a solid foundation for the following courses 3、课程性质与教学目的 Probability is a mathematical discipline that study the objective laws of random phenomena.It is an important basic theoretical and major compulsory course for undergraduates majoring in statistics,applied statistics,and applied mathematics Through the study of this course,students should master the basic concepts of probability theory,understand its basic theories and methods,so that gain a primary To 1
1 “Probability” Course Syllabus 1、Course Information Course Code: 20100043 Course Name: Probability Course Type: Basic Major Course Credit Hour: 48 Credit: 3 Objective Students: Grade2020, Statistics Evaluation Mode: Examination Prerequisite Course: Mathematical analysis, Advanced Algebra 2、Course Introduction Probability is a subject with wide application in finance, insurance, stocks, security, and many other fields in engineering technology and natural science. It brings a lot of fundamental tools for analysis and solving problems in many subjects. The combinations of probability and other areas form a variety of branch of disciplines. Through the study of this course, the students should systematically master the basic knowledge of probability, as well as the fundamental ideas and methods to handle random phenomena, and thus lays a solid foundation for the following courses. 3、课程性质与教学目的 Probability is a mathematical discipline that study the objective laws of random phenomena. It is an important basic theoretical and major compulsory course for undergraduates majoring in statistics, applied statistics, and applied mathematics. Through the study of this course, students should master the basic concepts of probability theory, understand its basic theories and methods, so that gain a primary To

comprehend of the basic ideas and methods to handle random events,and develop the ability to use probability theory to analyze and solve practical problems This course is mainly taught in class,with an emphasis on the basic ideas of probability, and a target to master the basic probability methods and to develop basic computational ability,analytical ability and problem-solving ability as well.Meanwhile,the students should gain some knowledge on the history of combinatorial analysis and probability. particularly on the contribution of Chinese mathematicians on these fields.And they should leam some philosophy of living that reflected in the laws and theorems of probability theory. 4.Content and Requirements Module 1 Combinatorial Analysis (1)Purpose and Requirements 1.To comprehend the basic concepts of permutation and combination 2.To master the basic principle of counting 3.To comprehend the idea and theorem of multinomial coefficients (2) Contents 1.Main Content:Basic principle of counting,permutations,combinations, multinomial coefficients 2.Basic Concepts and Knowledge Points:The basic principle of counting the concept of permutation and combination.the multinomial theorem 3.Problems and Application (Ability Requirements):Application of techniques to solve counting problems on permutation and combination (3)Thinking and Practice Use the basic idea of permutation and combination counting to solve some real-world counting problems.Ideological and political education:introduction of great Chinese in combinatorial analysis:Hui Yang.Shanlan Li
2 comprehend of the basic ideas and methods to handle random events, and develop the ability to use probability theory to analyze and solve practical problems. This course is mainly taught in class, with an emphasis on the basic ideas of probability, and a target to master the basic probability methods, and to develop basic computational ability, analytical ability and problem-solving ability as well. Meanwhile, the students should gain some knowledge on the history of combinatorial analysis and probability, particularly on the contribution of Chinese mathematicians on these fields. And they should learn some philosophy of living that reflected in the laws and theorems of probability theory. 4、Content and Requirements Module 1 Combinatorial Analysis (1) Purpose and Requirements 1.To comprehend the basic concepts of permutation and combination 2.To master the basic principle of counting 3.To comprehend the idea and theorem of multinomial coefficients (2) Contents Section 1 1.Main Content: Basic principle of counting, permutations, combinations, multinomial coefficients 2.Basic Concepts and Knowledge Points: The basic principle of counting, the concept of permutation and combination, the multinomial theorem 3.Problems and Application (Ability Requirements): Application of techniques to solve counting problems on permutation and combination (3) Thinking and Practice Use the basic idea of permutation and combination counting to solve some real-world counting problems. Ideological and political education: introduction of great Chinese in combinatorial analysis: Hui Yang, Shanlan Li

(4)Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching. multimedia teaching,network-assisted teaching,and class discussion. Module 2 Axioms of Probability (1)Purpose and Requirements 1.To comprehend the concepts of sample space and events 2.To comprehend the axioms of probability 3.Master some properties of probability in the form of propositions 4.Master some techniques in probability analysis (2) Contents Section 1 1.Main Content:Sample space,events,axioms of probability,propositions on probabilities,probability as a measure of belief 2.Basic Concepts and Knowledge Points:The concept of sample space and events,the axioms of probability,some basic propositions on probabilities 3.Problems and Application(Ability Requirements):Identifying the sample space and events in given problems.using some propositions to analyze some application problems (3)Thinking and Practice: To have a deeper comprehension of why we need to formulate the axioms of probability.Ideological and political education:introduction of great Chinese in probability:Kai Lai Chung,Baolu Xu (4)Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching. multimedia teaching.network-assisted teaching.and class d iscussion Module 3 Conditional Probability and Independence (1) Purpose and Requirements 1.To comprehend the concept of conditional probability 2.To comprehend the Bayes'formula 3.To comprehend the concept of independence 4.To master the application of conditional probability and Bayes'formula (2) Contents Section I 3
3 (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 2 Axioms of Probability (1) Purpose and Requirements 1.To comprehend the concepts of sample space and events 2.To comprehend the axioms of probability 3.Master some properties of probability in the form of propositions 4.Master some techniques in probability analysis (2) Contents Section 1 1.Main Content: Sample space, events, axioms of probability, propositions on probabilities, probability as a measure of belief 2.Basic Concepts and Knowledge Points: The concept of sample space and events, the axioms of probability, some basic propositions on probabilities 3.Problems and Application (Ability Requirements): Identifying the sample space and events in given problems, using some propositions to analyze some application problems (3) Thinking and Practice: To have a deeper comprehension of why we need to formulate the axioms of probability. Ideological and political education: introduction of great Chinese in probability: Kai Lai Chung, Baolu Xu. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 3 Conditional Probability and Independence (1) Purpose and Requirements 1.To comprehend the concept of conditional probability 2.To comprehend the Bayes’ formula 3.To comprehend the concept of independence 4.To master the application of conditional probability and Bayes’ formula (2) Contents Section 1

1.Main Content:Conditional probabilities,Bayes'formula.Independent events 2.Basic Concepts and Knowledge Points:The concept of conditional probabilities,the ideas and applications of the Bayes'formula,the concept of independence and the analysis of independent events 3.Problems and Application (Ability Requirements):Using the conditional probability formula and Bayes'formula to analyze some probability problems (3)Thinking and Practice Some further reading and studying on the Bayes networks.A discussion on the Monty Hall problem(three gate problem).Ideological and political education:why telling lies repeatedly lower one's credibility? (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching. multimedia teaching.network-assisted teaching.and class discussion Module 4 Random variables (1)Purpose and Requirements 1.To comprehend the concept of random variables and discrete random variables 2. To comprehend the concept of expectation and variance 3.To master Bemnoulli and binomial probability distributions 4.To master Poisson probability distribution 5.To master several other important probability distributions 6.To comprehend the concept of and to master the computation of cumulative distribution (2) Contents Section 1 1.Main Content:Random variables,Discrete Random variables,expectation value,expectation value of a function,variance,Bemoulli and binomial random variables.Poisson random variable.some other discrete probability distribution,expected value of sums of random variables cumulative distribution function 2.Basic Concepts and Knowledge Points:Random variable,discrete random variable,expectation value,variance,Bernoulli random variable,binomial 4
4 1.Main Content: Conditional probabilities, Bayes’ formula, Independent events 2.Basic Concepts and Knowledge Points: The concept of conditional probabilities, the ideas and applications of the Bayes’ formula, the concept of independence and the analysis of independent events 3.Problems and Application (Ability Requirements): Using the conditional probability formula and Bayes’ formula to analyze some probability problems (3) Thinking and Practice Some further reading and studying on the Bayes networks. A discussion on the Monty Hall problem (three gate problem). Ideological and political education: why telling lies repeatedly lower one’s credibility? (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 4 Random variables (1) Purpose and Requirements 1.To comprehend the concept of random variables and discrete random variables 2.To comprehend the concept of expectation and variance 3.To master Bernoulli and binomial probability distributions 4.To master Poisson probability distribution 5.To master several other important probability distributions 6.To comprehend the concept of and to master the computation of cumulative distribution (2) Contents Section 1 1.Main Content: Random variables, Discrete Random variables, expectation value, expectation value of a function, variance, Bernoulli and binomial random variables, Poisson random variable, some other discrete probability distribution, expected value of sums of random variables, cumulative distribution function 2.Basic Concepts and Knowledge Points: Random variable, discrete random variable, expectation value, variance, Bernoulli random variable, binomial

random variable,Poisson random variable,cumulative distribution 3.Problems and Application(Ability Requirements):Use the concept of random variable,expectation value and variance to model some real-world problems (3)Thinking and Practice Using Bemoulli,binomial,Poisson and other probability distribution to model and analyze the problems appear in applications. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching. multimed ia teaching,network-assisted teaching,and class discussion. Module 5 Continuous Random variables (1)Purpose and Requirements 1.To comprehend the concept of continuous probability distribution and continuous random variables 2.To comprehend uniform probability distribution 3.To comprehend normal probability distribution 4.To comprehend exponential probability distribution 5.To master the computation of functions of random variables (2)Contents 1.Main Content:Expectation of continuous random variables,variance of continuous random variables,uniform random variable,normal random variable.exponential random variable.the distribution of a function of a random variable 2.Basic Concepts and Knowledge Points:continuous random variable, uniform probability distribution,normal probability distribution, exponential probability distribution,the probability distribution of a function 3.Problems and Application(Ability Requirements):Use continuous random variable and the concept of the probability distribution of a function to model and solve some problems. (3)Thinking and Practice Using uniform,normal,exponential and other probability distribution to model and analyze the problems appear in applications. 5
5 random variable, Poisson random variable, cumulative distribution 3.Problems and Application (Ability Requirements): Use the concept of random variable, expectation value and variance to model some real-world problems. (3) Thinking and Practice Using Bernoulli, binomial, Poisson and other probability distribution to model and analyze the problems appear in applications. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 5 Continuous Random variables (1) Purpose and Requirements 1.To comprehend the concept of continuous probability distribution and continuous random variables 2.To comprehend uniform probability distribution 3.To comprehend normal probability distribution 4.To comprehend exponential probability distribution 5.To master the computation of functions of random variables (2) Contents Section 1 1.Main Content: Expectation of continuous random variables, variance of continuous random variables, uniform random variable, normal random variable, exponential random variable, the distribution of a function of a random variable 2.Basic Concepts and Knowledge Points: continuous random variable, uniform probability distribution, normal probability distribution, exponential probability distribution, the probability distribution of a function 3.Problems and Application (Ability Requirements): Use continuous random variable and the concept of the probability distribution of a function to model and solve some problems. (3) Thinking and Practice Using uniform, normal, exponential and other probability distribution to model and analyze the problems appear in applications

(4)Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching,network-assisted teaching,and class discussion. Module 6 Joint distributed random variables (1) Purpose and Requirements 1.To comprehend the idea and concept of joint distribution 2.To comprehend the concept of independence and independent random variable 3.To comprehend the concept of discrete conditional distributions 4.To comprehend the concept of continuous conditional distribution 5.Master the methods to compute joint distribution of random variables (2) Contents Section 1 1.Main Content:Joint distribution function,independent random variables and their sum,discrete conditional distributions,continuous conditional distributions,joint distribution of functions of random variables 2.Basic Concepts and Knowledge Points:Joint distribution,independence, discrete conditional distribution,continuous conditional distribution,joint distribution of functions 3.Problems and Application(Ability Requirements):The application of joint distribution.independence and conditional distribution. (3)Thinking and Practice Identify the situations in applications that we need to use joint distribution as models and use joint distribution function to solve some problems.Ideological and political education:How to quantitatively describe real-world phenomena. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching multimedia teaching,network-assisted teaching,and class discussion. Module 7 Properties of Expectation (1)Purpose and Requirements 1.To master the computation ofexpectation of sums 2.To comprehend the concept of moment 3.To master the computation of covariance of sums 6
6 (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 6 Joint distributed random variables (1) Purpose and Requirements 1.To comprehend the idea and concept of joint distribution 2.To comprehend the concept of independence and independent random variable 3.To comprehend the concept of discrete conditional distributions 4.To comprehend the concept of continuous conditional distributions 5.Master the methods to compute joint distribution of random variables (2) Contents Section 1 1.Main Content: Joint distribution function, independent random variables and their sum, discrete conditional distributions, continuous conditional distributions, joint distribution of functions of random variables 2.Basic Concepts and Knowledge Points: Joint distribution, independence, discrete conditional distribution, continuous conditional distribution, joint distribution of functions 3.Problems and Application (Ability Requirements): The application of joint distribution, independence and conditional distribution. (3) Thinking and Practice Identify the situations in applications that we need to use joint distribution as models and use joint distribution function to solve some problems. Ideological and political education: How to quantitatively describe real-world phenomena. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 7 Properties of Expectation (1) Purpose and Requirements 1.To master the computation of expectation of sums 2.To comprehend the concept of moment 3.To master the computation of covariance of sums

4.To master the computation of variance of sums 5.To comprehend the concept of correlation 6.To comprehend the concept of moment generating function (2) Contents Section 1 1.Main Content:Expectation of sums of random variables,moments, covariance of sums,variance of sums,correlation,conditional expectation. moment generating function 2.Basic Concepts and Knowledge Points:Expectation of sums,moment, covariance and variance of sums,correlation,generating function 3.Problems and Application(Ability Requirements):Application of the ideas of expectation,moment,covariance,variance in modeling and analysis of problems. (3)Thinking and Practice Identify the situations in applications that we need to use joint distribution as models and use joint distribution function to solve some problems. (4)Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching. multimedia teaching,network-assisted teaching.and class discussion Module 8 Limit Theorem (1)Purpose and Requirements 1.To comprehend the weak law of large number 2.To comprehend the strong law of large number 3.To comprehend the central limit theorem 4.To comprehend Chebyshev's inequality and some other inequalities 5.To master the application of Chebyshev's and other inequality (2)Contents Section1 1.Main Content:Chebyshey's inequality.weak law of large number.central limit theorem,strong law of large numbers,some other inequalities, bounding the error probability 2.Basic Concepts and Knowledge Points:Weak law of large number,strong law of large number,Chebyshev's inequalities and other inequalities. central limit theorem
7 4.To master the computation of variance of sums 5.To comprehend the concept of correlation 6.To comprehend the concept of moment generating function (2) Contents Section 1 1.Main Content: Expectation of sums of random variables, moments, covariance of sums, variance of sums, correlation, conditional expectation, moment generating function 2.Basic Concepts and Knowledge Points: Expectation of sums, moment, covariance and variance of sums, correlation, generating function 3.Problems and Application (Ability Requirements): Application of the ideas of expectation, moment, covariance, variance in modeling and analysis of problems. (3) Thinking and Practice Identify the situations in applications that we need to use joint distribution as models and use joint distribution function to solve some problems. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. Module 8 Limit Theorem (1) Purpose and Requirements 1.To comprehend the weak law of large number 2.To comprehend the strong law of large number 3.To comprehend the central limit theorem 4.To comprehend Chebyshev’s inequality and some other inequalities 5.To master the application of Chebyshev’s and other inequality (2) Contents Section 1 1.Main Content: Chebyshev’s inequality, weak law of large number, central limit theorem, strong law of large numbers, some other inequalities, bounding the error probability 2.Basic Concepts and Knowledge Points: Weak law of large number, strong law of large number, Chebyshev’s inequalities and other inequalities, central limit theorem
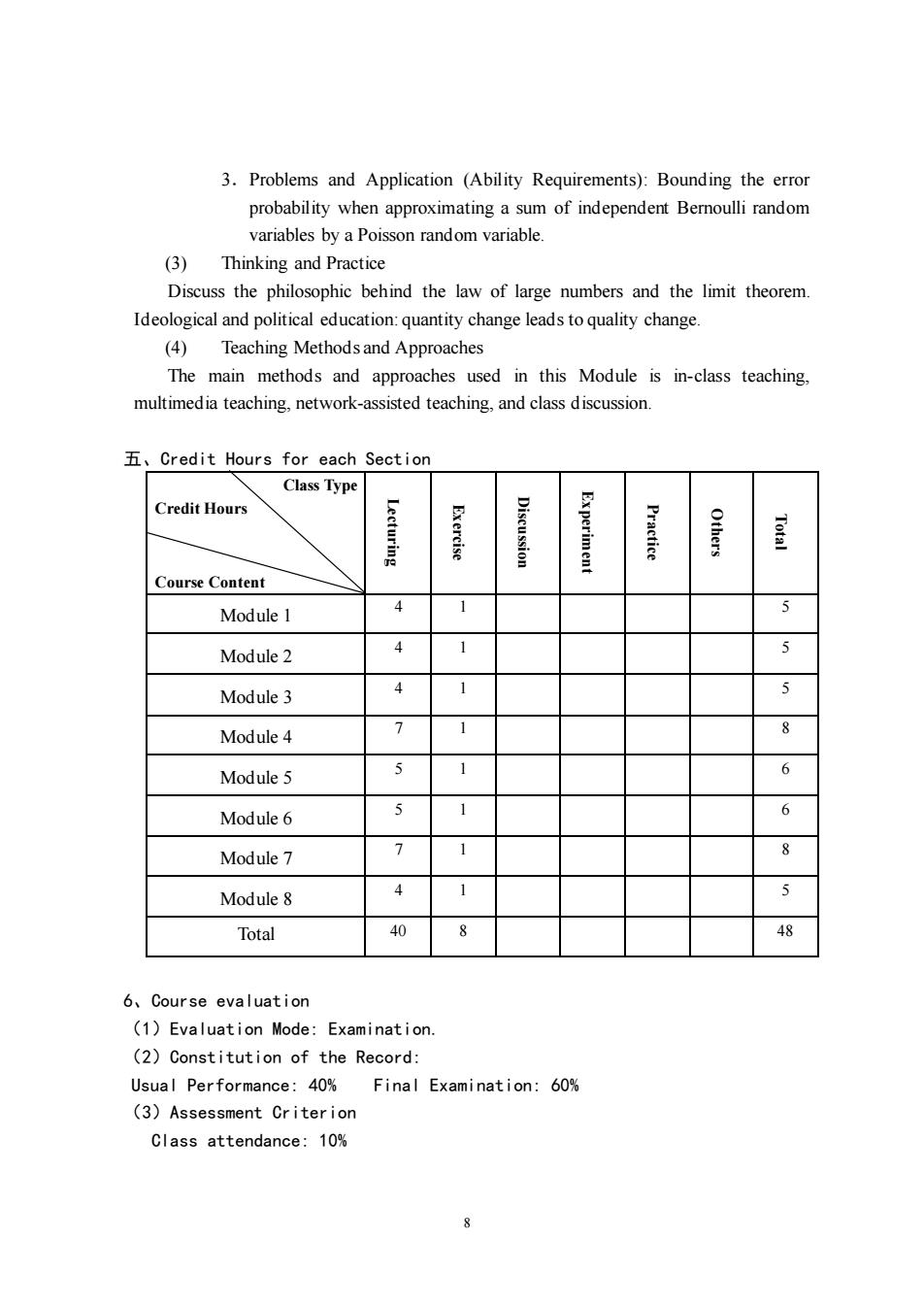
3.Problems and Application (Ability Requirements):Bounding the error probability when approximating a sum of independent Bemoulli random variables by a Poisson random variable. (3)Thinking and Practice Discuss the philosophic behind the law of large numbers and the limit theorem. Ideological and political education:quantity change leads to quality change. (4)Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching,network-assisted teaching,and class discussion. 五、Credit Hours for each Section Class Type Credit Hours men Course Content Module1 Module 2 Module3 Module4 Module 5 6 Module 6 6 Module7 Module 8 Total 8 6、Course evaluation (1)Evaluation Mode:Examination. (2)Constitution of the Record: Usual Performance:40% Final Examination:60% (3)Assessment Criterion Class attendance:10%
8 3.Problems and Application (Ability Requirements): Bounding the error probability when approximating a sum of independent Bernoulli random variables by a Poisson random variable. (3) Thinking and Practice Discuss the philosophic behind the law of large numbers and the limit theorem. Ideological and political education: quantity change leads to quality change. (4) Teaching Methods and Approaches The main methods and approaches used in this Module is in-class teaching, multimedia teaching, network-assisted teaching, and class discussion. 五、Credit Hours for each Section Class Type Credit Hours Course Content Lecturing Exercise Discussion Experiment Practice Others Total Module 1 4 1 5 Module 2 4 1 5 Module 3 4 1 5 Module 4 7 1 8 Module 5 5 1 6 Module 6 5 1 6 Module 7 7 1 8 Module 8 4 1 5 Total 40 8 48 6、Course evaluation (1)Evaluation Mode: Examination. (2)Constitution of the Record: Usual Performance: 40% Final Examination: 60% (3)Assessment Criterion Class attendance: 10%

In-class performance:10% Usual homework:20% Final Examination:60% Recommended textbooks and teaching resources [1]S.M.Ross.Afirst course in probability (Ed9).Beijing:China Machine Press,2017. [2]K.LChung.Acourse in probability theory (Ed3).Beijing:China Machine Press,2010 [3]K.L Chung.Elementary probability theory (Ed4).Beijing:World Publishing Corporation,2010. [4]Feiler An introduction to probability theory and its application Beijing:People's Posts and Telecommunication Press,2005. [5]Shuyuan He.Probability.Beijing:Peking University Press,006. 八、Remarks The prerequisite course of this course is mathematical analysis and advanced algebra.and the subsequent courses include mathematical statistics and data analysis. Revised by(大纲修订人):Zanbo Zhang张赞波Date(修订日期):2020.12 Reviewed by(大纲审定人): Date(审定日期):
9 In-class performance: 10% Usual homework: 20% Final Examination: 60% 七、Recommended textbooks and teaching resources [1] S.M. Ross. A first course in probability (Ed9). Beijing: China Machine Press, 2017. [2] K.L. Chung. A course in probability theory (Ed3). Beijing: China Machine Press, 2010. [3] K.L. Chung. Elementary probability theory (Ed4). Beijing: World Publishing Corporation, 2010. [4] Feiler. An introduction to probability theory and its application. Beijing: People’s Posts and Telecommunication Press, 2005. [5] Shuyuan He. Probability. Beijing: Peking University Press, 2006. 八、Remarks The prerequisite course of this course is mathematical analysis and advanced algebra, and the subsequent courses include mathematical statistics and data analysis. Revised by (大纲修订人):Zanbo Zhang 张赞波 Date (修订日期):2020.12 Reviewed by (大纲审定人): Date (审定日期):