
《现代多元统计分析(双语)》课程教学大纲 一、课程基本信息 课程代码:20100053 课程名称:现代多元统计分析(双语) 英文名称:Multivariate Statistical Analysis 课程类别:专业基础课 时:48 学 分:3 适用对象:中外联合培养项目 考核方式:考试 先修课程:高等代数、概率论、数理统计 二、课程简介 中文简介 多元统计分析是高等学校统计学专业的一门必修的专业基础课程。本课程以统计 思想为主线,介绍各种多元统计方法的应用。课程主要内容包括多元正态总体的假设 检验、判别分析、聚类分析、主成分分析、因子分析等常用的多元统计方法。通过本 课程的学习,使学生掌握多元统计方法的基本原理,提高学生分析并解决问题的能力。 英文简介 Multivariate statistical analysis is a basic course of statistics in university.This course introduces the application of various multivariate statistical methods by taking the statistical thought as principal line.This course covers various commonly used multivariate statistical methods,such as hypothesis test of multivariate normal population,discriminant analysis, cluster analysis,principal com analysis,factor analysis and so on Through studying this course,students will master the basic principles of multivariate statistical methods,and improve the ability to analyze and solve problems. 三、课程性质与教学目的 《现代多元统计分析》研究的是多个变量的统计总体,这使它能够一次性处理多 个变量的庞杂数据,而不需要考虑异度量的问题,即它是处理多个变量的综合分析方 法。它可以把多个变量对一个或多个变量的作用程度大小线性地表示出来,反映事物 多变量间的相互关系:可以消除多个变量的共线性,将高维空间的问题降至低维空间
1 《现代多元统计分析(双语)》课程教学大纲 一、课程基本信息 课程代码:20100053 课程名称:现代多元统计分析(双语) 英文名称:Multivariate Statistical Analysis 课程类别:专业基础课 学 时:48 学 分:3 适用对象: 中外联合培养项目 考核方式:考试 先修课程:高等代数、概率论、数理统计 二、课程简介 中文简介 多元统计分析是高等学校统计学专业的一门必修的专业基础课程。本课程以统计 思想为主线,介绍各种多元统计方法的应用。课程主要内容包括多元正态总体的假设 检验、判别分析、聚类分析、主成分分析、因子分析等常用的多元统计方法。通过本 课程的学习,使学生掌握多元统计方法的基本原理,提高学生分析并解决问题的能力。 英文简介 Multivariate statistical analysis is a basic course of statistics in university. This course introduces the application of various multivariate statistical methods by taking the statistical thought as principal line. This course covers various commonly used multivariate statistical methods, such as hypothesis test of multivariate normal population, discriminant analysis, cluster analysis, principal component analysis, factor analysis and so on. Through studying this course, students will master the basic principles of multivariate statistical methods, and improve the ability to analyze and solve problems. 三、课程性质与教学目的 《现代多元统计分析》研究的是多个变量的统计总体,这使它能够一次性处理多 个变量的庞杂数据,而不需要考虑异度量的问题,即它是处理多个变量的综合分析方 法。它可以把多个变量对一个或多个变量的作用程度大小线性地表示出来,反映事物 多变量间的相互关系;可以消除多个变量的共线性,将高维空间的问题降至低维空间

中,在尽量保存原始信息的前提下,消除重叠信息,简化变量间的关系:可以通过事 物的表象,挖据事物深层次的、不可直接观测到的属性即引起事物变化的本质:也可 以透过繁杂事物的某些性质,将事物进行识别、归类。 本课程的教学目的在于让学生熟练掌握多种多元统计方法的基本思想,数学原理 的基础上,能够把大量的数据简化到人们能够处理的范围之内,能够构造一个综合指 标代替原来的变量,能够进行判别和分类,能够对数学计算结果进行科学合理的解释, 并从专业背景上给予分析:能将统计分析方法应用至实际中去,为避免繁冗的数学计 算,本课程要求学生学会使用R语言或SAS软件的相关功能。 四、教学内容及要求 第一章随机向量 (一)目的与要求 1.了解多元分布、数字特征、欧氏距离和马氏距离的概念 2.领会随机向量的变换、特征函数的概念。 3.掌握多元分布的定义、欧氏距离的定义和计算 (二)教学内容 第一节多元分布 1.主要内容 由随机变量的分布推出随机向量的分布 2.基本概念和知识点 随机向量、多元概率分布函数、多元概率密度函数、边缘分布、条件 分布、独立性 第二节数字特征 1.主要内容 随机向量与随机矩阵的数字特征 2,基本概念和知识点 数学期望、协方差矩阵、不相关、相关矩阵、广义方差 第三节欧氏距离和马氏距离 1.主要内容 两种常见距离的性质与计算 2.基本概念和知识点 欧氏距离的性质与计算、马氏距离的性质与计算 3.问题与应用(能力要求)
2 中,在尽量保存原始信息的前提下,消除重叠信息,简化变量间的关系;可以通过事 物的表象,挖掘事物深层次的、不可直接观测到的属性即引起事物变化的本质;也可 以透过繁杂事物的某些性质,将事物进行识别、归类。 本课程的教学目的在于让学生熟练掌握多种多元统计方法的基本思想,数学原理 的基础上,能够把大量的数据简化到人们能够处理的范围之内,能够构造一个综合指 标代替原来的变量,能够进行判别和分类,能够对数学计算结果进行科学合理的解释, 并从专业背景上给予分析;能将统计分析方法应用至实际中去,为避免繁冗的数学计 算,本课程要求学生学会使用 R 语言或 SAS 软件的相关功能。 四、教学内容及要求 第一章 随机向量 (一)目的与要求 1.了解多元分布、数字特征、欧氏距离和马氏距离的概念。 2.领会随机向量的变换、特征函数的概念。 3.掌握多元分布的定义、欧氏距离的定义和计算 (二)教学内容 第一节 多元分布 1.主要内容 由随机变量的分布推出随机向量的分布 2.基本概念和知识点 随机向量、多元概率分布函数、多元概率密度函数、边缘分布、条件 分布、独立性 第二节 数字特征 1.主要内容 随机向量与随机矩阵的数字特征 2.基本概念和知识点 数学期望、协方差矩阵、不相关、相关矩阵、广义方差 第三节 欧氏距离和马氏距离 1.主要内容 两种常见距离的性质与计算 2.基本概念和知识点 欧氏距离的性质与计算、马氏距离的性质与计算 3. 问题与应用(能力要求)

理解马氏距离的编制思想 (三)思考与实践 引入国家对于企业数据收集方式的改进措施,使学生了解我国对于数据真 实性的重视,树立数据必须真实可靠的观念。 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第二章多元正态分布 (一)目的与要求 1.了解多元正态分布基本概念和定义 2.领会名元正态分布的重要性质 3.掌握多元正态分布密度函数及其数字特征的解析表达式、数字特征的 其木性质 (二)教学内容 第一节多元正态分布的定义 1.主要内容 了解多元正态分布的定义 2.基本概念和知识点 p元正态分布的概率密度、非退化多元正态分布、概率密度等高线 第二节多元正态分布的性质 1.主要内容 多元正态分布的重要性质 2.基本概念和知识点 多元正态分布的11条重要性质 第三节极大似然估计及估计量的性质 1.主要内容 多元正态分布的极大似然估计及其性质 2.基本概念和知识点 极大似然估计、无偏性、有效性、一致最小方差无偏估计、一致性、 充分估计量 第四节复相关系数和偏相关系数 1.主要内容 复相关系数和偏相关系数的性质与计算 2.基本概念和知识点 复相关系数、样本复相关系数、偏相关系数、样本偏相关系数 3
3 理解马氏距离的编制思想 (三)思考与实践 引入国家对于企业数据收集方式的改进措施,使学生了解我国对于数据真 实性的重视,树立数据必须真实可靠的观念。 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第二章 多元正态分布 (一)目的与要求 1.了解多元正态分布基本概念和定义 2.领会多元正态分布的重要性质 3.掌握多元正态分布密度函数及其数字特征的解析表达式、数字特征的 基本性质 (二)教学内容 第一节 多元正态分布的定义 1.主要内容 了解多元正态分布的定义 2.基本概念和知识点 p 元正态分布的概率密度、非退化多元正态分布、概率密度等高线 第二节 多元正态分布的性质 1.主要内容 多元正态分布的重要性质 2.基本概念和知识点 多元正态分布的 11 条重要性质 第三节 极大似然估计及估计量的性质 1.主要内容 多元正态分布的极大似然估计及其性质 2.基本概念和知识点 极大似然估计、无偏性、有效性、一致最小方差无偏估计、一致性、 充分估计量 第四节 复相关系数和偏相关系数 1.主要内容 复相关系数和偏相关系数的性质与计算 2.基本概念和知识点 复相关系数、样本复相关系数、偏相关系数、样本偏相关系数

第五节不和(n-1)S的抽样分布 1.主要内容 样本均值向量和样本标准差的抽样分布 2.基本概念和知识点 样本均值的抽样分布、多元中心极限定理、威沙特分布 (三)思考与实践 通过介绍t分布的发现,说明在统计工作中要重视细徽差别,要做细心谨慎 的统计人 (四)教学方法与毛段 课堂讲授、多媒体教学,上机实操 第三章多元正态总体的统计推断 (一)目的与要求 1.了解几个常见的统计检验量服从的概率分布 2.理解样本统计量和根据显著性水平查表所得值之间的比较与最终接受 或拒绝原假设之间的关系。 3.掌握均值向量检验在实际经济研究中的应用,以及两总体及多总体均 值向量检验的应用意义。 4.理解协方差阵检验的应用意义,特别要学会两个检验结合运用 (二)教学内容 第二节单个总体均值的推断 1.主要内容 均值向量的检验,HotellingT分布及其性质,置信区域,联合置信区 间,均值向量的大样本推断 2.基本概念和知识点 HotellingT2分布,置信区域,联合置信区间,均值向量的大样本推 断 3.问题与应用(能力要求) 理解交并原则,能推导总体协方差阵未知时的检验统计量:理解置信 区域与联合置信区间的关系:理解拉奥悖论 第三节两个总体均值的比较推断 1.主要内容 两个独立样本情形及成对试验情形下的两个总体均值的比较推断 2.基本概念和知识点 总体协方差阵的联合无偏估计,成对试验
4 第五节 x 和 ( 1) n S − 的抽样分布 1.主要内容 样本均值向量和样本标准差的抽样分布 2.基本概念和知识点 样本均值的抽样分布、多元中心极限定理、威沙特分布 (三)思考与实践 通过介绍 t 分布的发现,说明在统计工作中要重视细微差别,要做细心谨慎 的统计人 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第三章 多元正态总体的统计推断 (一)目的与要求 1.了解几个常见的统计检验量服从的概率分布 2.理解样本统计量和根据显著性水平查表所得值之间的比较与最终接受 或拒绝原假设之间的关系。 3.掌握均值向量检验在实际经济研究中的应用,以及两总体及多总体均 值向量检验的应用意义。 4.理解协方差阵检验的应用意义,特别要学会两个检验结合运用 (二)教学内容 第二节 单个总体均值的推断 1.主要内容 均值向量的检验,HotellingT2分布及其性质,置信区域,联合置信区 间,均值向量的大样本推断 2.基本概念和知识点 HotellingT2 分布,置信区域,联合置信区间,均值向量的大样本推 断 3.问题与应用(能力要求) 理解交并原则,能推导总体协方差阵未知时的检验统计量;理解置信 区域与联合置信区间的关系;理解拉奥悖论 第三节 两个总体均值的比较推断 1.主要内容 两个独立样本情形及成对试验情形下的两个总体均值的比较推断 2.基本概念和知识点 总体协方差阵的联合无偏估计,成对试验

3.问题与应用(能力要求) 均值向量的假设检验与各分量的假设检验间的关系,掌握成对试验的 检验方法 第四节轮廓分析 1.主要内容 单总体轮廓分析,两总体轮廓分析 2,基本概念和知识点 轮廓 3.问题与应用(能力要求) 掌握轮廓分析在现实中的应用 第五节多个总体均值的比较检验(多元方差分析) 1.主要内容 多个总体均值的比较检验(多元方差分析),Wi1ksA分布及其性质 2.基本概念和知识点 多元方差分析,Wi1ksA分布 3.问题与应用(能力要求) 多元方差分析的同方差假定,Wi1ksA分布的性质 第六节协方差矩阵相等性的检验 1.主要内容 协方差矩阵相等性的检验 2.基本概念和知识点 博克斯M检验,似然比统计量 3.问题与应用(能力要求) 协方差阵检验的应用意义 第七节总体相关系数的检验 1.主要内容 总体相关系数的推断 2.基本概念和知识点 相关系数检验的检验统计量及其抽样分布 (三)思考与实践 理解置信区域与联合置信区间的关系:理解均值向量的假设检验与各分量的假 设检验间的关系:掌握单总体均值检验、多总体均值检验、轮廓分析、多元方差分析 等的检验方法 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 5
5 3.问题与应用(能力要求) 均值向量的假设检验与各分量的假设检验间的关系,掌握成对试验的 检验方法 第四节 轮廓分析 1.主要内容 单总体轮廓分析,两总体轮廓分析 2.基本概念和知识点 轮廓 3.问题与应用(能力要求) 掌握轮廓分析在现实中的应用 第五节 多个总体均值的比较检验(多元方差分析) 1.主要内容 多个总体均值的比较检验(多元方差分析),WilksΛ分布及其性质 2.基本概念和知识点 多元方差分析,WilksΛ分布 3.问题与应用(能力要求) 多元方差分析的同方差假定,WilksΛ分布的性质 第六节 协方差矩阵相等性的检验 1.主要内容 协方差矩阵相等性的检验 2.基本概念和知识点 博克斯 M 检验,似然比统计量 3.问题与应用(能力要求) 协方差阵检验的应用意义 第七节 总体相关系数的检验 1.主要内容 总体相关系数的推断 2.基本概念和知识点 相关系数检验的检验统计量及其抽样分布 (三)思考与实践 理解置信区域与联合置信区间的关系;理解均值向量的假设检验与各分量的假 设检验间的关系;掌握单总体均值检验、多总体均值检验、轮廓分析、多元方差分析 等的检验方法 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操

第四章判别分析 (一)目的与要求 1.了解判别分析的基本思想 2.掌握距离判别法、Bayes判别法、Fisher判别法。 3.理解逐步判别法对指标和样本的处理 (一)教学内容 第二节距离判别 1.主要内容 两组的距离判别,误判概率及估计,多组的距离判别 2.基本概念和知识点 线性判别函数,误判概率,交叉验证法 3.问题与应用(能力要求) 掌握不同情况下距离判别函数和判别规则,掌握交叉验证法估计误差 第三节贝叶斯判别 1.主要内容 最大后验概率法,最小期望误判代价法 2.基本概念和知识点 最大后验概率法,最小期望误判代价法 3.问题与应用(能力要求) 理解最大后验概率法和最小期望误判代价法的理论基础 第四节费希尔判别 1.主要内容 费希尔判别 2.基本概念和知识点 费希尔判别、费希尔第一判别函数、费希尔第二判别函数、费希尔第 i判别函数、贡献率 3.问题与应用(能力要求 费希尔判别的降维思想:费希尔判别函数间的关系 第五节逐步判别 1.主要内容 逐步判别法 2.基本概念和知识点 逐步判别法、附加信息检验、变量选择方法 3.问题与应用(能力要求)
6 第四章 判别分析 (一)目的与要求 1.了解判别分析的基本思想 2.掌握距离判别法、Bayes 判别法、Fisher 判别法。 3.理解逐步判别法对指标和样本的处理 (二)教学内容 第二节 距离判别 1.主要内容 两组的距离判别,误判概率及估计,多组的距离判别 2.基本概念和知识点 线性判别函数,误判概率,交叉验证法 3.问题与应用(能力要求) 掌握不同情况下距离判别函数和判别规则,掌握交叉验证法估计误差 第三节 贝叶斯判别 1.主要内容 最大后验概率法,最小期望误判代价法 2.基本概念和知识点 最大后验概率法,最小期望误判代价法 3.问题与应用(能力要求) 理解最大后验概率法和最小期望误判代价法的理论基础 第四节 费希尔判别 1.主要内容 费希尔判别 2.基本概念和知识点 费希尔判别、费希尔第一判别函数、费希尔第二判别函数、费希尔第 i 判别函数、贡献率 3. 问题与应用(能力要求) 费希尔判别的降维思想;费希尔判别函数间的关系 第五节 逐步判别 1.主要内容 逐步判别法 2.基本概念和知识点 逐步判别法、附加信息检验、变量选择方法 3. 问题与应用(能力要求)

逐步判别的应用 (三)思考与实践 不同判别分析法的适用情况 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第五章聚类分析 (一)目的与要求 1.理解各种距离和相似系数的意义和其各种定义计算方法下表现出来的 数量特征 2.理解R型和Q型聚类的区别和联系 3.样本间距离计算与聚类时类间距离的规定之间的关系: 4.掌握八种系统聚类法在实际应用中各自的特点和适应范围 (二)教学内容 第一节引言 1.主要内容 聚类分析的概念和分类 2.基本概念和知识点 聚类分析、R型聚类分析、Q型聚类分析 第二节距离和相似系数 1.主要内容 常用的距离和相似系数计算方法 2.基本概念和知识点 明氏距离、兰氏距离、马氏距离、斜交空间距离、夹角余弦、相关系 数 第三节系统聚类法 1.主要内容 系统聚类法 2.基本概念和知识点 最短距离法、最长距离法、类平均法、重心法、中间距离法、离差平 方和法、系统聚类法的统一、类的个数 3.问题与应用(能力要求) 掌握八种系统聚类法在实际应用中各自的特点和适应范围 第四节动态聚类法 1.主要内容
7 逐步判别的应用 (三)思考与实践 不同判别分析法的适用情况 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第五章 聚类分析 (一)目的与要求 1.理解各种距离和相似系数的意义和其各种定义计算方法下表现出来的 数量特征 2.理解 R 型和 Q 型聚类的区别和联系 3.样本间距离计算与聚类时类间距离的规定之间的关系; 4.掌握八种系统聚类法在实际应用中各自的特点和适应范围 (二)教学内容 第一节 引言 1.主要内容 聚类分析的概念和分类 2.基本概念和知识点 聚类分析、R 型聚类分析、Q 型聚类分析 第二节 距离和相似系数 1.主要内容 常用的距离和相似系数计算方法 2.基本概念和知识点 明氏距离、兰氏距离、马氏距离、斜交空间距离、夹角余弦、相关系 数 第三节 系统聚类法 1.主要内容 系统聚类法 2.基本概念和知识点 最短距离法、最长距离法、类平均法、重心法、中间距离法、离差平 方和法、系统聚类法的统一、类的个数 3. 问题与应用(能力要求) 掌握八种系统聚类法在实际应用中各自的特点和适应范围 第四节 动态聚类法 1.主要内容

动态聚类法 2.基本概念和知识点 k均值聚类分析 3.问题与应用(能力要求 k均值聚类的结果不唯一性 (三)思考与实践 全省旅游景点大数据的聚类分析。通过案例让学生了解文旅厅如何利用大数据 对传统的宏观旅游数据进行监测,政府部门对数据质量的要求不断提升。 (四)教学方法与毛段 课堂讲授、多媒体教学,上机实操 第六章主成分分析 (一)目的与要求 1.了解主成分的几何意义及其经济意义 2.理解原始指标的主成分与原始指标的关系及特性 3.熟悉主成分分析的适应范围,及其优缺点 4.掌握主成分个数确定的定性和定量方法 (二)教学内容 第一节引言 1.主要内容 主成分分析的基本概念 2.基本概念和知识点 降维、坐标轴转换 第二节总体的主成分 1,主要内容 总体主成分的计算与提取 2.基本概念和知识点 主成分、第ⅰ主成分、贡献率、累计贡献率、载荷 第三节样本的主成分 1.主要内容 样本主成分的计算与提取 2.基本概念和知识点 第ⅰ样本主成分、从S出发求主成分、从样本相关矩阵出发求主成分 3.问题与应用(能力要求) 时间序列的主成分分析、不同时期的主成分分析、综合评价的主成分
8 动态聚类法 2.基本概念和知识点 k 均值聚类分析 3. 问题与应用(能力要求) k 均值聚类的结果不唯一性 (三)思考与实践 全省旅游景点大数据的聚类分析。通过案例让学生了解文旅厅如何利用大数据 对传统的宏观旅游数据进行监测,政府部门对数据质量的要求不断提升。 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 第六章 主成分分析 (一)目的与要求 1.了解主成分的几何意义及其经济意义 2.理解原始指标的主成分与原始指标的关系及特性 3.熟悉主成分分析的适应范围,及其优缺点 4.掌握主成分个数确定的定性和定量方法 (二)教学内容 第一节 引言 1.主要内容 主成分分析的基本概念 2.基本概念和知识点 降维、坐标轴转换 第二节 总体的主成分 1.主要内容 总体主成分的计算与提取 2.基本概念和知识点 主成分、第 i 主成分、贡献率、累计贡献率、载荷 第三节 样本的主成分 1.主要内容 样本主成分的计算与提取 2.基本概念和知识点 第 i 样本主成分、从 S 出发求主成分、从样本相关矩阵出发求主成分 3. 问题与应用(能力要求) 时间序列的主成分分析、不同时期的主成分分析、综合评价的主成分
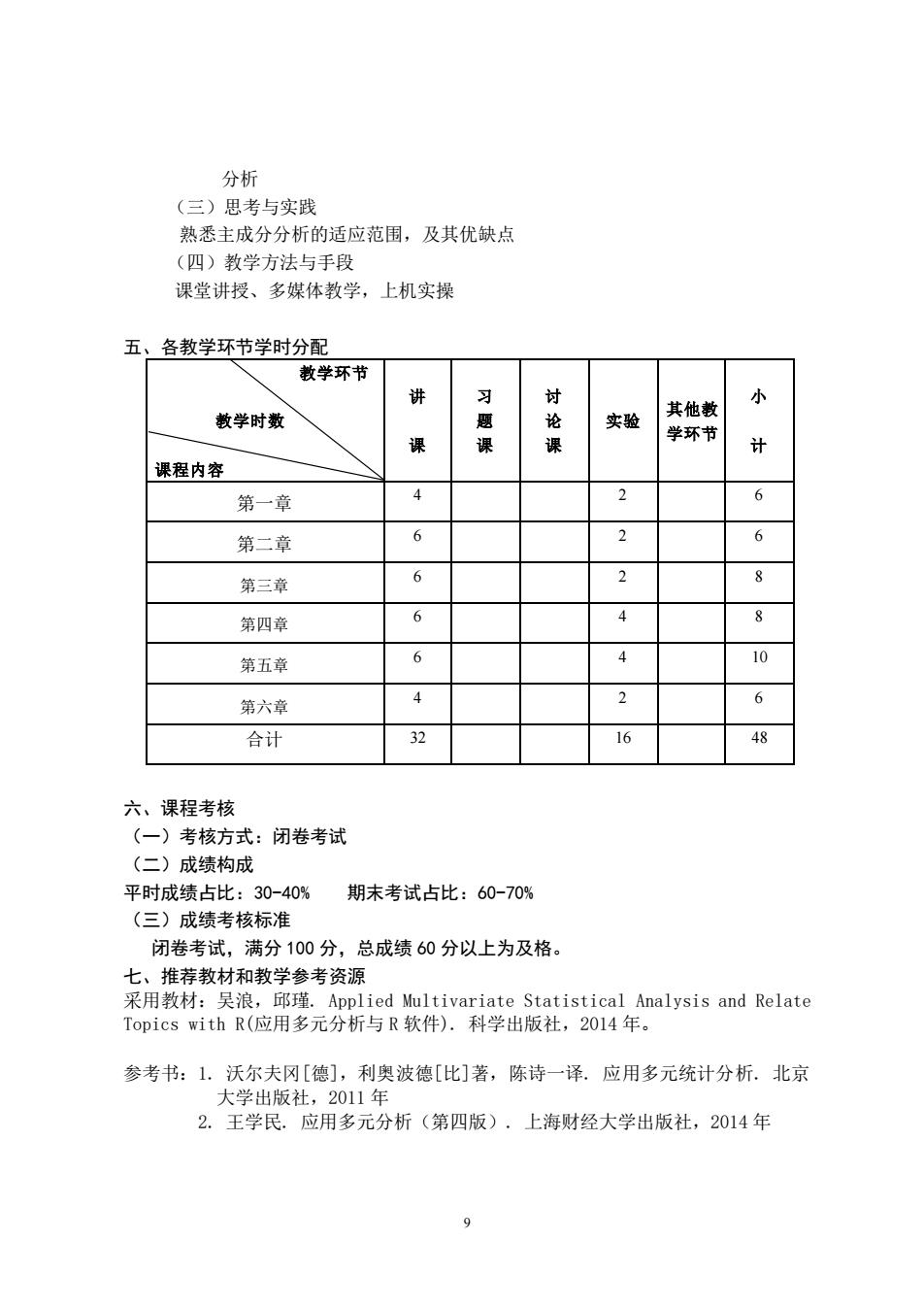
分析 (三)思考与实践 熟悉主成分分析的适应范围,及其优缺点 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 五、各教学环节学时分配 教学环节 习引 教学时数 题 实验 其他教 学环节 课 课程内容 第一章 4 第二章 第三章 第四章 6 第五章 4 10 第六章 合计 32 16 48 六、课程考核 (一)考核方式:闭卷考试 (二)成绩构成 平时成绩占比:30-40% 期末考试占比:60-70% (三)成绩考核标准 闭卷考试,满分100分,总成绩60分以上为及格。 七、推荐教材和教学参考资源 采用教材:吴浪,邱瑾.Applied Multivariate Statistical Analysis and Relate Topics with R(应用多元分析与R软件).科学出版社,2014年。 参考书:1.沃尔夫冈[德],利奥波德[比]著,陈诗一译.应用多元统计分析.北京 大学出版社,2011年 2.王学民.应用多元分析(第四版),上海财经大学出版社,2014年 9
9 分析 (三)思考与实践 熟悉主成分分析的适应范围,及其优缺点 (四)教学方法与手段 课堂讲授、多媒体教学,上机实操 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 4 2 6 第二章 6 2 6 第三章 6 2 8 第四章 6 4 8 第五章 6 4 10 第六章 4 2 6 合计 32 16 48 六、课程考核 (一)考核方式:闭卷考试 (二)成绩构成 平时成绩占比:30-40% 期末考试占比:60-70% (三)成绩考核标准 闭卷考试,满分 100 分,总成绩 60 分以上为及格。 七、推荐教材和教学参考资源 采用教材:吴浪,邱瑾. Applied Multivariate Statistical Analysis and Relate Topics with R(应用多元分析与 R 软件). 科学出版社,2014 年。 参考书:1. 沃尔夫冈[德],利奥波德[比]著,陈诗一译. 应用多元统计分析. 北京 大学出版社,2011 年 2. 王学民. 应用多元分析(第四版). 上海财经大学出版社,2014 年

3.何晓群.多元统计分析(第四版)·中国人民大学出版社,2015年 4.Richard A.Johnson[美],Dean W.Wichern[美]著,陆旋,叶俊译.实 用多元统计分析(第6版).清华大学出版社,2008年 八、其他说明 无 大纲修订人:周若榆 修订日期:2022-8-29 大纲审定人: 审定日期: 10
10 3. 何晓群. 多元统计分析(第四版). 中国人民大学出版社,2015 年 4. Richard A. Johnson[美],Dean W. Wichern[美]著, 陆旋,叶俊译. 实 用多元统计分析(第 6 版). 清华大学出版社,2008 年 八、其他说明 无 大纲修订人: 周若榆 修订日期:2022-8-29 大纲审定人: 审定日期: