
心号与素安 §8.9序列的傅里叶 变换(D737) 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §8.9 序列的傅里叶 变换(DTFT)
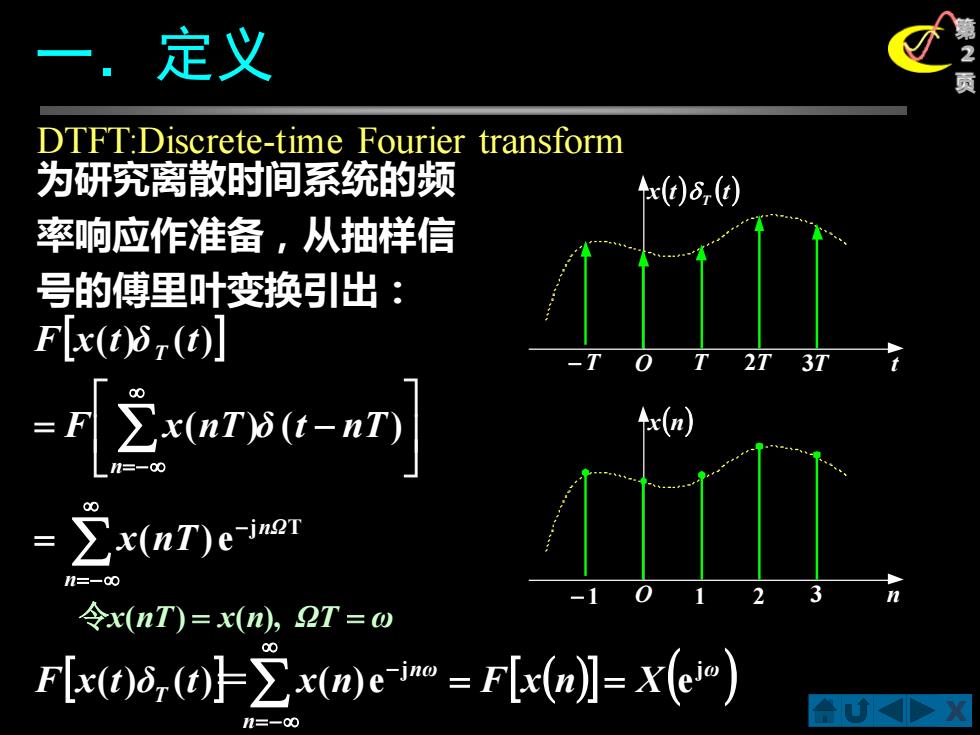
定义 DTFT:Discrete-time Fourier transform 为研究离散时间系统的频 ()5,() 率响应作准备,从抽样信 号的傅里叶变换引出: Fx(t)8,(t)] x(n) ∑x(nI)e-am 令x(nT)=x(n,2T=ω F[x0i,(H∑x(mew=F[x(nl=x(e) 合D
X 第 2 一.定义 页 − T O T 2T 3T t x(t) (t) T − 1 O 1 2 3 n x(n) =− − =− = = − n nΩ n T x nT F x nT δ t nT F x t δ t j T ( ) e ( ) ( ) ( ) ( ) 令x(nT) = x(n), ΩT = ω DTFT:Discrete-time Fourier transform 为研究离散时间系统的频 率响应作准备,从抽样信 号的傅里叶变换引出: ( ) ( ) ω n nω F x t δT t x n F x n X j j ( ) ( ) ( )e = = e =− = −

与z变换之关系 jIms jImz 单位圆 虚轴(s=jo) (=ei) 1⊙ +1 Res Rez x)=2k =。● 令z=ej°,z=1,即单位圆上的变换 周期为 xeo)=X(a 2π
X 第 3 与 页 z变换之关系 ( ) ( ) ω z ω X X z j e j e = = ( ) ( ) =− − = n n X z x n z 令z = e jω , z = 1,即单位圆上的z变 换 2 周期为 Re s jIm s O 虚轴(s = j) Re z jIm z O + 1 ( e ) j z = 单位圆

逆变换 网=手x"d: =手e)eim.ede) )e.ejedo ")do 表示 DTPT[lx(l=xe)-∑x(me-do IDTFr[x(x()=x(e)ei do
X 第 4 逆变换 页 ( ) ( ) ( ) ( ) ( ) X( ) ω X ω π X π x n X z z z ω nω ω nω ω ω ω nω ω ω z n z e e d 2π 1 e e e je d 2 j 1 e e e d e 2 j 1 d 2π j 1 π π j j π π j j j j j j j j 1 1 1 − − − − = − = = = = = ( ) ( ) ( ) X( ) x(n) X( ) ω x n X x n ω ω ω nω n ω nω e e d 2 π 1 IDTFT e DTFT e e d π π j j j j j − =− − = = = = 表示

二 傅氏变换、拉氏变换、变换的关系 1.三种变换的比较 2频率的比较 3.s平面虚轴上的拉氏变换即为傅氏变换 4.z平面单位圆上的z变换即为序列的傅氏变换 (DTFT
X 第 5 二.傅氏变换、拉氏变换、z变换的关系页 1. 三种变换的比较 2.频率的比较 3.s平面虚轴上的拉氏变换即为傅氏变换 4.z平面单位圆上的z变换即为序列的傅氏变换 (DTFT)

1.三种变换的比较 变换名称 傅里叶变 拉普拉斯 变换 换 变换 信号类型 连续信号 离散信号 x() x(nT) 变量 j2 S=0+j2 t=esT
X 第 6 1.三种变换的比较 页 x(t) 连续信号 x(nT) 离散信号 jΩ s =σ + jΩ sT z = e 变换名称 傅里叶变 换 拉普拉斯 变换 z变换 信号类型 变量

拉氏变换 z变换 x6付)=∑(nr).ewr x)=Σxm)x s=j2, 2T=0, 傅氏变换 nT-→n 对于离散序列x(n xe)=∑xae 合U
X第7页 对于离散序列 x (n ): ( ) ( ) =− − = n snT Xs s x nT e 拉氏变换 ⎯⎯→⎯→= nT nz sT e , ( ) ( ) =− − = n n X z x n z z变 换= ω z j e ⎯⎯→⎯→ = = nT n T s j , , ( ) ( ) =− − = n ω n ω X x n j j e e 傅氏变换

2.频率的比较 模拟角频率2,量纲:弧度/秒; 数字角频率0ω,量纲:弧度: e是周期为 的周期函数 关系:w=2T
X 第 8 页 2.频率的比较 模拟角频率 ,量纲:弧度/秒; 数字角频率 ,量纲:弧度; 是周期为 的周期函数 关系: Ω ω ω =ΩT jω e 2π

3.s平面虚轴上的拉氏变换即为傅氏变换忍 0=0,S=j2 H(i)=H(s) 4.z平面单位圆上的z变换即为序列的傅氏 变换(DTFT) =1,=ei x(jo)=X()
X 第 9 3. 页 s平面虚轴上的拉氏变换即为傅氏变换 σ = 0,s = jΩ ( ) ( ) s Ω H Ω H s j j = = 4. z平面单位圆上的z变换即为序列的傅氏 变换(DTFT) ω z z j = 1, = e ( ) ( ) ω z X ω X z j e j = =