
心号与素婴 §8.8离散系统的系统品数 单位样值响应与系统函数 ·系统函数的零极点分布对系统特性的影响 确定单位样值响应 稳定性 因果性 新疆大学信息科学与工程学院电子系 2003.1 退出 开脸
新疆大学信息科学与工程学院电子系 2003.1 §8.8 离散系统的系统函数 •单位样值响应与系统函数 •系统函数的零极点分布对系统特性的影响 确定单位样值响应 稳定性 因果性

一.单位样值响应与系统函数 1定义 M Ha)= Y) 2.h(m和Hz)为一对z变换对 zn(n)]=H(e)
X 第 2 一.单位样值响应与系统函数 页 1.定义 2. h(n)和H(z)为一对z变换对 ( ) ( ) ( ) = − = − = = N k k k M r r r a z b z X z Y z H z 0 0 Zh(n)= H(z)

1. 定义 线性时不变离散系统由线性常系 激励为因果序列 数差分方程描述,一般形式为 x(1)=x(2)==0 ∑atn-)-∑3,x-r) 系统处于零状态 上式两边取变换得 (1)=y(2)==0 r(m:-x( H(:)与系统的差分方 所以)= ∑bx 程的系数、结构有关 r= 描述了系统的特性。 H():离散时间系统的系统函数
X 第 3 页 ( ) ( ) = = − = − M r r N k k a y n k b x n r 0 0 1.定义 线性时不变离散系统由线性常系 数差分方程描述,一般形式为 ( ) ( )= − = − = M r r r N k k k Y z a z X z b z 0 0 ( ) ( ) ( ) = − = − = = N k k k M r r r a z b z X z Y z H z 0 0 所 以 x(−1) = x(− 2) == 0 y(−1) = y(− 2) == 0 激励为因果序列 系统处于零状态 上式两边取z变换得 只与系统的差分方 程的系数、结构有关, 描述了系统的特性。 H(z) H(z) : 离散时间系统的系统函数

2.h(n)和H(z)为一对z变换 δ(nd h(n) 系统 若x(n)=n则x(a)=1 zin(n)]=H(e) ·由H(a求n:(n=Z[Ha】 系统的零状态响应: ()=n(n)*x()Y(z)=H(z)-x(E) 创题 合U>风
X 第 4 2. h(n)和H(z)为一对z变换 页 若x(n) = δ(n),则X(z) = 1 Zh(n)= H(z) y (n) = h(n) x(n)Y(z) = H(z) X(z) zs ●系统的零状态响应: H(z) h(n) h(n) Z H(z) 1 : − ● 由 求 = 系 统 (n) h(n)

二. 系统函数的零极点分布对系统特性的影 因为(n)H(z),所以可以从WH(z)的零极点分布情况 确定单位样值响应(n)的特性 1.由零极点分布确定单位样值响应 2.离散系统的稳定性 3.系统的因果性
X 第 5 二.系统函数的零极点分布对系统特性的影响页 1.由零极点分布确定单位样值响应 2.离散系统的稳定性 3.系统的因果性 ( ) ( ) ( ) 确定单位样值响应 ( )的特性 因 为 ,所以可以从 的零极点分布情况, h n h n H z H z

1.由零极点分布确定单位样值响应 h:r 立0-,x H 乙,:零点 2* it-n.x) 1 极点 展成部分分式:(假设无重根) )= 4=4+ K=0-Pk k=1-Pk 因为 h() 所uw-A+空}4空网 合U
X 第 6 1.由零极点分布确定单位样值响应 页 ( ) ( ) = − = − − − = N k k M r r p z z z G 1 1 1 1 1 1 ( ) = − = − = N k k k M r r r a z b z H z 0 0 极点 零点 : : k r p z 展成部分分式:(假设无重根) ( ) = = − = + − = N k k k N k k k z p A z A z p A z H z 1 0 0 ( ) − = += − N k k k z p A z h n Z A 1 0 1 所 以 因为 h(n) H(z) ( ) ( ) ( ) = = + N k n A n Ak pk u n 1 0

由零极点分布确定单位样值响应(续) n=A,n)+∑A(pyu(n) k=1 P:的极点,可以是不同的实数或共轭复数 决定了(的特性。其规律可能是指数衰减、上升, 或为减幅、增幅、等幅振荡。 A0,Ak:与H(z)的零点、极点分布都有关
X 第 7 页 ( ) ( ) ( ) ( ) = = + N k n h n A δ n Ak pk u n 1 0 的极点,可以是不同的实数或共轭复数, 决定了 的特性。其规律可能是指数衰减、上升, 或为减幅、增幅、等幅振荡。 p H(z) k : h(n) A0 , Ak :与H(z)的零点、极点分布都有关。 由零极点分布确定单位样值响应(续)
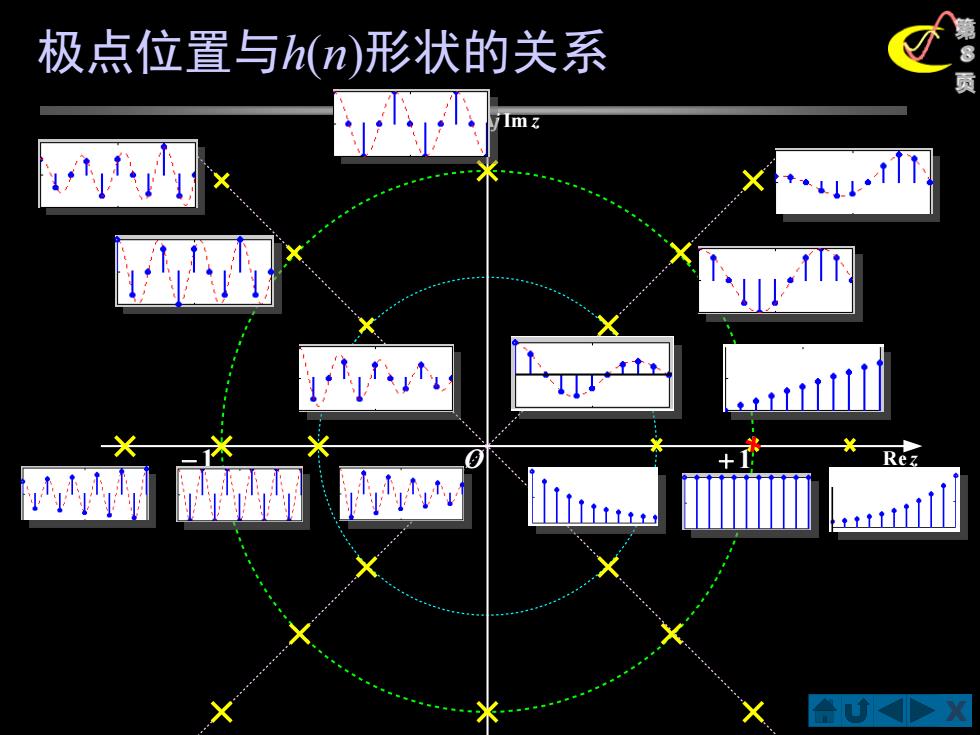
极点位置与h(n)形状的关系 TIT-411 Re
X 第 8 页 O R e z jIm z − 1 + 1 极点位置与h(n)形状的关系

利用z~s平面的映射关系 s平面 平面 极点位置 h(@特点 极点位置 h(n)特点 虚轴上 等幅 单位圆上 等幅 原点时 u(t) 0=0 z=1 u(n) z-1 左半平面 衰减 单位圆内 减幅 右半平面 增幅 单位圆外 增幅 合心>
X 第 9 页 s平面 z平面 极点位置 h(t)特点 极点位置 h(n)特点 虚轴上 等幅 单位圆上 等幅 原点时 左半平面 衰减 单位圆内 减幅 右半平面 增幅 单位圆外 增幅 ( ) s u t 1 θ = 0 ( ) − 1 z z u n 利用z~s平面的映射关系 z = 1

2.离散系统的稳定性 (1)定义:对于稳定系统,只要输入是有界的,输出必 定是有界的(BBO)。 (2)稳定性判据 判据1:离散系统稳定的充要条件:单位样值响应绝对 可和。 Σa)a,a<1
X 第 10 2.离散系统的稳定性 页 ( ) n=− h n 对于稳定系统,只要输入是有界的,输出必 定是有界的(BIBO)。 (2)稳定性判据 (1)定义: 判据1:离散系统稳定的充要条件:单位样值响应绝对 可和。 判据2:对于因果系统,其稳定的充要条件为: H(z)的全部极点应落在单位圆之内。即收敛域应包括单 位圆在内: z a, a 1