
心号与系要 §8.6z变换与拉普拉斯变换 的关系 米 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §8.6 z变换与拉普拉斯变换 的关系
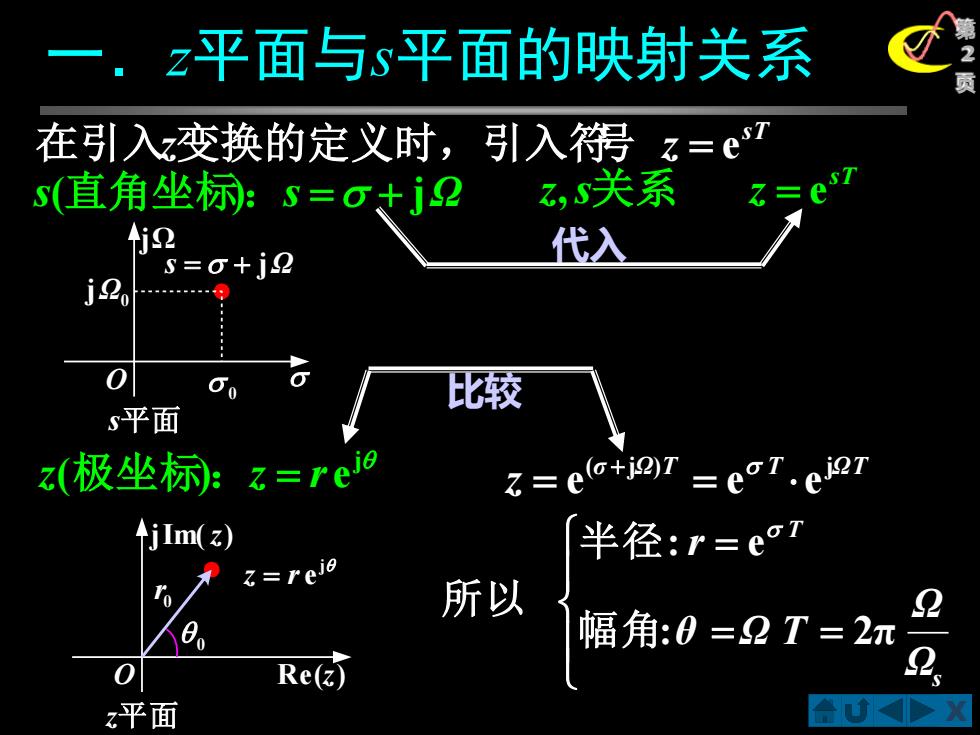
一,z平面与s平面的映射关系 在引入x变换的定义时,引入等z=e7 s(直角坐标:S=otj2 乙,s关系2=e s=o+jQ 代入 0 00 比较 s平面 z(极坐标: z=reio e27 jIm() 半径:r=eo7 所以 幅角:0=2T=2π Re( 2 平面
X 第 2 页 sT z,s关系 z = e σ Ω T T ΩT z ( j ) j = e = e e + = = = s T Ω Ω θ Ω T r : 2π : e 幅 角 半 径 所 以 代入 比较 一.z平面与s平面的映射关系 s T 在引入z变换的定义时,引入符号 z = e s(直角坐标):s = + jΩ O jΩ 0 jΩ 0 s = + jΩ s平面 j z(极坐标):z = r e j z = r e Re(z) jIm(z) O z平 面 0 r 0

几种情况 (1) s平面的原点 0=0 平面 即 (2) 2=0 0=0 s平面 g0 o为常数:-0→+0 左半平面 虚轴 右半平面 左向右移 平面 r1 r为常数:0→+o 单位圆内 单位圆上 单位圆外 半径扩大 (3)s平面2=0:实轴→z平面0=0,正实轴 (4)?~s映射不是单值的。2=± →0=π 演示 演示 2
X 第 3 页 s平面 z平面 几种情况 (1)s平面的原点 ,z平面 ,即 。 = = 0 0 Ω σ = = 0 1 θ r z = 1 σ 0 σ = 0 σ 0 为常数: −→ + r 1 r = 1 r 1 r为常数: 0 → + 左半平面 虚轴 右半平面 左向右移 单位圆内 单位圆上 单位圆外 半径扩大 (2) (3) s平 面Ω= 0:实轴→ z平 面θ = 0,正实轴 (4)z~s映射不是单值的。 π 2 s = →θ = Ω Ω

二,z变换与拉式变换表达式之对应 x(t) 均匀抽样→x(,[x】=X(s) z[x(n)]=x(2) 能否借助r(s写出X(3)? 注意: 连续时间信号的突变点函数值与对应的序列样值有区别。 例如,阶跃信号)在t=0点定义为: 阶跃序列(n在点n=0定义 若连续时间信(⑦由N项指数信号相加组合成 0=,(d)+e,d)++(d ∑,0=立4e0
X 第 4 二. 页 z变换与拉式变换表达式之对应 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )? , X s X z x t x n L x t X s Z x n X z 能否借助 写 出 ⎯均匀抽 样 ⎯ ⎯→ = , = ( ) ( ) 0 1 ; 2 1 0 阶跃序列 在 点 定义为 例如,阶跃信号 在 点定义为 = = u n n u t t 若连续时间信号x ˆ(t)由N项指数信号相加组合而成 x(t) x (t) x (t) x (t) n ˆ ˆ ˆ ˆ = 1 + 2 ++ x (t) A u(t) N i p t i N i i i = = = = 1 1 ˆ e 注意: 连续时间信号的突变点函数值与对应的序列样值有区别

容易求得,它的拉式变换为 名, 若序(nT由N项指数序列相加组合成 x(nT)=x(aT)+x2(nT)++x(nT) -xr)-4e"w 它的z变换为 借助模拟滤波器 设计数字滤波器 =1 倒题 倒题注意跳变值
X 第 5 页 容易求得,它的拉式变换为 ( ) = − = N i i i s p A L x t 1 ˆ 若序列x(nT)由N项指数序列相加组合而成 x(nT) x (nT) x (nT) x (nT) = 1 + 2 ++ N x (nT) A u(nT) N i p nT i N i i i = = = = 1 1 e 它的z变换为 ( ) = − − = N i p T i z A Z x nT i 1 1 1 e 注意跳变值 借助模拟滤波器 设计数字滤波器

注意跳变值 (t0) A:epim (t>0) 按抽样规律建立二者繇时必须点补足4,即 档n≠0) x,(nT)u(n)=
X 第 6 注意跳变值 页 ( ) ( ) ( ) ( ) = = e 0 0 2 0 0 ˆ A t t A t x t p t i i i i ( ) ( ) ( ) ( ) = = e 0 0 0 0 A t A t t x nT p nt i i i i 按抽样规律建立二者联系时必须在 点补足 ,即2 0 Ai ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = + = = 0 2 ˆ ˆ 0 A n t nT x t u t n t nT x t u t x nT u n i i i i 当 当