
第三章资金时间价值 资金时间价值 资金时间价值是指资金在扩大再生产及其 循环周转过程中,随着时间变化而产生的增 值。 等额货币在不同时点上具有不同的价值
第三章 资金时间价值 一、资金时间价值 ⚫ 资金时间价值是指资金在扩大再生产及其 循环周转过程中,随着时间变化而产生的增 值。 ⚫ 等额货币在不同时点上具有不同的价值

二、时间价值的表示形式一利息与利率 1.利息:占用资金所付出的代价(或放弃使 用资金所得的的补偿)。 Fn=P+In 其中:Fn一本利和;P一本金; I一利息; n一计算利息的周期数 利率:在一个计息周期内所得到的利 息额与借贷金额之比。 i=IP×100% 其中:I一一个计息周期的利息
二、时间价值的表示形式—利息与利率 1.利息:占用资金所付出的代价(或放弃使 用资金所得的的补偿)。 Fn=P+ In 其中:Fn-本利和;P-本金; In-利息; n-计算利息的周期数。 利率:在一个计息周期内所得到的利 息额与借贷金额之比。 i= I1 /P×100% 其中:I1-一个计息周期的利息

2.单利和复利 (1)单利(Simple Interest):仅用本金计算利 息,利息不再生利息。 Im=P×n×i n个计息周期后本利和: Fm=P+In=P(1+i×n) (2)复利(Compound Interest): 以本金与累 计利息之和为基数计算利息,即利上加利。 Fn=P×(1+i)
2.单利和复利 (1)单利(Simple Interest):仅用本金计算利 息,利息不再生利息。 In =P×n×i n个计息周期后本利和: Fn=P+ In=P(1+i×n) (2)复利(Compound Interest):以本金与累 计利息之和为基数计算利息,即利上加利。 Fn =P× (1+i)n

3.名义利率和实际利率 1)名义利率:计息周期的利率乘以每年的 息周期数。 (2)实际利率: 每年的计息周期数用复利计 息所得到的年利率 两者的关系:设名义利率为, 一年中计息姿 为m,则一个计息周期的利率应为r/m。 年实际利率: i=(1+r/m)m 当m=1时,i=r, 即名义利率等于实际利率; 当m>1时, i>r, 即名义利率小于实际利率; 当m无穷时,i=er一1
3.名义利率和实际利率 (1)名义利率:计息周期的利率乘以每年的计 息周期数。 (2) 实际利率:每年的计息周期数用复利计 息所得到的年利率。 两者的关系:设名义利率为r,一年中计息数 为m,则一个计息周期的利率应为r/m。 年实际利率: i=(1+r/m)m—1 当 m=1时, i=r,即名义利率等于实际利率; 当 m>1时, i>r,即名义利率小于实际利率; 当 m→无穷时,i=e r—1

例: 若年名义利率为30%, 每季复利一次, 问年实际利率为多少? 解: r=30%, =4, i实=(1+r/m)m-1=(1+30%/4)4一1=33.55%
例: 若年名义利率为30%,每季复利一次, 问年实际利率为多少? 解: r=30%, m=4, i 实=(1+r/m)m-1=(1+30%/4)4-1=33.55%

三、现金流量图与资金等值的概念 1.资金等值的概念 资金等值:在考虑资金时间价值因素后,不同 时点上数额不等的资金在一定利率条件下具有 相等的价值 2.影响资金等值的因素有三个:资金额大小、 资金发生的时间和利率,它们构成资金等值的三 要素 3,利用等值概念,将一个时点发生的资金金额 换算成另一时点的等值金额,这一过程叫资金等 值换算
三、现金流量图与资金等值的概念 1.资金等值的概念 资金等值:在考虑资金时间价值因素后,不同 时点上数额不等的资金在一定利率条件下具有 相等的价值。 2.影响资金等值的因素有三个:资金额大小、 资金发生的时间和利率,它们构成资金等值的三 要素。 3.利用等值概念,将一个时点发生的资金金额 换算成另一时点的等值金额,这一过程叫资金等 值换算

>贴现与贴现率:把将来某一时点的资金金额换算 成现在时点的等值金额称为贴现或折现。贴现时 所用的利率称贴现率或折现率 >现值:现值是指资金“现在”的价值。 注意 “现值”是一个相对的概念,一 般地说,将t十k时 点上发生的资金折现到第t个时点,所得的等值金 额就是第t十k个时点上资金金额在时点的现值 现值用符号P表示. >终值:终值是现值在未来时点上的等值资金,用 符号F表示。 >等年值:等年值是指分期等额收支的资金值,用 符号A表示
➢贴现与贴现率:把将来某一时点的资金金额换算 成现在时点的等值金额称为贴现或折现。贴现时 所用的利率称贴现率或折现率。 ➢现值:现值是指资金“现在”的价值。注意 “现值”是一个相对的概念,一般地说,将t+k时 点上发生的资金折现到第t个时点,所得的等值金 额就是第t+k个时点上资金金额在t时点的现值, 现值用符号P表示。 ➢终值:终值是现值在未来时点上的等值资金,用 符号F表示。 ➢等年值:等年值是指分期等额收支的资金值,用 符号A表示
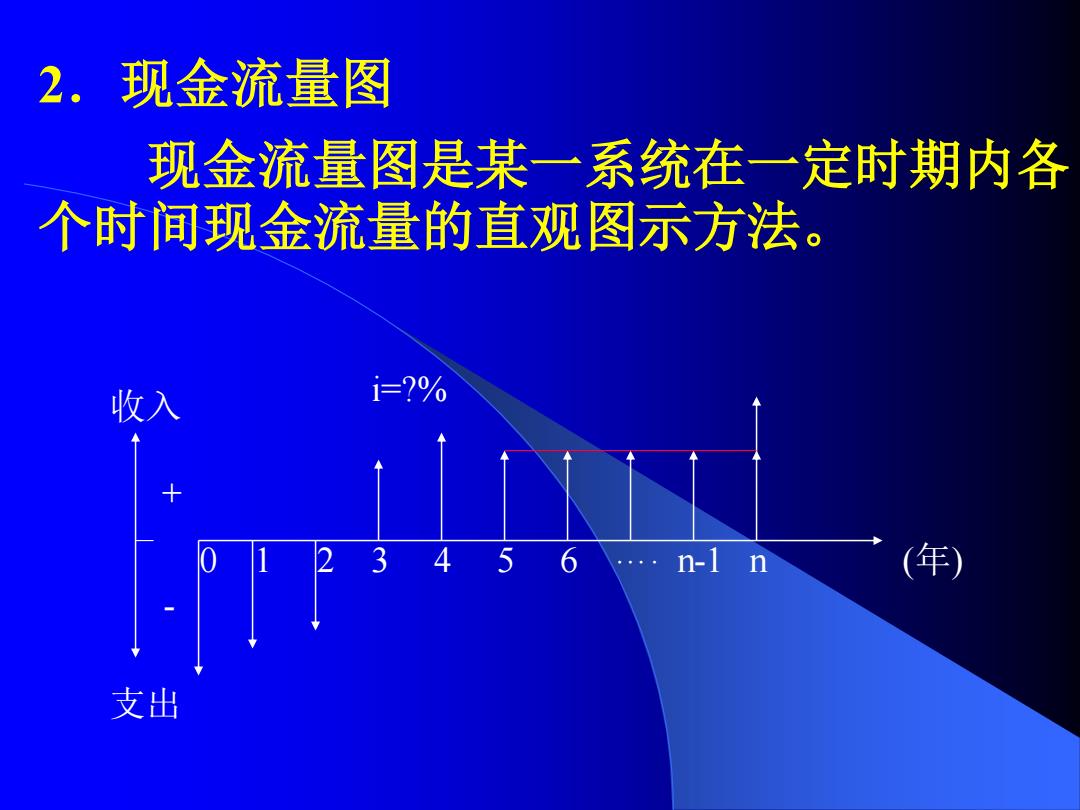
2.现金流量图 现金流量图是某一系统在一定时期内各 个时间现金流量的直观图示方法。 收入 i=?% 3 456…n-1 n (年 支出
2.现金流量图 现金流量图是某一系统在一定时期内各 个时间现金流量的直观图示方法。 + - 收入 支出 0 1 2 3 4 5 6 …. n-1 n (年) i=?%

画法: >先作一水平线为时间坐标(横坐标), 按单位时间 分段(等分),自左向右为时间的递增,表示时间 的历程。时间一般以年为单位,用0,1,2, 3, 表示。在分段点所定的时间通常表示该 时点末(一般表示为年末),同时也表示为下一个 时点初(下一年的年初,如上图中,时点1表示第 1年的年末或第2年的年初 >垂直线表示时点上系统所发生的现金流量,即 实际收益或费用的情况,其中箭头向下表示现金 流出(费用),向上则表示现金流入(收益), 线段的 长度代表发生的金大小,按比例画出
画法: ➢先作一水平线为时间坐标(横坐标),按单位时间 分段(等分),自左向右为时间的递增,表示时间 的历程。时间一般以年为单位,用 0,1,2, 3,…,n表示。在分段点所定的时间通常表示该 时点末(一般表示为年末),同时也表示为下一个 时点初(下一年的年初),如上图中,时点1表示第 1年的年末或第2年的年初。 ➢垂直线表示时点上系统所发生的现金流量,即 实际收益或费用的情况,其中箭头向下表示现金 流出(费用),向上则表示现金流入(收益),线段的 长度代表发生的金额大小,按比例画出

>利率标注于水平线上方。为计算方便,常将上 述现金流入与现金流出所发生的具体时间假定在 期初(年初)或期末(年末)。例如将项目投资假定在 年初发生,而将逐年所发生的经营成本(费用)、 销售收入(收益)均假定在年末发生 注意:现金流量图与选择的对象有关
➢利率标注于水平线上方。为计算方便,常将上 述现金流入与现金流出所发生的具体时间假定在 期初(年初)或期末(年末)。例如将项目投资假定在 年初发生,而将逐年所发生的经营成本(费用)、 销售收入(收益)均假定在年末发生。 注意:现金流量图与选择的对象有关