
第六章 轮系
第六章 轮系

§6-1 轮系及其分类 轮系是由一系列齿轮所组成的传动装置。 定义:这种由一系列齿轮组成的传动系统称为 轮系。 它通常介于原动机和执行机构之间,把原动机 的运动和动力传给执行机构。 工程实际中常用其实现变速、换向和大功率传 动等,具有非常广泛的应用。 轮系的类型 定轴轮系 周转轮系 混合轮系
§6-1 轮系及其分类 轮系是由一系列齿轮所组成的传动装置。 定义:这种由一系列齿轮组成的传动系统称为 轮系。 它通常介于原动机和执行机构之间,把原动机 的运动和动力传给执行机构。 工程实际中常用其实现变速、换向和大功率传 动等,具有非常广泛的应用。 轮系的类型 定轴轮系 周转轮系 混合轮系
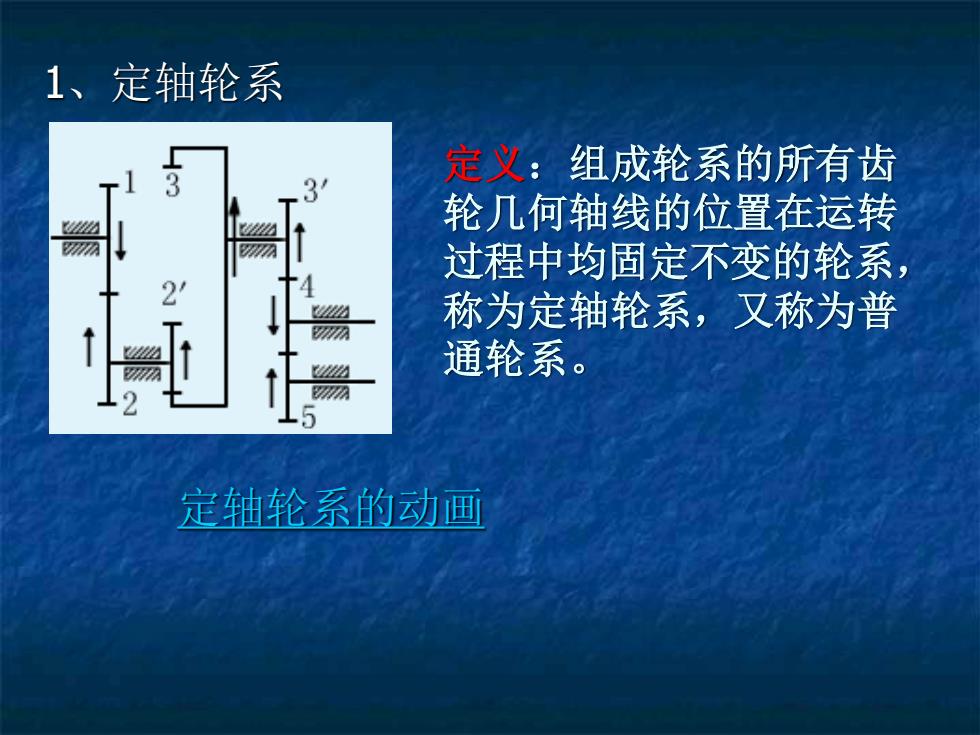
1、定轴轮系 定义:组成轮系的所有齿 轮几何轴线的位置在运转 过程中均固定不变的轮系, 称为定轴轮系,又称为普 通轮系。 定轴轮系的动画
1、定轴轮系 定义:组成轮系的所有齿 轮几何轴线的位置在运转 过程中均固定不变的轮系, 称为定轴轮系,又称为普 通轮系。 定轴轮系的动画
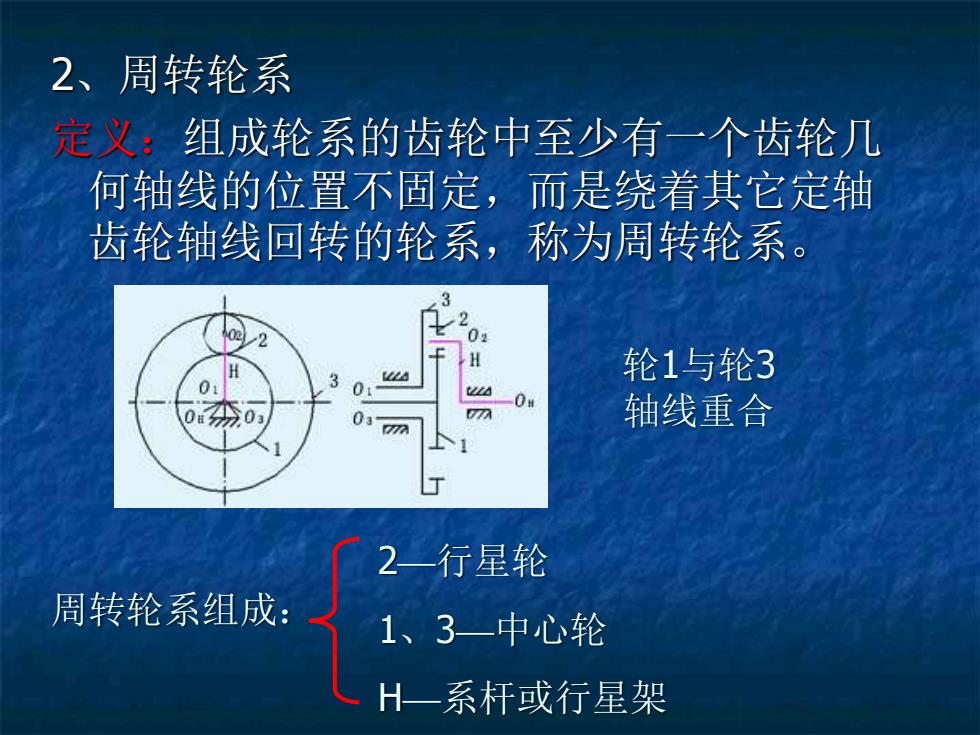
2、周转轮系 定义:组成轮系的齿轮中至少有一个齿轮几 何轴线的位置不固定,而是绕着其它定轴 齿轮轴线回转的轮系,称为周转轮系。 周转轮系组成: 2—行星轮 1、3—中心轮 H—系杆或行星架 轮1与轮3 轴线重合
2、周转轮系 定义:组成轮系的齿轮中至少有一个齿轮几 何轴线的位置不固定,而是绕着其它定轴 齿轮轴线回转的轮系,称为周转轮系。 周转轮系组成: 2—行星轮 1、3—中心轮 H—系杆或行星架 轮1与轮3 轴线重合

周转轮系的分类 1. 根据周转轮系所具有的自由度数目不同 (1)行星轮系 周转轮系中,若将中心轮3(或1)固定,则整 个轮系的自由度为1。这种自由度为1的周转轮 系称为行星轮系。为了确定该轮系的运动,只需 要给定轮系中一个构件以独立的运动规律即可。 (2)差动轮系 周转轮系中,若中心轮1和3均不固定,则整个 轮系的自由度为2。这种自由度为2的周转轮系 称为差动轮系。为了使其具有确定的运动,需要 两个原动件
周转轮系的分类 1. 根据周转轮系所具有的自由度数目不同 (1)行星轮系 周转轮系中,若将中心轮3(或1)固定,则整 个轮系的自由度为1。这种自由度为1的周转轮 系称为行星轮系。为了确定该轮系的运动,只需 要给定轮系中一个构件以独立的运动规律即可。 (2)差动轮系 周转轮系中,若中心轮1和3均不固定,则整个 轮系的自由度为2。这种自由度为2的周转轮系 称为差动轮系。为了使其具有确定的运动,需要 两个原动件
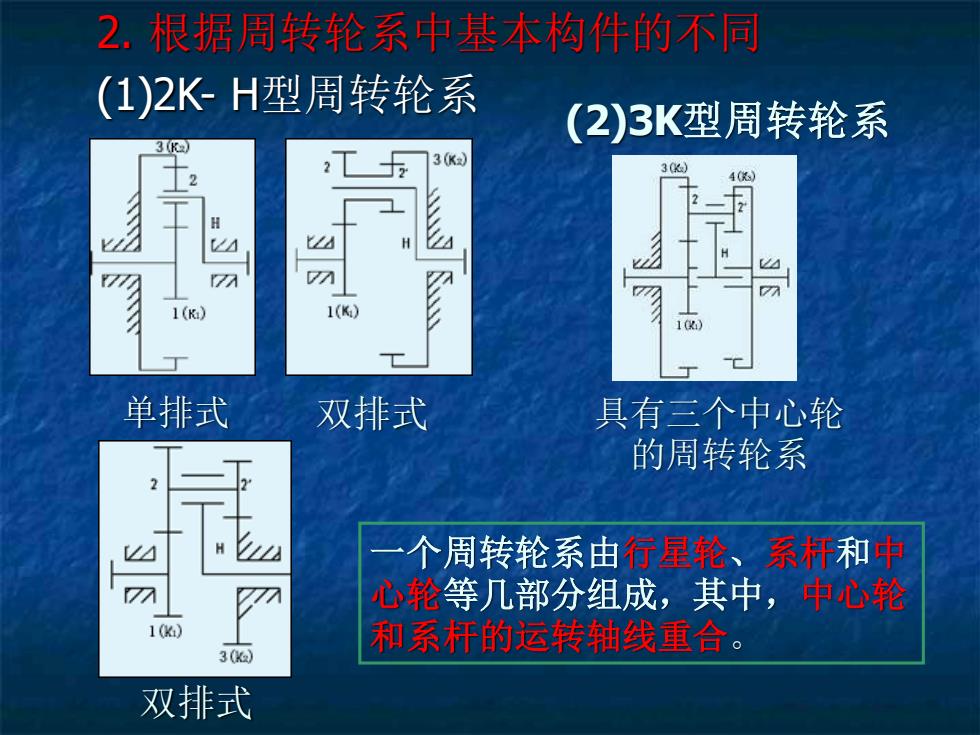
2. 根据周转轮系中基本构件的不同 (1)2K- H型周转轮系 单排式 双排式 双排式 (2)3K型周转轮系 具有三个中心轮 的周转轮系 一个周转轮系由行星轮、系杆和中 心轮等几部分组成,其中,中心轮 和系杆的运转轴线重合
2. 根据周转轮系中基本构件的不同 (1)2K- H型周转轮系 单排式 双排式 双排式 (2)3K型周转轮系 具有三个中心轮 的周转轮系 一个周转轮系由行星轮、系杆和中 心轮等几部分组成,其中,中心轮 和系杆的运转轴线重合

§6-2 定轴轮系的传动比 1、传动比定义 轮系中输入轴的角速度(或转速)与输出轴的 角速度(或转速)之比,即: 2、一对齿轮的传动比 1 2 2 1 12 z z i = = 正号:表示转向相同,用于内啮合 负号:表示转向相反,用于外啮合
§6-2 定轴轮系的传动比 1、传动比定义 轮系中输入轴的角速度(或转速)与输出轴的 角速度(或转速)之比,即: 2、一对齿轮的传动比 1 2 2 1 12 z z i = = 正号:表示转向相同,用于内啮合 负号:表示转向相反,用于外啮合
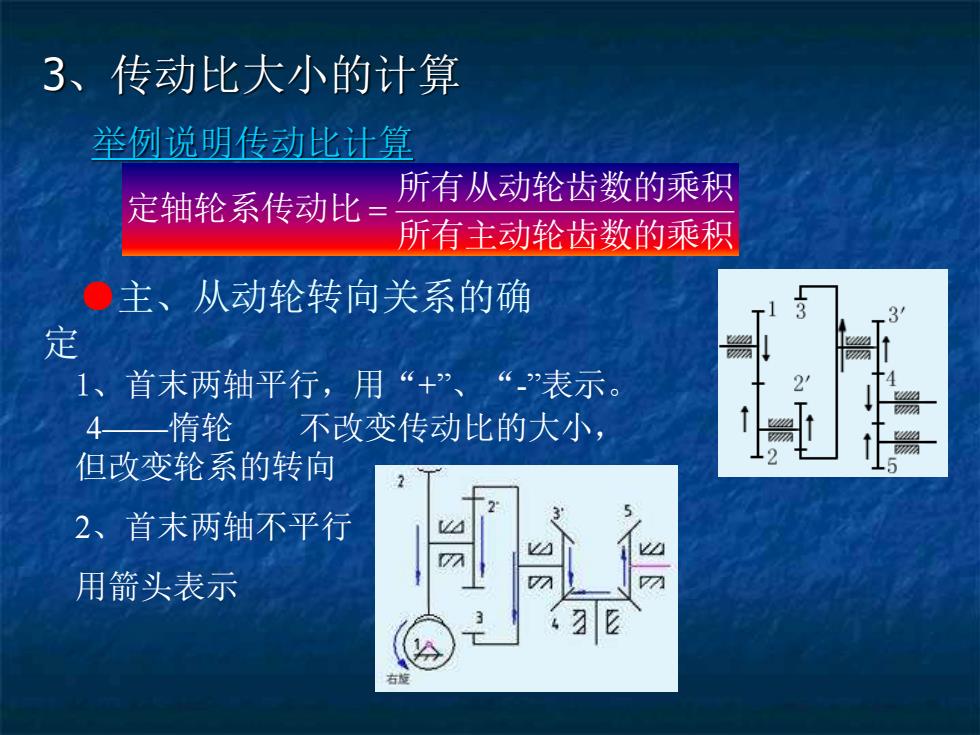
3、传动比大小的计算 举例说明传动比计算 ●主、从动轮转向关系的确 定 1、首末两轴平行,用“+”、 “-”表示。 4——惰轮 不改变传动比的大小, 但改变轮系的转向 2、首末两轴不平行 用箭头表示 所有主动轮齿数的乘积 所有从动轮齿数的乘积 定轴轮系传动比 =
3、传动比大小的计算 举例说明传动比计算 ●主、从动轮转向关系的确 定 1、首末两轴平行,用“+”、 “-”表示。 4——惰轮 不改变传动比的大小, 但改变轮系的转向 2、首末两轴不平行 用箭头表示 所有主动轮齿数的乘积 所有从动轮齿数的乘积 定轴轮系传动比 =

3、所有轴线都平行 所有主动轮齿数的乘积 m 所有从动轮齿数的乘积 i ( 1) 5 1 = = − m——外啮合的次数 4、所有齿轮的几何轴线不都平行,但首、尾两轮的轴 线互相平行 仍可在传动比的计算结果中加上"+"、 "-"号来表示主、 从动轮的转向关系
3、所有轴线都平行 所有主动轮齿数的乘积 m 所有从动轮齿数的乘积 i ( 1) 5 1 = = − m——外啮合的次数 4、所有齿轮的几何轴线不都平行,但首、尾两轮的轴 线互相平行 仍可在传动比的计算结果中加上"+"、 "-"号来表示主、 从动轮的转向关系

§6-3 周转轮系传动比 反转法 假想给整个轮系加上一 个公共的角速度(-H ), 据相对运动原理,各构 件之间的相对运动关系 并不改变,但此时系杆 的角速度就变成了H -H=0,即系杆可视为静止不动。于 是,周转轮系就转化成了一个假想的定轴轮系,通常称这 个假想的定轴轮系为周转轮系的转化机构。 以单排2K-H型周转轮系为例 1 3 3 1 3 1 1 3 ( 1) Z Z i H H H H H = − − − = =
§6-3 周转轮系传动比 反转法 假想给整个轮系加上一 个公共的角速度(-H ), 据相对运动原理,各构 件之间的相对运动关系 并不改变,但此时系杆 的角速度就变成了H -H=0,即系杆可视为静止不动。于 是,周转轮系就转化成了一个假想的定轴轮系,通常称这 个假想的定轴轮系为周转轮系的转化机构。 以单排2K-H型周转轮系为例 1 3 3 1 3 1 1 3 ( 1) Z Z i H H H H H = − − − = =