
Lecture 4 Solve of the Conduction Eq
Solve of the Conduction Eq. Lecture 4

Energy Conservation Equation Control Volume E 中年·”年… E ut 它 En+E。-Eom=dEu/dt=Eu Ey =pVCp dT Eg =gmet+ge
Energy Conservation Equation in g out st Est E E E dE dt Control Volume Ein Eout E g Est dt dT Est VCp Eq q g met e

The rate of Inflow or outflow energy by conduction,convection,radiation dT qcod=-kA dx com =hA(Ts-T) grod =(Ts-Tsr)A
The rate of Inflow or outflow energy by conduction, convection, radiation dT q A dx cond k s hA(T T ) conv q 4 4 s sur qrad εσ(T T )A

How to use the Energy Conservation Equation? e Define appropriate control volume with the control surface Identify appropriate time basis Identify relevant energy processes Write conservation equation
• Define appropriate control volume with the control surface • Identify appropriate time basis • Identify relevant energy processes • Write conservation equation How to use the Energy Conservation Equation?
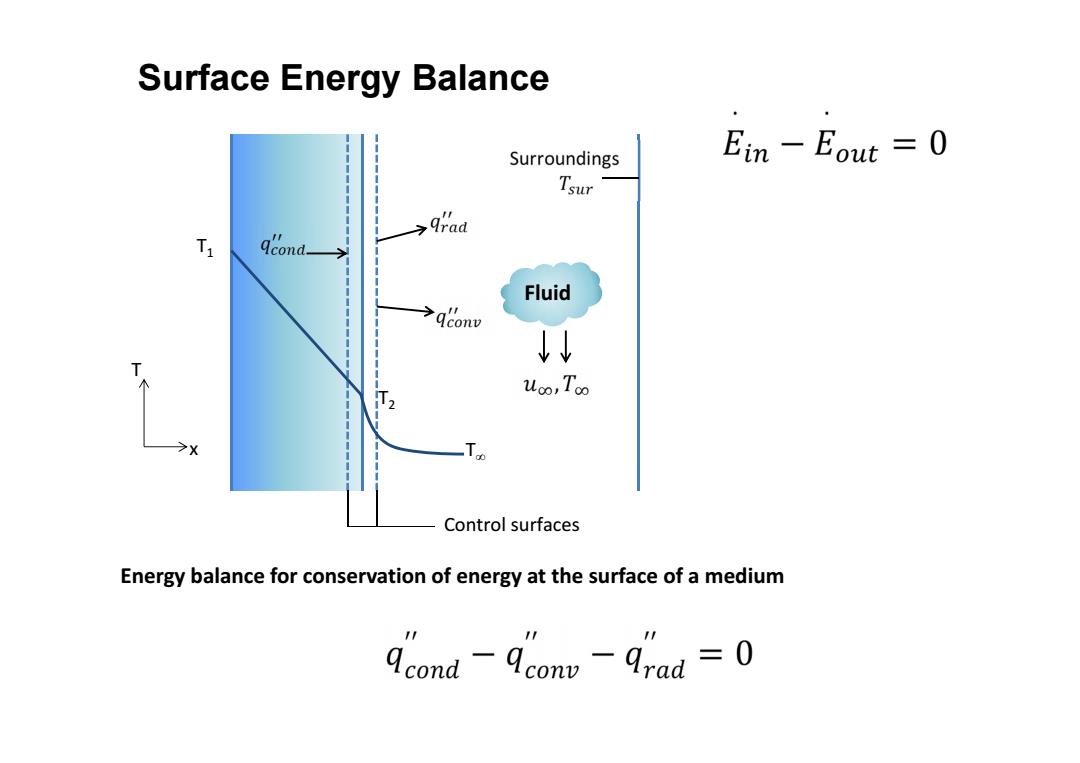
Surface Energy Balance Surroundings Ein-Eout =O Tsur 9raa qcond Fluid qconv T T2 uo,Too X Control surfaces Energy balance for conservation of energy at the surface of a medium dcond-dconv-Arad=0
Surface Energy Balance T1 T2 T x T ∞ Control surfaces Fluid Energy balance for conservation of energy at the surface of a medium

3D Conduction Eq. 0T=kV2T+9" PC In Cartesian coordinate systems: oC. T_
2 ''' p T C kTq t In Cartesian coordinate systems: 3D Conduction Eq. ( ) ( ) ( ) ''' p TT T T C k k kq txx yy z z

In Cylindrical coordinate systems: ++k+”=c at Y k a2T o2t aT In spherical coordinate systems: k 02T k∂ ot r2 Or sin0 0+r2sing 00 (sing +9 t pCp at
In Cylindrical coordinate systems: In spherical coordinate systems:

It is valid at every point in the material It is the heat equation for conduction in isotropic,constant conductivity material Further simplifications: ·Steady state ·One dimensional ·No energy generation
It is valid at every point in the material It is the heat equation for conduction in isotropic, constant conductivity material Further simplifications: Steady state One dimensional No energy generation

Boundary Conditions and Initial Conditions insulation 0 0 convection,h,T x
Boundary Conditions and Initial Conditions
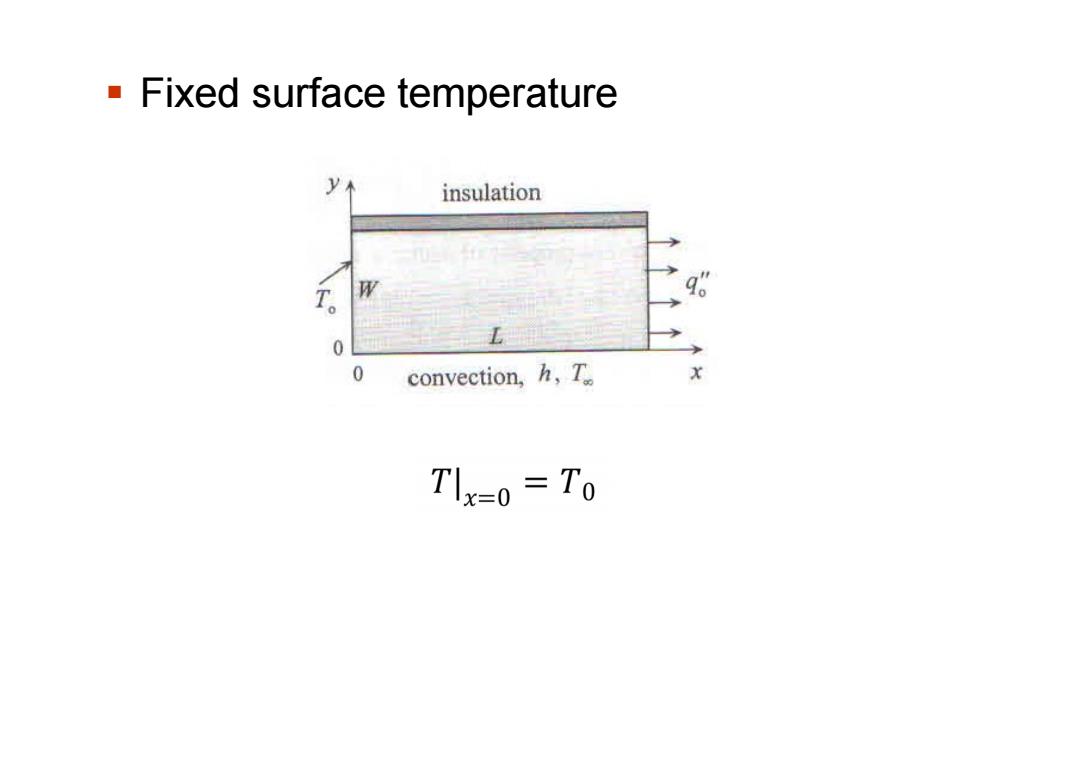
Fixed surface temperature insulation q 0 0 convection,h,T Tlx=0 To
Fixed surface temperature