
Lecture 3 Energy and Energy Conservation
Energy and Energy Conservation Lecture 3

Energy Conservation Equation Control Volume 中年·”年… g out E t En+Eg-Eou =dEs /dt =Est The rate at which thermal and mechanical energy enters a control volume,minus that leaving out,plus the rate at which thermal energy is generated within the control volume,should equal the rate of increase of energy stored within the control volume
Energy Conservation Equation in g out st Est E E E dE dt The rate at which thermal and mechanical energy enters a control volume, minus that leaving out, plus the rate at which thermal energy is generated within the control volume, should equal the rate of increase of energy stored within the control volume. Control Volume Ein Eout E g Est

-Internal Energy,Storage Energy, E pVCpT+Elaten dT E=pr℃ dt ■ Specific heat,Co,the amount of energy a body stores for each degree increase in temperature,on a per unit mass basis KJ/(K.Kg)
Internal Energy, Storage Energy, dt dT Est VCp Specific heat, Cp , the amount of energy a body stores for each degree increase in temperature, on a per unit mass basis KJ /(K Kg) E VC T E st p latent
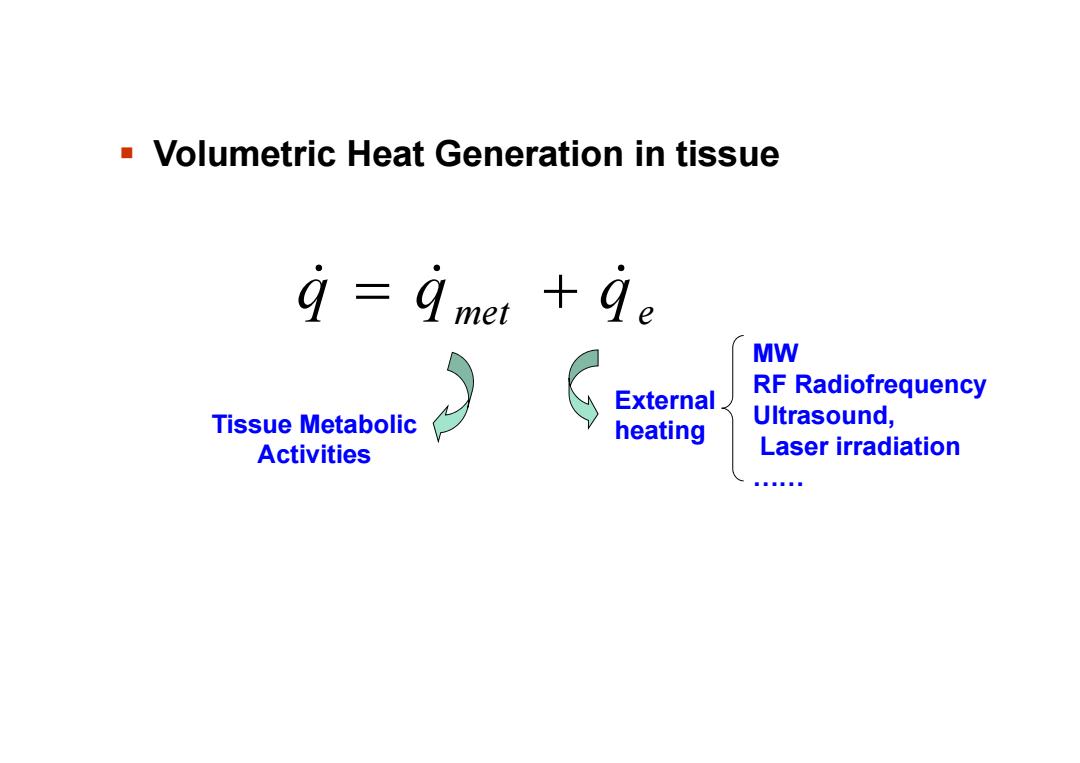
Volumetric Heat Generation in tissue q-gmet +ge MW External. RF Radiofrequency Tissue Metabolic heating Ultrasound, Activities Laser irradiation
q q met qe Tissue Metabolic Activities MW RF Radiofrequency Ultrasound, Laser irradiation …… External heating Volumetric Heat Generation in tissue

Energy inflow and outflow by conduction,convection,radiation
Energy inflow and outflow by conduction, convection, radiation

Conduction(Diffusion) a.Media:stationary solid,gas or liquid at diff b.Mechanism:molecular activities,free electrons or atomic vibrations c.Rate equ. (a))Heat current H Heat cument Ik Ti-Tc (b)Doubling the cross-sectional area of the conductor doubles the heat current (H is proportional to A). (c)Doubling the length of the conductor halves the heat current (is inversely proportional to L). Tc
Conduction (Diffusion) a. Media: stationary solid, gas or liquid at diff. b. Mechanism: molecular activities, free electrons or atomic vibrations c. Rate equ

Conduction across the surface: Rate equ. cond =-kA dT -Fourier's Law dx k--Thermal conductivity of the material [w/m.K]
Conduction across the surface: Rate equ. ——Fourier’s Law dT q A dx cond k k -- Thermal conductivity of the material [w/m·K]

qx--Heat transfer rate [w] k--Thermal conductivity of the material [w/m-K] A--Cross-sectional areaqx [m2] "means heat flowing from higher temperature to lower temperature dT =q”=-k [W/m2] A dx Heat flux =heat transfer rate/unit area
qx-- Heat transfer rate [w] k -- Thermal conductivity of the material [w/m·K] A -- Cross-sectional area ┴ qx [m2] “-” means heat flowing from higher temperature to lower temperature dx dT q Aq '' x x k [W/m2] Heat flux =heat transfer rate/ unit area

Convection a Media:between solid moving fluid b.Mechanism:Bulk motion effects c.Rate equ. q=hA(T、-Ta) Newton's law of cooling
Convection a Media: between solid & moving fluid b. Mechanism: Bulk motion effects c. Rate equ. Newton’s law of cooling hA(T T ) s q

h--Heat transfer coefficient [w/m2.k] Ts--Surface temperature T--Fluid temperature =q”=hT,-T) A
h -- Heat transfer coefficient [w/m 2·k] Ts -- Surface temperature T ∞ -- Fluid temperature h(T T ) A s '' q q