
Modeling in thermal treatment ------heating
Modeling in thermal treatment ‐‐‐‐‐‐heating

Predicting temp.distribution during hyperthermia 。Importance: -control of heating to provide sufficient thermal dose to tumor tissue but spare the surrounding healthy tissue (temp.elevation duration) -Technical difficulties of monitoring tissue temperature o Modeling: ot pc- =V.k,VT+(pc)p Wi (Ta-T)+gmb+gh t
Predicting temp. distribution during hyperthermia • Importance: – control of heating to provide sufficient thermal dose to tumor tissue but spare the surrounding healthy tissue (temp. elevation & duration) – Technical difficulties of monitoring tissue temperature • Modeling: ( ) ( ) t b b a mb h T c k T c wT T q q t
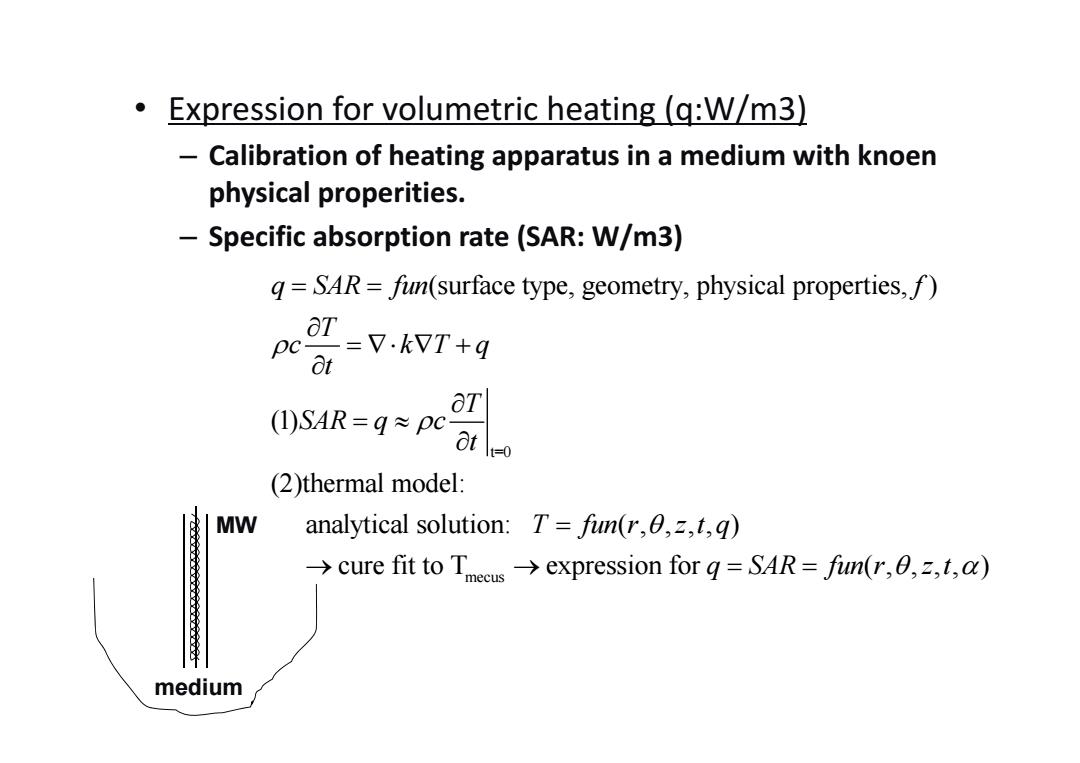
● Expression for volumetric heating(q:W/m3) - Calibration of heating apparatus in a medium with knoen physical properities. -Specific absorption rate (SAR:W/m3) g=SAR=fin(surface type,geometry,physical properties,f) =V.kWT+q pc 8t aT (SAR=g≈pcat (2)thermal model: MW analytical solution:T=fun(r,0,z,t,q) >cure fit to Tmeeusexpression for q=SAR=fin(r,,t,) medium
• Expression for volumetric heating (q:W/m3) – Calibration of heating apparatus in a medium with knoen physical properities. – Specific absorption rate (SAR: W/m3) t=0 mecus (surface type, geometry, physical properties, ) (1) (2)thermal model: analytical solution: ( , , , , ) cure fit to T expression for q SAR fun f T c kT q t T SAR q c t T fun r z t q q S AR fun r z t ( , , , , ) medium MW
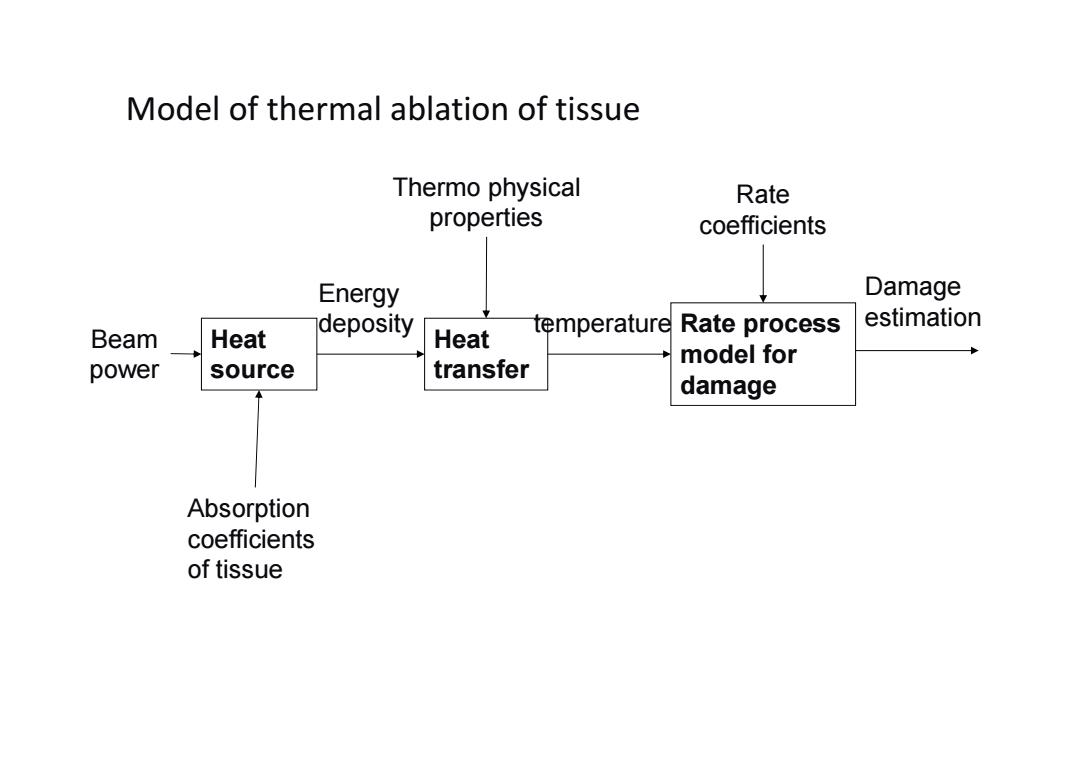
Model of thermal ablation of tissue Thermo physical Rate properties coefficients Energy Damage estimation Beam Heat deposity Heat temperature Rate process model for power source transfer damage Absorption coefficients of tissue
Model of thermal ablation of tissue Damage Rate process estimation model for q rzt n (, ,) damage Heat source Heat transfer Beam power Absorption coefficients of tissue Energy deposity Thermo physical properties temperature Rate coefficients T rzt (, ,) (, ) r z

。Difficulties: Thermal properties tumor type(cell morphology) P,c,k,~inisotropic temp.history dependent (heat shock proteins-HSP formation) 6*10*-0.22mW/cm',based on oxygen consumption Sien&Jain,1979 w(t.r)-s tumor type stage of the tumor Complex and dynamic geometry of tumor
• Difficulties: – Thermal properties – Complex and dynamic geometry of tumor b tumor type (, ) stage of the tumor w tr tumor type(cell morphology) , , inisotropic temp. history dependent (heat shock proteins-HSP formation) t c k 4 3 6 10 0.22 / , based on oxygen consumption Sien&Jain,1979 mb q mW cm

Mechanisms of heat induced damage Cytoplasmic and nuclear protein denaturation DNA and RNA changes and cellular membrane function change Tissue necrosis,coagulation and vaporization of tissue Damage degree function of tissue temperature and treatment time
Mechanisms of heat induced damage • Cytoplasmic and nuclear protein denaturation • DNA and RNA changes and cellular membrane function change • Tissue necrosis, coagulation and vaporization of tissue Damage degree : function of tissue temperature and treatment time
The thermodynamics of heat inactivation Life of a cell sustained by various metabolic activities rough ribosome endoplasmic mitochondrion reticulum plasma -o membrane cytoplasm microtubules (part of cytoskeleton) 9 lysosome nucleus smooth nucleolus endoplasmic chromatin reticulum nuclear pore nuclear envelope free ribosome Golgi complex centriole
The thermodynamics of heat inactivation Life of a cell sustained by various metabolic activities

Death caused by accumulation of inactivation of n different reactions and inactivation of chromosomal proteins the damage of each reaction or protein inactivation follows Arrhenius function =k, YT-AGIRT e dt h
Death caused by accumulation of inactivation of n different reactions and inactivation of chromosomal proteins the damage of each reaction or protein inactivation follows Arrhenius function G RT / s d T k e dt h

o--the total damage k.the rate of damage y--the Boltzmann's constant,1.38X 10-23 J/K h--the Planck's constant,6.63x10-34 J-s △G-the Gibbs free energy of inactivation △G=△H-T△S 4s--the entropy of inactivation (cal/K/mole) 4H--the enthalpy of the inactivation An approximate expression for k k,=2.05×(10)l0×T×e4s2×eaH/27
ω --the total damage ks – the rate of damage γ-- the Boltzmann’s constant, 1.38× 10−23 J/K h -- the Planck’s constant, 6.6310‐34 J‐s ΔG --the of inactivation Δs -- the entropy of inactivation (cal/K/mole) ΔH-- the enthalpy of the inactivation ΔG =ΔH‐TΔs Gibbs free energy 10 /2 /2 2.05 (10) s HT s k Te e An approximate expression for ks

Gibbs free energy a thermodynamic potential that measures the "useful"or process-initiating work obtainable from an isothermal,isobaric thermodynamic system. the chemical potential that is minimized when a system reaches equilibrium at constant pressure and temperature A convenient criterion of spontaneity for processes with constant pressure and temperature
the chemical potential that is minimized when a system reaches equilibrium at constant pressure and temperature A convenient criterion of spontaneity for processes with constant pressure and temperature a thermodynamic potential that measures the "useful" or process‐initiating work obtainable from an isothermal, isobaric thermodynamic system. Gibbs free energy